Question Based On Euclid Geometry

What Are The 5 Postulates Of Euclid’s Geometry

Euclid’s 5 postulates are:

• A straight line segment can be drawn for any two given points.
• A line segment can be extended in either direction to form a line.
• To describe a circle with any center and radius.
• All right angles are equal to one another.
• If two lines are intersected by a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines will intersect each other on that side if produced indefinitely.

Modern Standards Of Rigor

Placing Euclidean geometry on a solid axiomatic basis was a preoccupation of mathematicians for centuries. The role of primitive notions, or undefined concepts, was clearly put forward by Alessandro Padoa of the Peano delegation at the 1900 Paris conference:

…when we begin to formulate the theory, we can imagine that the undefined symbols are completely devoid of meaning and that the unproved propositions are simply conditions imposed upon the undefined symbols.

Then, the system of ideas that we have initially chosen is simply one interpretation of the undefined symbols but..this interpretation can be ignored by the reader, who is free to replace it in his mind by another interpretation.. that satisfies the conditions…

Logical questions thus become completely independent of empirical or psychological questions…

The system of undefined symbols can then be regarded as the abstraction obtained from the specialized theories that result when…the system of undefined symbols is successively replaced by each of the interpretations…

Padoa, Essai d’une théorie algébrique des nombre entiers, avec une Introduction logique à une théorie déductive quelconque

That is, mathematics is context-independent knowledge within a hierarchical framework. As said by Bertrand Russell:

Such foundational approaches range between foundationalism and formalism.

What Are The Important Topics Covered In Class 9 Maths Ncert Solutions Chapter 5

NCERT Solutions Class 9 Maths Chapter 5 covers a brief history of geometry and its origin, a basic understanding of Euclids Geometry, its definitions, axioms, and postulates. NCERT solutions class 9 Maths Chapter 5 Introduction To Euclids Geometry is an excellent resource to cover all core topics with suitable examples and sample problems.

Also Check: What Is Synthesis In Chemistry

Very Long Answer Questions

Ques. Which of the following statements are true and which are false? Give reasons for your answers.

Ans: False

Explanation: Many, i.e., infinite lines can pass through a single point. And that is the correct statement. Hence, the statement that only one line can pass through a single point is false.

Ans: False

Explanation: Euclid’s first postulate says that there is a unique line that passes through two distinct points. Hence, this statement says that there are an infinite number of lines that pass through two distinct points is false. Because it contradicts the first postulate of Euclid.

Ans: True

Explanation: Euclid’s second Postulate says that a terminated line can be produced indefinitely. Hence, this statement saying a terminated line can be produced indefinitely on both sides is correct.

Ans: True

Explanation: To rationalize this, we will first consider two circles with the same radii. We can observe and analyze that, when we make the two circles overlap with each other, we will get a superimposed figure of the two circles. Hence, we can conclude that the radii of both the circles will also be equal as the two circles are equal.

Ans: True

Euclids Geometry Class 9 Mcqs Questions With Answers

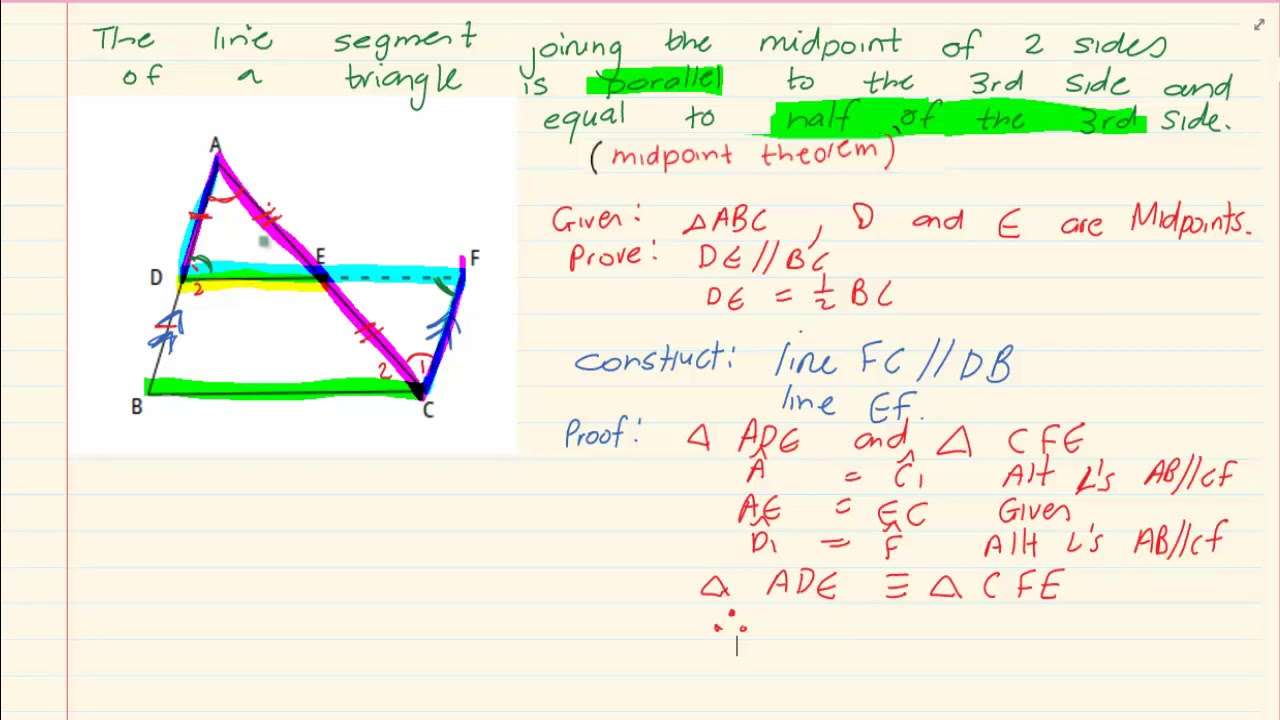
We have provided below chapter wise MCQs questions for Class 9 Euclids Geometry with answers which will help the students to go through the entire syllabus and and practice multiple choice questions provided here with solutions. As Euclids Geometry MCQs in Class 9 pdf download can be really scoring for students, you should go thorough all problems provided below so that you are able to get more marks in your exams.

Euclids Geometry Class 9 MCQ Questions

Our teachers have developed really good Multiple Choice Questions covering all important topics in each chapter which are expected to come in upcoming tests and exams, as MCQs are coming in all exams now therefore practice them carefully to get full understanding of topics and get good marks. Download the latest questions with multiple choice answers for Class 9 Euclids Geometry in pdf or read online for free.

The above NCERT based MCQs for Class 9 Euclids Geometry have been designed by our teachers in such a way that it will help you a lot to gain an understanding of each topic. These CBSE NCERT Class 9 Euclids Geometry Multiple Choice Questions have been developed and are available free for benefit of Class 9 students.

Advantages of Euclids Geometry Class 9 MCQ with Answers

a) MCQs will help the kids to strengthen concepts and improve marks in tests and exams.

Where can I get MCQs for Euclids Geometry?I want the latest MCQs based on this years syllabus ?

Read Also: How To Solve Acceleration In Physics

Cbse Chapter 5 Introduction To Euclids Geometry Hots Questions For Class 9

CBSE Board introduced questions based on – Higher Order Thinking Skills . The primary objective here was to improve the evaluating and analytical skills of a student. A lot of students tend to only focus on memorizing information and relying on cramming learning. Therefore CBSE Board decided to dedicate a large part of the question paper to Chapter 5 Introduction to Euclids Geometry HOTs Questions as they typically concentrate on a student’s ability to reason, analyze, process, justify, and evaluate information. Since a large part of CBSE question papers is based on HOTS, it is necessary for students to get ample practice with these questions. Experts at SelfStudys have compiled HOTs question for Class 9 for Science and Maths.

CBSE releases Chapter 5 Introduction to Euclids Geometry HOTs Questions for Class 9 every year. These papers are published prior to the examinations so that students can do the study. The students should practice Chapter 5 Introduction to Euclids Geometry HOTs Questions to increase perfection which will help him to get good marks in CBSE examination. Based on CBSE and NCERT guidelines same pattern as released every year.

Scaling Of Area And Volume

In modern terminology, the area of a plane figure is proportional to the square of any of its linear dimensions, A 3 } . Euclid proved these results in various special cases such as the area of a circle and the volume of a parallelepipedal solid. Euclid determined some, but not all, of the relevant constants of proportionality. E.g., it was his successor Archimedes who proved that a sphere has 2/3 the volume of the circumscribing cylinder.

Read Also: What Is Math Analysis In High School

Introduction To Euclid’s Geometry

• The number of dimensions a solid has:
• A.& nbsp

• Sample QuestionHow many sides does the triangle have?3

Important Questions & Solutions For Class 9 Maths Chapter 5

Q.1: What are the five postulates of Euclids Geometry?

Answer: Euclids postulates were:

Q.2: If a point C lies between two points A and B such that AC = BC, then prove that AC =1/2 AB. Explain by drawing the figure.

Solution:

Now, add AC on both sides.

L.H.S + AC = R.H.S + AC

Thus, we conclude that P and Q are the same points.

This contradicts our assumption that P and Q are two different midpoints of AB.

Thus, it is proved that every line segment has one and only one mid-point.

Hence Proved.

Q.4: In the given figure, if AC = BD, then prove that AB = CD.

Solution:

It is given, AC = BD

From the given figure, we get,

AC = AB + BC

BD = BC + CD

AB + BC = BC + CD

We know that, according to Euclids axiom, when equals are subtracted from equals, remainders are also equal.

Subtracting BC from the L.H.S and R.H.S of the equation AB + BC = BC + CD, we get,

AB + BC BC = BC + CD BC

AB = CD

Q.5: Does Euclids fifth postulate imply the existence of parallel lines? Explain.

Solution:

1+2=180°

Solution:

Also Check: Holt Mcdougal Pre Algebra Workbook

Ncert Solutions For Class 9 Maths Chapter 5 Introduction To Euclid Geometry Ex 52

Ex 5.2 Class 9 Maths Question 1.How would you rewrite Euclids fifth postulate so that it would be easier to understand?Solution:We can write Euclids fifth postulate as Two distinct intersecting lines cannot be parallel to the same line.

Ex 5.2 Class 9 Maths Question 2.Does Euclids fifth postulate imply the existence of parallel lines ? Explain.Solution:Yes. If a straight line l falls on two lines m and n such that sum of the interior angles on one side of l is two right angles, then by Euclids fifth postulate, lines m and n will not meet on this side of l. Also, we know that the sum of the interior angles on the other side of the line l will be two right angles too. Thus, they will not meet on the other side also. The lines m and n never meet, i.e, They are parallel.

Do I Need To Practice All Questions Provided In Ncert Solutions Class 9 Maths Introduction To Euclids Geometry

With a thorough practice of all the questions and sample problems listed in the NCERT Solutions Class 9 Maths Chapter 5, students can quickly gain an understanding of all the key notations. When students possess a sound knowledge of this topic, they can quickly implement the knowledge of the related topics. Practicing complete questions included in these solutions will also provide the necessary guidance and confidence to face various competitive exams.

You May Like: What Is Hydrostatic Pressure Biology

What Are The 7 Axioms Of Euclids

Axioms or common notions are theories made by Euclid that may or may not be used in geometry. The 7 axioms are:

Things that are equal to the same thing are equal to one another.

• If equals are added to equals, the wholes are equal.
• If equals are subtracted from equals, the remainders are equal.
• Things that coincide with one another are equal to one another.
• The whole is greater than the part.
• Things that are double of the same things are equal to one another.
• Things that are halves of the same things are equal to one another.

Very Short Answer Questions

Ques. Which of these statements is not in line with Euclids axiom?

Ans: Option d) is the correct answer.

Explanation: The statement is given in option d) says the whole is lesser than the part. But, the whole can never be lesser than the part. In fact, parts make the whole and if we divide the whole then it is parts. So, the whole is never less than the part. Hence, option d is the right answer.

Ques. Which of the following statements are true?

Ans: Option c) is the correct answer.

Explanation: Every other statement except the statement given in option c is false. Because a single point can be crossed or passed by many lines. Similarly, when two circles are equal, then, their radii are also equal, instead of being unequal. But, a terminated line can be produced indefinitely on both sides. Hence, option c is the correct answer.

Ques. If a line is drawn from the center of the circle to any point on its circumference. Then, this line is called:

Ans: Option c) is the correct answer.

Ans:

Recommended Reading: Hawkes Learning Systems Prealgebra And Introductory Algebra Answers

Complementary And Supplementary Angles

Angles whose sum is a right angle are called complementary. Complementary angles are formed when a ray shares the same vertex and is pointed in a direction that is in between the two original rays that form the right angle. The number of rays in between the two original rays is infinite.

Angles whose sum is a straight angle are supplementary. Supplementary angles are formed when a ray shares the same vertex and is pointed in a direction that is in between the two original rays that form the straight angle . The number of rays in between the two original rays is infinite.

Th Century And Relativity

Einstein’s theory of special relativity involves a four-dimensional space-time, the Minkowski space, which is non-Euclidean. This shows that non-Euclidean geometries, which had been introduced a few years earlier for showing that the parallel postulate cannot be proved, are also useful for describing the physical world.

However, the three-dimensional “space part” of the Minkowski space remains the space of Euclidean geometry. This is not the case with general relativity, for which the geometry of the space part of space-time is not Euclidean geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees due to gravity. A relatively weak gravitational field, such as the Earth’s or the Sun’s, is represented by a metric that is approximately, but not exactly, Euclidean. Until the 20th century, there was no technology capable of detecting these deviations in rays of light from Euclidean geometry, but Einstein predicted that such deviations would exist. They were later verified by observations such as the slight bending of starlight by the Sun during a solar eclipse in 1919, and such considerations are now an integral part of the software that runs the GPS system.

Read Also: What Does C Mean In Math

Introduction To Euclids Geometry Class 9 Mcqs Questions With Answers

Question 1.The number of dimensions, a solid has: 1

The total number of propositions in the elements are: 465

Answer: 465

Question 3.In Indus valley civilisation , the bricks used for construction work were having dimensions in the ratio 1 : 3 : 4

Answer: 4 : 2 : 1

Question 4.The things which are double of same thing are equal halves of same thing unequal double of the same thing

Which of the following statements is incorrect? A line segment has definite length. Three lines are concurrent if and only if they have a common point. Two lines drawn in a plane always intersect at a point. One and only one line can be drawn passing through a given point and parallel to a given line.

Answer: Two lines drawn in a plane always intersect at a point.

Question 6. Only one line can pass through a single point. Only one line can pass through two distinct points. A terminated line can be produced indefinitely on both the sides. If two circles are equal, then their radii are equal.

Answer: Only one line can pass through a single point.

Question 7.Which one of the following statements is true? Only one line can pass through a single point. There are an infinite number lines which pass through two distinct points. Two distinct lines cannot have more than one point in common. If two circles are equal, then their radii are not equal.

Answer: Two distinct lines cannot have more than one point in common.

Ncert Solutions For Class 9 Maths Chapter 5 Introduction To Euclid Geometry Ex 51

Ex 5.1 Class 9 Maths Question 1.Which of the following statements are true and which are false? Give reasons for your answers. Only one line can pass through a single point. There are an infinite number of lines which pass through two distinct points. A terminated line can be produced indefinitely on both the sides. If two circles are equal, then their radii are equal. In figure, if AB PQ and PQ = XY, then AB = XY.Solution: FalseReason : If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passingthrough O.

FalseReason : In the following figure, there are many straight lines passing through P. There are many lines, passing through Q. But there is one and only one line which is passing through P as well as Q.

TrueReason: The postulate 2 says that A terminated line can be produced indefinitely.

TrueReason : Superimposing the region of one circle on the other, we find them coinciding. So, their centres and boundaries coincide.Thus, their radii will coincide or equal.

TrueReason : According to Euclids axiom, things which are equal to the same thing are equal to one another.

Parallel Lines:Two lines l and m in a plane are said to be parallel, if they have no common point and we write them as l m.

Perpendicular Lines:Two lines p and q lying in the same plane are said to be perpendicular if they form a right angle and we write them as p q.

You May Like: How To Calculate Period Physics