What Is Simple Pendulum
A simple pendulum is defined as the mass that is suspended from a rod. A straight vertical line passing through the fixed position is the pendulum mean position.
The important points about the simple pendulum are listed here:
- The distance between the centre of mass to the point of suspension is called the length of the pendulum and it is denoted by L.
- The oscillatory motion of a simple pendulum is the to and fro motion of the pendulum periodically and the mid-point of the oscillation is the equilibrium.
- The time taken by the pendulum to complete one full oscillation is called the time period of the simple pendulum and it is denoted by T.
- The amplitude of a simple pendulum is the distance travelled by the pendulum from one side to the equilibrium position.
The formulas to compute the simple pendulum period and frequency are provided below:
T = 2 ×
= 2 x 3.14 x 1.23
= 7.769
f = 1/7.769
= 0.128
Therefore, the ime period and frequency of simple pendulum is 7.769 seconds and 0.128 oscillations per second.
Not only Simple Pendulum Calculator you can also get other physics calculators on our site Physicscalc.Com to solve your physics problems at a faster pace while doing assignments or homeworks.
Dynamics Of Simple Harmonic Oscillation
Visualizing Simple Harmonic Motion: Graphs of x,v, and a versus t for the motion of an object on a spring. The net force on the object can be described by Hooke’s law, and so the object undergoes simple harmonic motion. Note that the initial position has the vertical displacement at its maximum value X v is initially zero and then negative as the object moves down and the initial acceleration is negative, back toward the equilibrium position and becoming zero at that point.
Frequently Asked Questions On Orbital Period Calculator
1. How to calculate the orbital period of a binary star system?
To find the binary star system orbital period, you have to know the semi-major axis, first & second bodies mass. Divide the cube of the axis by the product of gravitational constant & sum of masses. Get the square root of the result with 2 to check the binary star orbital period.
2. What is Kepler’s third law formula?
Kepler’s 3rd law states that the square of the period is proportional to the cube of the semi-major axis of the orbit. Its formula is T = ).
3. What are the types of orbits?
There are different types of orbits, they are low earth orbit, transfer orbits, medium earth orbit, geostationary transfer orbit and sun-synchronous orbit.
4. What are the factors that affect the satellite orbital period?
The factor that affects the orbital period of a satellite is the central body density. By increasing the central body density, the orbital period value decreases.
Favorite Calculators
Read Also: Exponent Rules Worksheet 2 Answers
How To Calculate Simple Pendulum Period
The simple instructions to calculate the simple pendulum time period and frequency are mentioned here.
- Get the acceleration due to gravity and length of the pendulum.
- Divide the length by acceleration due to gravity and apply square root to the result.
- Multiply the value obtained in above step by 2 is called the time period.
- The reciprocal of time period is the frequency of the pendulum.
The Relationship Between Wave Frequency Period Wavelength And Velocity
Since wave frequency is the number of waves per second, and the period is essentially the number of seconds per wave, the relationship between frequency and period is
just as in the case of harmonic motion of an object. We can see from this relationship that a higher frequency means a shorter period. Recall that the unit for frequency is hertz , and that 1 Hz is one cycleâor one waveâper second.
The speed of propagation vw is the distance the wave travels in a given time, which is one wavelength in a time of one period. In equation form, it is written as
From this relationship, we see that in a medium where vw is constant, the higher the frequency, the smaller the wavelength. See Figure 13.8.
Don’t Miss: Span Linear Algebra Definition
Period Of Oscillations In A Shm Calculator
The Period of Oscillations in a SHM Calculator will calculate:
| Normal View |
| Mass of the object attached on a spring kg |
| Spring constant N/m |
| Length of pendulum’s thread m |
| Gravitational field strength m/s2 |
| Archimedes constant |
| Period of spring calculation |
|---|
| Period of simple pendulum calculation |
| TP = 2 ×L/g |
| Period Of Oscillations In A Shm Calculator Input Values |
| Mass of the object attached on a spring kg |
| Spring constant N/m |
| Length of pendulum’s thread m |
| Gravitational field strength m/s |
| Archimedes constant |
Please note that the formula for each calculation along with detailed calculations are available below. As you enter the specific factors of each period of oscillations in a shm calculation, the Period Of Oscillations In A Shm Calculator will automatically calculate the results and update the Physics formula elements with each element of the period of oscillations in a shm calculation. You can then email or print this period of oscillations in a shm calculation as required for later use.
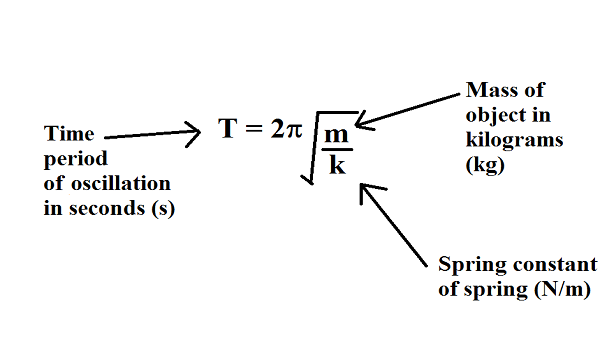
Vertical Motion And A Horizontal Spring
When a spring is hung vertically and a block is attached and set in motion, the block oscillates in SHM. In this case, there is no normal force, and the net effect of the force of gravity is to change the equilibrium position. Consider . Two forces act on the block: the weight and the force of the spring. The weight is constant and the force of the spring changes as the length of the spring changes.
Figure 15.9
. A mass is attached to the spring and a new equilibrium position is reached (
) when the force provided by the spring equals the weight of the mass. The free-body diagram of the mass shows the two forces acting on the mass: the weight and the force of the spring.
When the block reaches the equilibrium position, as seen in , the force of the spring equals the weight of the block,
The net force then becomes
This is just what we found previously for a horizontally sliding mass on a spring. The constant force of gravity only served to shift the equilibrium location of the mass. Therefore, the solution should be the same form as for a block on a horizontal spring,
The equations for the velocity and the acceleration also have the same form as for the horizontal case. Note that the inclusion of the phase shift means that the motion can actually be modeled using either a cosine or a sine function, since these two functions only differ by a phase shift.
Figure 15.10
Read Also: Kuta Software Infinite Algebra 2 Operations With Complex Numbers
How To Calculate The Period Of Motion In Physics
The natural world is full of examples of periodic motion, from the orbits of planets around the sun to the electromagnetic vibrations of photons to our own heartbeats.
All of these oscillations involve the completion of a cycle, whether it’s the return of an orbiting body to its starting point, the return of a vibrating spring to its equilibrium point or the expansion and contraction of a heartbeat. The time it takes for an oscillating system to complete a cycle is known as its period.
The period of a system is a measure of time, and in physics, it’s usually denoted by the capital letter T. Period is measured in time units appropriate for that system, but seconds are the most common. The second is a unit of time originally based on the rotation of the Earth on its axis and on its orbit around the sun, although the modern definition is based on vibrations of the cesium-133 atom rather than on any astronomical phenomenon.
The periods of some systems are intuitive, such as the rotation of the Earth, which is a day, or 86,400 seconds. You can calculate the periods of some other systems, such as an oscillating spring, by using characteristics of the system, such its as mass and spring constant.
When it comes to vibrations of light, things get a little more complicated, because photons move transversely through space while they vibrate, so wavelength is a more useful quantity than period.
Understanding The Restoring Force
Oscillating Ruler: When displaced from its vertical equilibrium position, this plastic ruler oscillates back and forth because of the restoring force opposing displacement. When the ruler is on the left, there is a force to the right, and vice versa.
restoring force
Restoring force, momentum, and equilibrium: The plastic ruler has been released, and the restoring force is returning the ruler to its equilibrium position. The net force is zero at the equilibrium position, but the ruler has momentum and continues to move to the right. The restoring force is in the opposite direction. It stops the ruler and moves it back toward equilibrium again. Now the ruler has momentum to the left. In the absence of damping , the ruler reaches its original position. From there, the motion will repeat itself.
You May Like: Who Is Paris Jacksons Mom
Period Of A Pendulum Equation
Surprisingly, for small amplitudes , the pendulum period doesn’t depend either on its mass or on the amplitude. It is usually assumed that “small angular displacement” means all angles between -15º and 15º. The formula for the pendulum period is
where:
- T is the period of oscillations – time that it takes for the pendulum to complete one full back-and-forth movement
- L is the length of the pendulum and
- g is the acceleration of gravity. On Earth, this value is equal to 9.80665 m/s² – this is the default value in the simple pendulum calculator.
You can find the frequency of the pendulum as the reciprocal of period:
How Is Frequency Formula Applied For The Given Values
The percentage formula is given as,
- The frequency formula in terms of time is given as: f = 1/T where, f is the frequency in hertz, and T is the time to complete one cycle in seconds
- The frequency formula in terms of wavelength and wave speed is given as, f = / where, is the wave speed, and is the wavelength of the wave
- The frequency formula in terms of angular frequency is given as, f = /2 where is the angular frequency
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
The Period And Wavelength Of A Wave
Like a simple oscillator, a wave has an equilibrium point and a maximum amplitude on either side of the equilibrium point. However, because the wave is traveling through a medium or through space, the oscillation is stretched out along the direction of motion. A wavelength is defined as the transverse distance between any two identical points in the oscillation cycle, usually the points of maximum amplitude on one side of the equilibrium position.
The period of a wave is the time it takes for one complete wavelength to pass a reference point, whereas the frequency of a wave is the number of wavelengths that pass the reference point in a given time period. When the time period is one second, frequency can be expressed in cycles per second and period is expressed in seconds.
The period of the wave depends on how fast it’s moving and on its wavelength . The wave moves a distance of one wavelength in a time of one period, so the wave speed formula is v = /T, where v is the velocity. Reorganizing to express period in terms of the other quantities, you get:
For example, if the waves on a lake are separated by 10 feet and are moving 5 feet per second, the period of each wave is 10/5 = 2 seconds.
Satellite Orbital Period Formula

Orbit is nothing but the path of a body that is revolving around a different object. Just like Earth orbits around the sun.
The orbital period is the time taken by an astronomical object to complete one orbit around the other object. In general, it applies to the planets, sun, moon, stars and many more. Kepler’s third law or Kepler’s laws planetary motion describes how a planet orbits around another.
The formula to calculate the orbital period of a satellite around the central body is T =
Where,
T is the orbital period
G is the gravitational constant
is the density of the central body
The binary star system has two stars that are close to each other and have similar masses that stars orbit around each other without a material central body. It has elliptical orbits.
The binary star system orbital period equation isTbinary = 2 *
Where,
M1 is the first body mass
M2 is the second body mass
a is the semi-major axis.
Example
Question: If the density of the earth is 5.21 g/cm³. What is the orbital period?
Solution:
Density of the earth = 5.21 g/cm³ = 5210 kg/m³
The formula of orbital period is T =
T =
= 1.445 hours
Therefore, the orbital period of earth is 1.445 hours
Avail free online calculators to learn physics, chemistry concepts from our website Physicscalc.Com. You will also get instant results by using our handy calculator tools.
You May Like: Find The Length Indicated
Oscilations Physics Tutorials Associated With The Uniform Motion Calculator
The following Physics tutorials are provided within the Oscilations section of our Free Physics Tutorials. Each Oscilations tutorial includes detailed Oscilations formula and example of how to calculate and resolve specific Oscilations questions and problems. At the end of each Oscilations tutorial you will find Oscilations revision questions with a hidden answer that reveals when clicked. This allows you to learn about Oscilations and test your knowledge of Physics by answering the test questions on Oscilations.
Frequently Asked Questions On Simple Pendulum Calculator
1. What are the applications of the simple pendulum?
The real-time applications of a simple pendulum are clock, wrecking ball, ballistic pendulum, bowling ball, Foucault’s pendulum, and metronome.
2. What are the three laws of the simple pendulum?
The following are the three laws of a pendulum.
3. What is the formula to compute the length of the pendulum?
The formula to find the length of the simple pendulum is L = /.
4. What is the oscillation in the pendulum?
Oscillation means a pendulum that moves from one extreme position to the other extreme position and returns to the starting position. The time to complete one oscillation is called the time period.
Favorite Calculators
Read Also: Geometry Basics Segment Addition Postulate
How To Calculate The Period Of The Movement From A Potential
I have an assignment, where I have an object moving in 1-D with a given mass and energy, and the potential V, and I’m supposed to calculate the period of the movement as a function of the energy $$V=\begin\infty & x < -a \\ 0 & -a < x < 0\\ \alpha x^2 & x> 0\end$$
Should I find 3 Lagrangians for the 3 separate parts of the potential? And then how would I come to the period of the movement? Thanks in advance!!
How Do You Calculate The Period And Frequency
#color(“Period ” = 1 / ” Frequency ” or ” T = 1 / f#
Explanation:
Frequency is the number of occurrences of a repeating event per unit of time.
It is also referred to as temporal frequency, which emphasizes the contrast to spatial frequency and angular frequency.
The period is the duration of time of one cycle in a repeating event, so the period is the reciprocal of the frequency.
Relationship between Period and frequency is as under :
The frequency of a wave describes the number of complete cycles which are completed during a given period of time.
As such, frequency is a rate quantity which describes the rate of oscillations or vibrations or cycles or waves on a per second basis.
A common unit of frequency is the Hertz, abbreviated as Hz.
#color(“Frequency ” = 1 / ” Period”#
Also Check: Theory Of Everything 2 All Coins
How To Analyze A Pendulum In Swing
Equations For A Simple Pendulum
The equations for a simple pendulum show how to find the frequency and period of the motion.
A simple pendulum consists of a point mass suspended on a string or wire that has negligible mass. If the pendulum weight or bob is pulled to a relatively small angle from the vertical and let go, it will swing back and forth at a regular period and frequency. These requirements allow for the equations to be relatively simple and are called simple harmonic motion.
If the bob is larger, the wire has mass, or the angle is larger, it is called a physical pendulum with complex equations of motion.
Although damping effects from air resistance and friction are a factor, they are considered negligible for the basic equations concerning the frequency or period of the pendulum.
Questions you may have include:
- What are the factors and parameters of pendulum motion?
- What are the equations for frequency and period?
- What are the equations for the length of the pendulum string?
This lesson will answer those questions. Useful tool: Units Conversion
Recommended Reading: Algebra 2 Simplifying Radicals With Variables Worksheet Answers