What About Indirect Measurements
If you are performing indirect measurements that require you to calculate your measurement results, then you should evaluate the equation used to determine your measurement result. Each variable in the equation will have its own uncertainty that will directly affect the uncertainty associated with the calculated measurement result.
To help you out, think of using dead weight testers or calibrating torque transducers and standard resistors. Each one of these measurement processes require you to use an equation to calculate a result for comparison purposes. To estimate uncertainty, you will want to break down the equation and evaluate the uncertainty of each variable in the equation.
;If you want to learn more about specifying the measurement function and process for your uncertainty analysis, check out this guide:
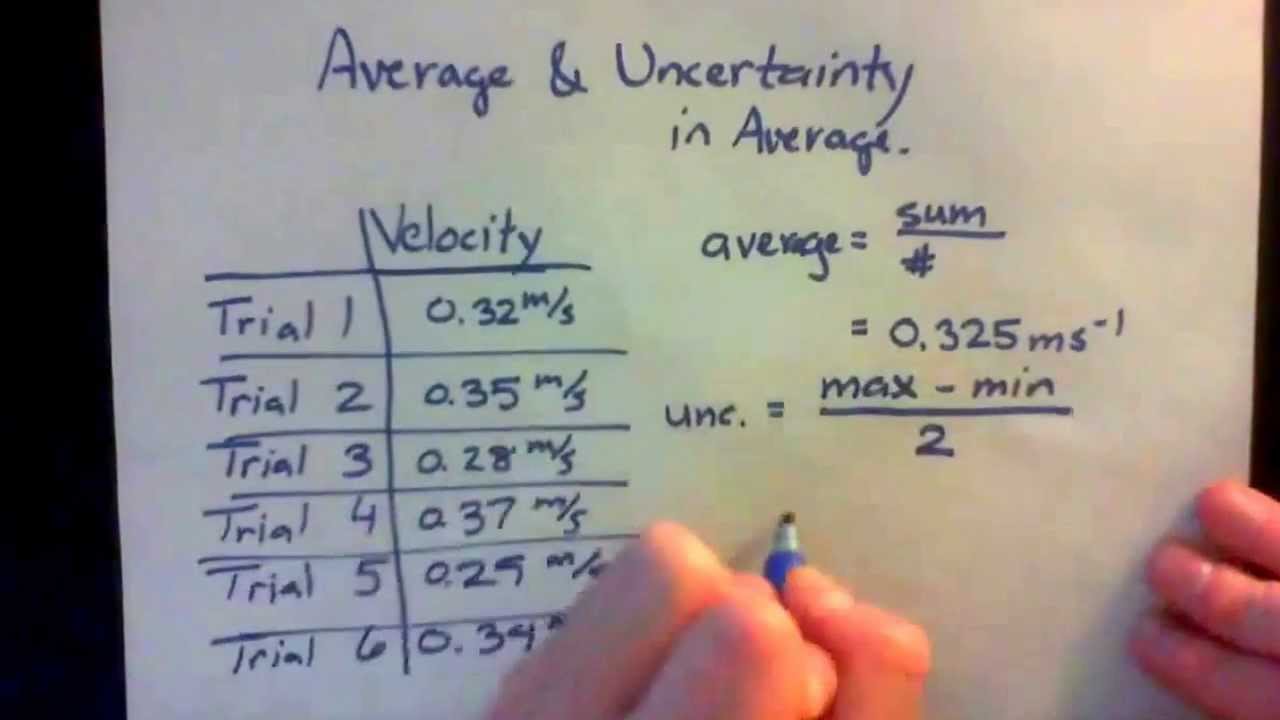
State Random Uncertainty As An Uncertainty Range And Represent It Graphically As An Error Bar
In IB physics, error bars only need to be used when the uncertainty in one or both of the plotted quantities are significant. Error bars are not required for trigonometric and logarithmic functions.
To add error bars to a point on a graph, we simply take the uncertainty range and draw lines of a corresponding size above and below or on each side of the point depending on the axis the value corresponds to.
Example:
Plot the following data onto a graph taking into account the uncertainty.
Table 1.2.1 – Distance vs Time data
Figure 1.2.2 – Distance vs. time graph with error bars;
In practice, plotting each point with its specific error bars can be time consuming as we would need to calculate the uncertainty range for each point. Therefor, we often skip certain points and only add error bars to specific ones. We can use the list of rules below to save time:
- Add error bars only to the first and last points
- Only add error bars to the point with the worst uncertainty
- Add error bars to all points but use the uncertainty of the worst point
- Only add error bars to the axis with the worst uncertainty
Mixtures Of Multiplication Division Addition Subtraction And Powers
If z is a function which involves several terms added or subtracted we must apply the above rules carefully.; This is best explained by means of an example.
Example:; w = cm, x = cm, y = cm. Find z = w x +y^2
z = wx +y^2 = 18.0
First we compute v = wx as in the example in to get v = . Finally, we compute Dz = Dv + D = 0.9 + 3.6 = 4.5 rounding to 4 We have v = wx = cm.; The calculation of the uncertainty in is the same as that shown to the left. Then from Eq. 1b; Dz =; 3.7 ;
Don’t Miss: What Is Mean Median Mode And Range In Math
How To Find Sources Of Uncertainty
To find sources of uncertainty for your analysis, follow steps listed below:
How To Calculate The Combined Uncertainty

To calculate the combined standard uncertainty, simply following these instructions:
To summarize the instructions above, simply square the value of each uncertainty source. Next, add them all together to calculate the sum . Then, calculate the square-root of the summed value . The result will be your combined standard uncertainty.
After you complete this process, you will have the combined standard uncertainty at a 1-sigma level characterized by a Normal distribution per the Central Limit Theorem.
Also Check: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Measurement Functions With Equations
If your measurement function includes equations, then the process to estimate uncertainty is a little different. You will want to identify each variable in the equation and think about what influences each variable.
For example, if you are evaluating the calibration of a torque transducer, you will first write out the equation.
When you evaluate the equation further, you begin to account for other factors that influence the equation. In this example, we begin to consider the radius of the torque arm and cable, the mass of the weights and pan, and the local gravity. If needed, we can evaluate the equation even further to account for more influences and increase the complexity of your uncertainty analysis.
Now that you have identified the equation and the variables, you can start to research what factors may cause changes or variations to each variable. Using the example above, think about how temperature variations can cause thermal linear expansion or contraction of the arm radius, and how it can affect air density which affects air buoyancy correction that can vary the magnitude of applied force.
As you can see, evaluating equations can help you find sources of uncertainty. While this process may seem easy, it can become quite difficult depending on the complexity of the equation. Knowing the rules for the propagation of uncertainty can come in handy in step 5.
Convert Uncertainty Components To Standard Deviation Equivalents
Once you select a probability distribution, you can identify the equation needed to convert each uncertainty contributor to a standard deviation equivalent. This will reduce each source of uncertainty to a 1-sigma level , so you can properly combine them using the GUM method in the next step.
Make sure to perform this task for each uncertainty contributor that you quantified in step 3.
Also Check: Write The Segment Addition Postulate For The Points Described
Root Sum Of Squares Method
If you are a more visual learner, like me, take a look at the process below to see if it makes more sense.
Below, you will see the equation for calculating the combined uncertainty.
This is the equation that I typically use since I usually include sensitivity coefficients earlier in the process before I convert uncertainty components to standard deviations.
If you evaluate measurement uncertainty the same way, you should be able to use the simplified equation. If you do not use sensitivity coefficients at all, you can use the simplified equation as well.
Both equations give you the same result. So, use the equation that works best for you. If you are using an excel spreadsheet calculator, you may find the function in the next section beneficial.
Describe And Give Examples Of Random And Systematic Errors
Random errorsA random error, is an error which affects a reading at random.Sources of random errors include:
- The observer being less than perfect
- The readability of the equipment
- External effects on the observed item
Systematic errors
A systematic error, is an error which occurs at each reading.Sources of systematic errors include:
- The observer being less than perfect in the same way every time
- An instrument with a zero offset error
- An instrument that is improperly calibrated
You May Like: Holt Geometry Lesson 4.5 Practice B Answers
Example: Calculate The Standard Deviation With The Equation Above
The following measurements are given:
5.4 6.7 3.8 5.1 6.3
Step 1: Calculate the mean of all the measurements.
The number of measurements is N=5, so the mean is:
/ 5 = 5.46
Step 2: Calculate the square of each sample minus the mean.
^2 = 0.0036
^2 = 1.5376
^2 = 2.7556
^2 = 0.1296
^2 = 0.7056
Step 3: Sum all those squares for all measurements.
0.0036 + 1.5376 + 2.7556 + 0.1296 + 0.7056 = 5.132
Step 4: Divide the sum by N and take the square root.
Sqrt = 1.0131
We want to have the same number of decimal points as for the mean, so we round it to 2 decimal places: 1.01
Step 5: State the final measurement.
The final measurement is the mean +/- the standard deviation, so our answer is 5.46 +/- 1.01.
Here you can use an online tool to calculate the standard deviation.
Perform Arithmetic Operations With Uncertain Measurements
Recommended Reading: Geometry Segment Addition Postulate Worksheet
Estimating The Uncertainty In Measurements
Before you combine or do anything with your uncertainty, you have to determine the uncertainty in your original measurement. This often involves some subjective judgment. For example, if youre measuring the diameter of a ball with a ruler, you need to think about how precisely you can really read the measurement. Are you confident youre measuring from the edge of the ball? How precisely can you read the ruler? These are the types of questions you have to ask when estimating uncertainties.
In some cases you can easily estimate the uncertainty. For example, if you weigh something on a scale that measures down to the nearest 0.1 g, then you can confidently estimate that there is a ±0.05 g uncertainty in the measurement. This is because a 1.0 g measurement could really be anything from 0.95 g to just under 1.05 g . In other cases, youll have to estimate it as well as possible on the basis of several factors.
Tips
-
Significant Figures:Generally, absolute uncertainties are only quoted to one significant figure, apart from occasionally when the first figure is 1. Because of the meaning of an uncertainty, it doesnt make sense to quote your estimate to more precision than your uncertainty. For instance, a measurement of 1.543 ± 0.02 m doesnt make any sense, because you arent sure of the second decimal place, so the third is essentially meaningless. The correct result to quote is 1.54 m ± 0.02 m.
How To Evaluate Your Uncertainty Budget
To evaluate your expanded measurement uncertainty estimates, use one or more of the following methods listed below. Then, determine if your expanded uncertainty is reasonable and appropriate.
1. Evaluate the Significance of Uncertainty Contributors
For this evaluation, calculate the significance of each source of uncertainty and analyze how much it influences your total measurement uncertainty. Double-check uncertainty components with excessively large and small percentages to verify their value is correct.
4. Expanded Uncertainty vs SRM Certificate of Analysis
For this evaluation, review the Certificate of Analysis for the standard reference material that your reference standard is traceable to and verify your uncertainty is larger than the uncertainty of the SRM.
5. Expanded Uncertainty vs Other Labs (Option A
In this evaluation, compare your estimated uncertainty with other laboratories. Search your accreditation bodys database and look at 3 to 5 other laboratory scopes of accreditation to make sure that your expanded uncertainty is reasonably comparable. If not, you may have overestimated or underestimated uncertainty.
This option works best for calibration laboratories since their uncertainty published in their scopes of accreditation. This option is more difficult if you are a test lab. Most test labs do not report their test uncertainties in their scope of accreditation which makes it difficult to compare your capabilities with other laboratories.
Recommended Reading: Eoc Fsa Practice Test Answers
Calculating The Expanded Uncertainty
After finding your coverage factor , calculate the expanded uncertainty by multiplying the coverage factor and the combined standard uncertainty. Use the formula below for guidance.
The result is the expanded uncertainty . This is your uncertainty in measurement estimated to a 95% confidence interval.
Look at the image below to see the equation used in one of my uncertainty calculators.
Thats it! You have just learned how to calculate expanded uncertainty in 7 steps and completed the process for the estimation of uncertainty in measurement.
However, you are not done yet. I recommend that you verify your calculations and evaluate your results. In the next section, I will tell you how to evaluate uncertainty calculations for appropriateness.
To learn more about coverage factors and expanded uncertainty or making CMC Uncertainty equations for your scope of accreditation, click the links below:
How To Convert Uncertainty To Standard Deviations
To convert uncertainty components to standard deviations, follow the steps listed below:
Refer to the chart below to find the divisor associated with the probability distribution that you selected in step 4.
Next, divide your uncertainty components by the appropriate divisor to convert them to a standard uncertainty. Afterward, all of your contributors should be on the same confidence level and equivalent to a standard deviation.
Also Check: What Type Of Math Is On The Ged
State Units In The Accepted Si Format
There are several ways to write most derived units. For example: meters per second can be written as m/s or m s-1. It is important to note that only the latter,;m s-1, is accepted as a valid format. Therefor, you should always write meters per second as m s-1;and meters per second per second as m s-2. Note that this applies to all units, not just the two stated above.
The Uncertainty Of Measurements
measurementsuncertainty analysiserror analysistrue valuepreciseaccurateaccuracyprecisionAccuracyerrorPrecisionuncertaintyNote:erroruncertaintyaccuracyaccuracyaccuracyacceptedstandardprimary mass standardaccuraterelativefractional uncertaintym
Note:lessPrecisionAccuracyrandomsystematic
Also Check: Fsa Algebra 1 Eoc Review Functions And Modeling Answer Key
Selected Solutions To Problems & Exercises
1.; 57.9 m/s;; 9.55 × 109 eV;; From Table 1 in Photon Energies and the Electromagnetic Spectrum, we see that typical molecular binding energies range from about 1eV to 10 eV, therefore the result in part is approximately 9 orders of magnitude smaller than typical molecular binding energies.
3.;29 nm;;290 times greater
5.;1.10 × 1013 eV
7.;3.3 × 1022 s
9.;2.66 × 1046 kg
- College Physics. : OpenStax College. Located at: . License: CC BY: Attribution. License Terms: Located at License
Calculate The Combined Uncertainty
After converting your uncertainty sources to standard deviation equivalents, it is time to calculate the combined uncertainty using the root sum of squares method recommended in the Guide to the Expression of Uncertainty in Measurement .
This will mathematically combine your uncertainty sources in quadrature. So, keep reading to learn how to combine uncertainty.
Don’t Miss: What Is Figure Ground Perception Psychology
Determine The Uncertainties In The Gradient And Intercepts Of A Straight
GradientTo calculate the uncertainty in the gradient, we simply add error bars to the first and last point, and then draw a straight line passing through the lowest error bar of the one points and the highest in the other and vice versa. This gives two lines, one with the steepest possible gradient and one with the shallowest, we then calculate the gradient of each line and compare it to the best value. This is demonstrated in figure 1.2.3 below:
Figure 1.2.3 – Gradient uncertainty in a graph;
InterceptTo calculate the uncertainty in the intercept, we do the same thing as when calculating the uncertainty in gradient. This time however, we check the lowest, highest and best value for the intercept. This is demonstrated in figure 1.2.4 below:
Figure 1.2.4 – Intercept uncertainty in a graph
Note that in the two figures above the error bars have been exaggerated to improve readability.
Heisenberg Uncertainty For Energy And Time
There is another form of Heisenbergs uncertainty principle for simultaneous measurements of energy and time. In equation form, \Delta\Delta\ge\frac\\,;where E is the uncertainty in energy and t is the uncertainty in time. This means that within a time interval t, it is not possible to measure energy preciselythere will be an uncertainty E in the measurement. In order to measure energy more precisely , we must increase t. This time interval may be the amount of time we take to make the measurement, or it could be the amount of time a particular state exists, as in the next Example 2.
Recommended Reading: Draw The Lewis Structure For Ccl4
Calculate The Uncertainty Of Multiple Measurements