How To Solve Two
A two-column proof is only a structure, like a skeleton. You must have five tools handy to work your way from premise to conclusion and complete the two column proof:
What Is A Proof
A proof is a logical argument that tries to show that a statement is true. In math, and computer science, a proof has to be well thought out and tested before being accepted. But even then, a proof can be discovered to have been wrong. There are many different ways to go about proving something, well discuss 3 methods: direct proof, proof by contradiction, proof by induction. Well talk about what each of these proofs are, when and how theyre used.
Before diving in, well need to explain some terminology.
A theorem is a mathematical statement which is proven to be true.
A statement that has been proven true in order to further help in proving another statement is called a lemma.
Now that weve gotten that out of the way, lets job into some types of proofs!
Congruency Of Triangles: Asa Sss Sas Aas
-
States, if the two angles and the side included between them of one triangle are equal to the two corresponding angles and the side included between them of another triangle, the two triangles are congruent.
-
states, if the three sides of one triangle are equal to the three corresponding sides of another triangle, the two triangles are congruent.
-
says that If two sides and an included angle of one triangle are congruent to two corresponding sides and an included angle of another triangle, then the triangles are congruent.
-
States, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.
-
says that If two angles and non-included sides of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.
Read Also: Common Core Algebra 2 Unit 13 Lesson 9 Answers
How To Explain Different Types Of Proofs In Geometry
Face it: Proofs are not easy. And in geometry, things seem to get worse, as now you have to turn pictures into logical statements, making conclusions based on simple drawings. The different types of proofs you learn in school can be overwhelming at first. But once you understand each type, youll find it much easier to wrap your head around when and why to use different types of proofs in geometry.
What Is The Difference Between Prove And Proof
In fact, both words have similar meanings, the main difference between proof and prove is that proof is a noun while prove is a verb. Proof means the evidence or argument establishing a fact or the truth of a statement. Prove means demonstrating the truth or existence of something by evidence or argument.
What are the five elements that the deductive structure of a proof contain? Thus, as well as being an appropriate argument supported by valid reasoning, we also take a deductive proof to consist of the following components: singular propositions , universal propositions , and the appropriate
Is proof part of geometry?
A two-column geometry proof is a problem involving a geometric diagram of some sort. Youre told one or more things that are true about the diagram , and youre asked to prove that something else is true about the diagram .
What is the difference between theorem and postulate? The difference between postulates and theorems is that postulates are assumed to be true, but theorems must be proven to be true based on postulates and/or already-proven theorems.
Also Check: What Is Concentration Measured In Chemistry
Proof By Mathematical Induction
Despite its name, mathematical induction is a method of deduction, not a form of inductive reasoning. In proof by mathematical induction, a single “base case” is proved, and an “induction rule” is proved that establishes that any arbitrary case implies the next case. Since in principle the induction rule can be applied repeatedly , it follows that all cases are provable. This avoids having to prove each case individually. A variant of mathematical induction is proof by infinite descent, which can be used, for example, to prove the irrationality of the square root of two.
A common application of proof by mathematical induction is to prove that a property known to hold for one number holds for all natural numbers:Let N = be the set of natural numbers, and let P be a mathematical statement involving the natural number n belonging to N such that
- P is true, i.e., P is true for n = 1.
- P is true whenever P is true, i.e., P is true implies that P is true.
- Then P is true for all natural numbers n.
For example, we can prove by induction that all positive integers of the form 2n â 1 are odd. Let P represent “2n â 1 is odd”:
The shorter phrase “proof by induction” is often used instead of “proof by mathematical induction”.
What Are The Three Basic Types Of Geometry
There are three basic types of geometry: Euclidean, hyperbolic and elliptical. Although there are additional varieties of geometry, they are all based on combinations of these three basic types. Euclidean geometry is the original form, dating back to 300 BC, and it is the result of the work of the Greek Alexandrian mathematician Euclid, who developed the five postulates, or axioms, upon which his geometric theorems are built.
Euclids fifth postulate, known as the parallel postulate, went without an accompanying proof for thousands of years. The parallel postulate assumes that a straight line crossing through two other straight lines and forming two same-side interior angles of less than 90 degrees determines that those two lines, if extended far enough, will eventually meet on the side of the interior angles. This assumption, however, did not take into account the idea of curved space, which was first conceptualized by Albert Einstein in his 1915 General Theory of Relativity.
The idea of space existing with either a positive or a negative curvature introduced the idea of non-Euclidean geometry, in which the parallel postulate would not always hold true. In curved space, it cannot be assured that the two lines in question will ever meet, regardless of how far they might be extended. The geometry based on space with a negative curvature became known as hyperbolic geometry. Elliptical geometry refers to the type of geometry based on space with a positive curvature.
Also Check: Trek Madone 9.9 Geometry
What Harm Does It Do When Proofs Are Removed
Limiting the amount of substantial and challenging proofs in a geometry curriculum pretty much defeats the purpose of the course.Geometrical proofs offer students a clear introduction to logical arguments, which is central to all mathematics. They show the exact relationship between reason and equations.
Undecidability Consistency And Metamathematics
As I mentioned at the beginning of this story, Kurt Gödel discovered a remarkable fact about logical systems.
Gödel proved two theorems now known as Gödels Incompleteness Theorems. The first one can be stated informally as
First Incompleteness Theorem ~ Kurt Gödel.
Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete i.e., there are statements of the language of F which can neither be proved nor disproved in F.
It is hard to grasp how huge a blow it must have been for the many hopeful mathematicians back then. Not just because of the annoying implication that there are truths out there we will never prove, but also because what if say the Riemann hypothesis is such a statement? Then all the theorems that depend on it will be thrown out and there will always be a limit as to how much knowledge we can get on the distribution of the prime numbers not to mention: how much time and energy should we put into this particular pursuit if we dont know if it is a decidable problem within our axiomatic system?
Second Incompleteness Theorem ~ Kurt Gödel.
Assume F is a consistent system which contains elementary arithmetic. Then it is not possible to prove that F is consistent within F.
This is much worse than the first theorem!
It says that we will never know if the system we are working in is consistent. What do we mean by consistent?
But we will never be sure about that, Gödel says.
Now, you might be thinking:
Recommended Reading: What Is Condensed Matter Physics
Referencesisbn Links Support Nwe Through Referral Fees
- Enderton, H.B. 2000. A Mathematical Introduction to Logic, Second edition. Academic Press. ISBN 0122384520
- Solow, D. 2004. How to Read and Do Proofs: An Introduction to Mathematical Thought Processes. Wiley. ISBN 0471680583
- Troelstra, A. S. and H. Schwichtenberg. 2000. Basic Proof Theory, Second edition. Cambridge University Press. ISBN 978-0521779111
- Velleman, D. 2006. How to Prove It: A Structured Approach. Cambridge University Press. ISBN 0521675995
The Three Most Helpful Geometric Proofs
Much of geometry is about working backwards in order to solve problems. Unlike other types of math, in geometry youre often given the answer to a problem and asked to demonstrate how its true. In order to do this, you must utilize geometric proofs.
Geometric proofs are a list ofStatementsandReasons used to prove that a given mathematical concept or idea is true.
Statements are claims about a geometric problem that cannot be proven true until backed by a mathematical Reason.
Reasons are pieces of evidence that support a Statement.
Today we will demonstrate how to write a proof using columns, boxes, and paragraphs. Each method provides a different way to list the steps and show why each Statement is true. So here is a breakdown of three of the most useful geometric proofs, how and when to use them, and why knowing them will make geometry so much easier!
Two-Column Proofs
Two-column proofs are a type of geometric proof made up of two columns. The first has a list of Statements. The second has a list of Reasons that correlate to each Statement.
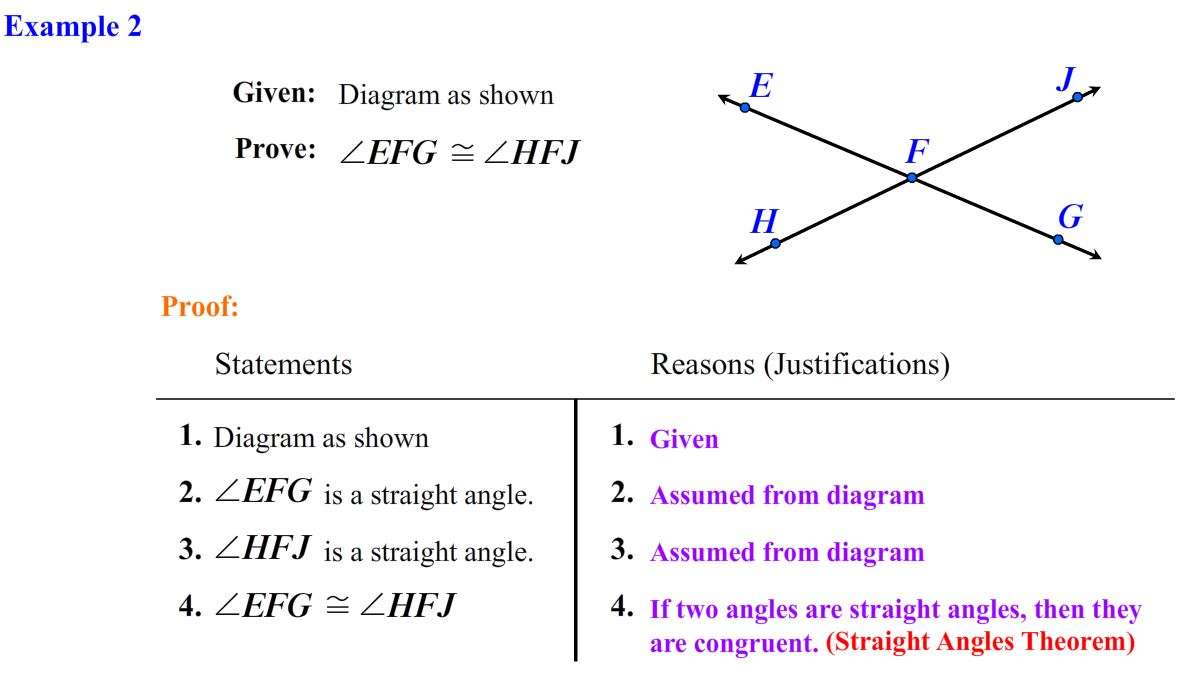
This picture shows angles A, B, and C.
Its given that C and A are complementary, meaning that when you add them together they equal 90°. Its also given that B and C are complementary.
Now we must prove that angles A and B are equal.
| Statements | |
|
|
Definition of Congruent Angles |
Paragraph Proofs
Using what we know about Paragraph Proofs, lets evaluate the problem below
Flowchart Proof
Best Practices for Geometric Proofs
Don’t Miss: Algebra Math Problems For 8th Graders
Formal And Informal Proofs
In general, a proof is a demonstration that a specified statement follows from a set of assumed statements. The specified statement that follows from the assumed statements is called the conclusion of the proof and the assumed statements that the conclusion follows from are called the premises of the proof.
In mathematics, proofs are often expressed in natural language with some mathematical symbols. These type of proofs are called informal proof. A proof in mathematics is thus an argument showing that the conclusion is a necessary consequence of the premises, i.e. the conclusion must be true if all the premises are true. When all the premises of proofs are statements that have been previously agreed on for the purpose of the study in a given mathematical field, which are called axioms, the conclusions of such proofs are called theorems.
On the other hand, in logic, a proof is formally meant to be a sequence of formulas in some deductive system that shows the transformation from the set of premises into the conclusion by the rules specified in the deductive system . When all the premises of proofs are axioms in the deductive system, i.e. the formulas syntactically specified in the deductive system, the conclusions of proofs are called theorems as in mathematics. Proof theory studies this notion of proof as its subject matter.
How Is Mathematics Built
In this little story, I will go over some of the most used proof techniques and try to make it clear how to really prove things in mathematics.
Along the way, I will give you examples to solidify the theory and to show you some of the beauty of the reasoning involved.
If you ask a pure mathematician what mathematics is really about, there is a strong likelihood that the answer is going to be something along the lines mathematics is about proving theorems or gaining knowledge.
For many people, doing mathematics is almost equivalent to trying to come up with proofs of theorems.
However, if you ask me, I think that mathematics is more than that. If you catch me in a philosophical mood, I would probably say something like
Mathematics is a tool for some, an art for others, a universal and timeless language of nature itself, an adventurous expedition into uncharted waters of natural facts, a global culture and a tenacious pursuit of truth and pure knowledge.
But thats me
Before we get started we need to cover the basics. In our case, we need to think about mathematical truth and how it all fits together.
The first thing to realize about a proof is that it depends on other truths. These truths come in two variants: proved statements, typically called theorems, and something called axioms.
An axiom is a statement that is assumed true and that doesnt require a proof. You can view axioms as the atoms of mathematics because all other things are build from them.
Also Check: Geometry 3.5 Worksheet Answers
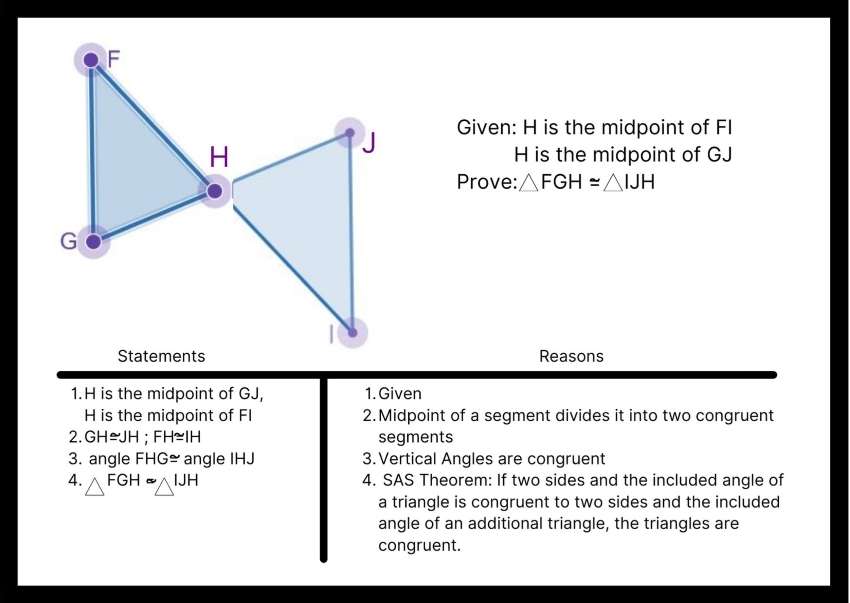
How Do You Prove A Paragraph Proof
I will have angles with same measure, so that makes that the lines must be parallel. Okay, the proof is ready in my mind now. PROOF WRITTEN IN TWO-COLUMN FORM:
| Argument | |
|---|---|
| 6. The angles A and A are congruent. | 6. They are vertical angles. |
| 7. The angles A and A are congruent. | 7. 5 and 6 together. |
What does a paragraph proof look like? Paragraph proofs are comprehensive paragraphs that explain the process of each proof. Like two-column proofs, they have multiple steps and justifications. But instead of columns, the given information is formatted like a word problem written out in long-hand format.
Three Types Of Geometric Proofs You Need To Know
Geometric proofs are given statements that prove a mathematical concept is true. In order for a proof to be proven true, it has to include multiple steps. These steps are made up of reasons and statements.
There are many types of geometric proofs, including two-column proofs, paragraph proofs, and flowchart proofs. Well walk you through each type.
You May Like: How To Figure Out Area In Math
Articles Which Mention Dependencies Of Theorems
- This page was last edited on 10 July 2022, at 03:16 .
- Text is available under the Creative Commons Attribution-ShareAlike License 3.0 additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.
Sound Overwhelming Read This For Help:
| If proofs intimidate you as a new Geometry teacher, or even if youre a veteran and your kids always struggle through the first weeks of proofs, you are not alone! Its such a tricky new way of thinking for them. But dont skip them! Instead, go about it in a better way. Check out this twist: Its a key step that I added into my introductory unit on proofs for a much smoother transition into teaching proof writing. It made a world of difference for my students.I wrote up this post to guide you through a smoother way to set students up for success with proof writing. Click the image to |
| Looking for even more support? The complete unit I developed includes a presentation and printables to lead your students from the basics , through a special revamped Algebra proof that scaffolds their learning all the way up through writing their first batch of Geometry proofs! This method is the smoothest way to introduce this challenging unit. Check out what’s included in the full unit. |
Also Check: How To Solve Commission Math Problems
How Do You Make A Proof
The Structure of a Proof
What is a proof in design? A proof is a preliminary version of a printed piece, intended to show how the final piece will appear. Proofs are used to view the content, color and design elements before committing the piece to copy plates and press.
What are proofs in writing?
16 2 Page 3 1 What does a proof look like? A proof is a series of statements, each of which follows logically from what has gone before. It starts with things we are assuming to be true. It ends with the thing we are trying to prove. So, like a good story, a proof has a beginning, a middle and an end.
Why are proofs important in geometry? Geometrical proofs offer students a clear introduction to logical arguments, which is central to all mathematics. They show the exact relationship between reason and equations. More so, since geometry deals with shapes and figures, it opens the students brains to visualizing what must be proven.