For Function Graphs And Tables
#1: Start by finding the $\bi y$-intercept
Generally, the easiest place to begin when working with functions is by finding the $y$-intercept. From there, you can often eliminate several different answer choices that do not match our graph or our equation .
The $y$-intercept is almost always the easiest piece to find, so it’s always a good place to begin.
#2: Test your equation against multiple ordered pairs
It is always a good idea to find two or more points of your functions and test them against a potential function equation. Sometimes one ordered pair works for your graph and a second does not.
You must match the equation to the graph that works for every coordinate point/ordered pair, not just one or two.
Four Ways To Represent A Function
- Page ID
- 4434
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Advantages Of Using Function Notation
- Since most functions are represented with various variables such as a, f, g, h, k etc., we use f in order avoid confusion as to which function is being evaluated.
- Function notation allows to identify the independent variable with ease.
- Function notation also helps us to identify the element of a function which has to be examined.
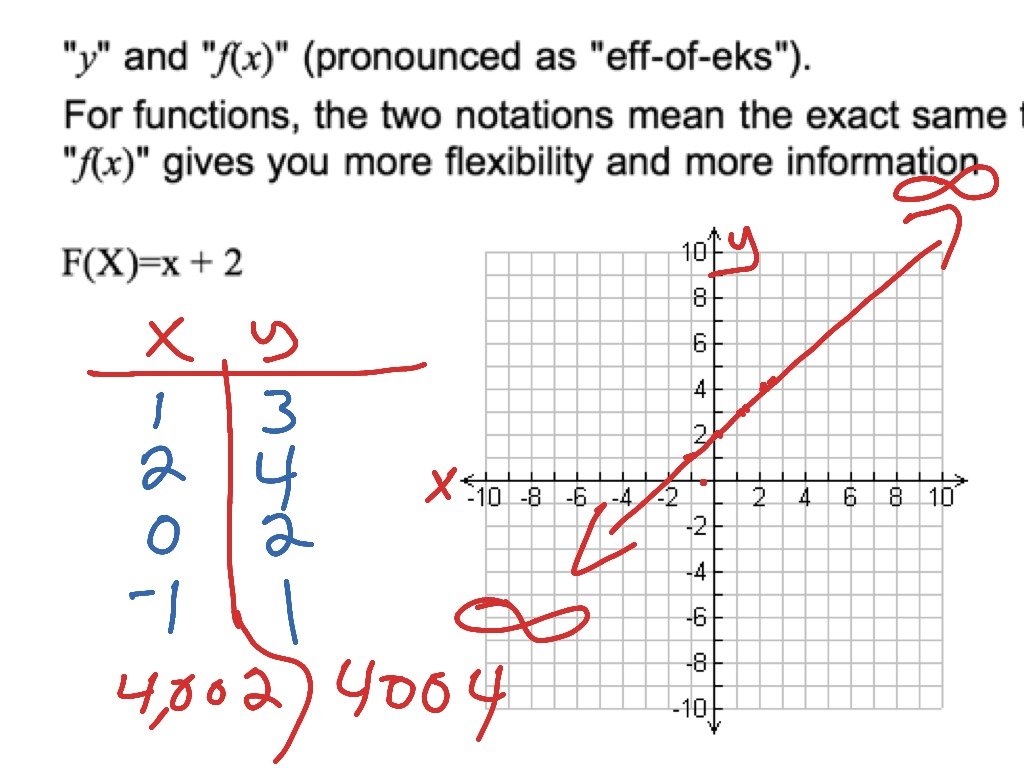
Consider a linear function y = 3x + 7. To write such function in function notation, we simply replace the variable y with the phrase f to get
f = 3x + 7. This function f = 3x + 7 is read as the value of f at x or as f of x.
Read Also: Valence Electrons In Ccl4
Example: Finding An Equation Of A Function
Express the relationship 2n+6p=12 as a function p=f\left, if possible.
To express the relationship in this form, we need to be able to write the relationship where p is a function of n, which means writing it as p= expression involving n.
\begin& 2n+6p=12\\ & 6p=12 – 2n & & \text2n\text. \\ & p=\frac & & \text. \\ & p=\frac-\frac \\ & p=2-\fracn \end
Therefore, p as a function of n is written as
p=f\left=2-\fracn
Analysis of the Solution
It is important to note that not every relationship expressed by an equation can also be expressed as a function with a formula.
Watch this video to see another example of how to express an equation as a function.
Finding Input And Output Values Of A Function
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the functions formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Recommended Reading: Ccl4 Lewis Dot
Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship other times, the table provides a few select examples from a more complete relationship.
Table \ lists the input number of each month , \, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year . Note that, in this table, we define a days-in-a-month function \ where \\) identifies months by an integer rather than by name.
|
Month number, \ |
Finding The Domain Of A Function With A Square Root
Don’t Miss: What Does Abiotic Mean In Biology
What Makes A Relation A Function
On the other hand, a function is actually a special kind of relation because it follows an extra rule. Just like a relation, a function is also a set of ordered pairs however, every x-value must be associated to only one y-value.
Suppose we have two relations written in tables,
- A relation that is not a function
Since we have repetitions or duplicates of x-values with different y-values, then this relation ceases to be a function.
- A relation that is a function
This relation is definitely a function because every x-value is unique and is associated with only one value of y.
So for a quick summary, if you see any duplicates or repetitions in the x-values, the relation is not a function. How about this example though? Is this not a function because we have repeating entries in x?
Be very careful here. Yes, we have repeating values of x but they are being associated with the same value of y. The point shows up twice, and while the point is written three times. This table can be cleaned up by writing a single copy of the repeating ordered pairs.
The relation is now clearly a function!
How To: Given A Function In Equation Form Write Its Algebraic Formula
Don’t Miss: What Is Figure Ground Perception Psychology
Finding The Domain Of A Function Using A Relation
What Is A Function Notation
Notation can be defined as a system of symbols or signs that denote elements such as phrases, numbers, words etc.
Therefore, function notation is a way in which a function can be represented using symbols and signs. Function notation is a simpler method of describing a function without a lengthy written explanation.
The most frequently used function notation is f which is read as f of x. In this case, the letter x, placed within the parentheses and the entire symbol f, stand for the domain set and range set respectively.
Although f is the most popular letter used when writing function notation, any other letter of the alphabet can also be used either in upper or lower case.
Recommended Reading: What Are Two Types Of Elastic Forces
Express The Problem Question Or Statement
In Algebra word problems, the problem is expressed as either a question or a statement.
Question:
- How many trees will John have to plant?
- How many televisions will Sara have to sell to earn $50,000?
Statement:
- Find the number of trees John will have to plant.
- Solve for the number of televisions Sara will have to sell to earn $50,000.
Sharpening Your Algebra Skills
- x +2 = 3
- + =
- At this point, we’ll subtract 2 from both sides by simply removing 2 boxes from both sides:
- +- =-
Recommended Reading: Geometry Dash Demon Key Hack
What Is A Function
In mathematics, a function is a set of inputs with a single output in each case. Every function has a domain and range. The domain is the set of independent values of the variable x for a relation or a function is defined. In simple words, the domain is a set of x-values that generate the real values of y when substituted in the function.
On the other hand, the range is a set of all possible values that a function can produce. The range of a function can be expressed in interval notation or inform of inequalities.
For Function Equations And Nested Equations
#1: Always work inside out
Nested functions can look beastly and difficult, but take them piece by piece. Work out the equation in the center and then build outwards slowly, so as not to get any of your variables or equations mixed up.
#2: Remember to FOIL
It is quite common for ACT to make you square an equation. This is because many students get these types of questions wrong and distribute their exponents instead of squaring the entire expression.
If you don’t properly FOIL, then you will get these questions wrong. Whenever possible, try not to let yourself lose points due to these kinds of careless errors.
Ready to test your function knowledge?
Now let’s put our function knowledge to the test, using real ACT math problems.
1. A function $f$ is defined as $f=-8x^2$. What is $f$?
F. -72
Our final answer is A, -70.
Congrats! You’ve mastered ACT functions!
Recommended Reading: Can Work Be Negative Physics
Using The Vertical Line Test
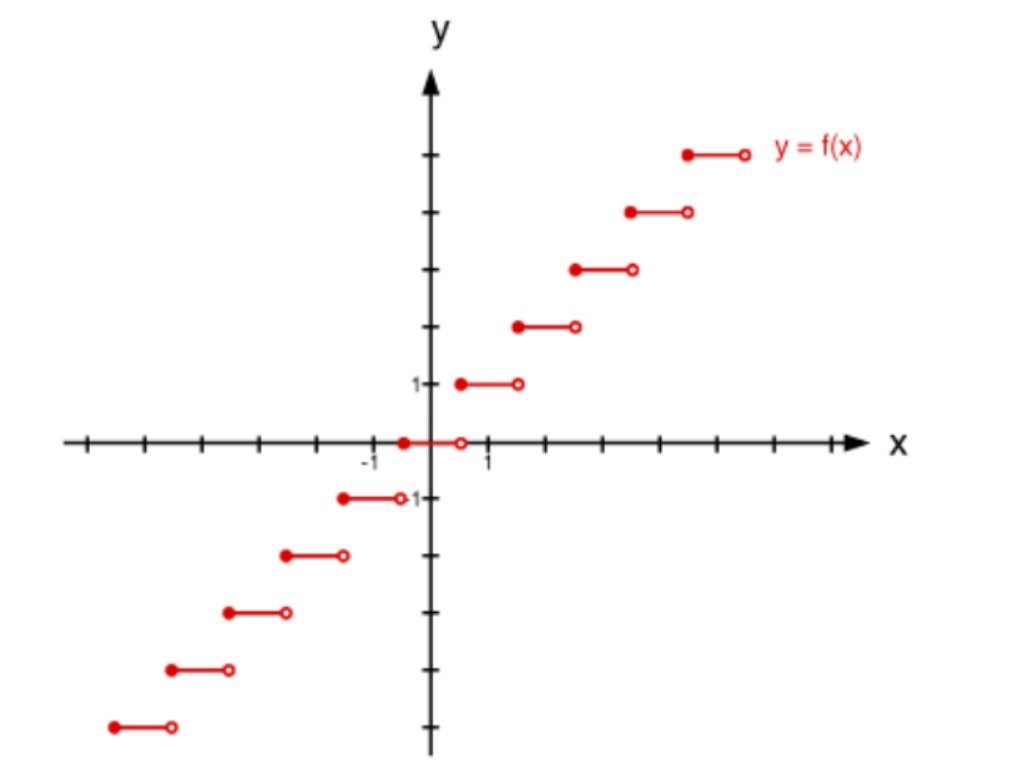
As we have seen in some examples above, we can represent a function using a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value \ and the output \, and we say \ is a function of \, or \\) when the function is named \. The graph of the function is the set of all points \\) in the plane that satisfies the equation \\). If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. For example, the black dots on the graph in Figure \ tell us that \=2\) and \=1\). However, the set of all points \\) satisfying \\) is a curve. The curve shown includes \\) and \\) because the curve passes through those points
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. See Figure \.
Howto: Given a graph, use the vertical line test to determine if the graph represents a function
Example \: Applying the Vertical Line Test
The Role Of Complex Numbers
From an algebraic perspective, complex numbers enter quite naturally into the study of algebraic functions. First of all, by the fundamental theorem of algebra, the complex numbers are an algebraically closed field. Hence any polynomial relation p = 0 is guaranteed to have at least one solution for y at each point x, provided we allow y to assume complex as well as real values. Thus, problems to do with the domain of an algebraic function can safely be minimized.
yyxyx
Furthermore, even if one is ultimately interested in real algebraic functions, there may be no means to express the function in terms of addition, multiplication, division and taking nth roots without resorting to complex numbers . For example, consider the algebraic function determined by the equation
- y
, }},} the square root is not real, and one has to choose, for the square root, either non-real square root. Thus the cubic root has to be chosen among three non-real numbers. If the same choices are done in the two terms of the formula, the three choices for the cubic root provide the three branches shown, in the accompanying image.
It may be proven that there is no way to express this function in terms of nth roots using real numbers only, even though the resulting function is real-valued on the domain of the graph shown.
- 1
- d y =}\oint _}y}}\,dy}
which is an analytic function.
Recommended Reading: Paris Jackson Biological Mother
How Do You Identify A Simple Function
1 Expert Answer The simple function is the absolute value function y = |x|. Since the 9 is on the outside of the absolute value with the x, it affects the vertical shift. More specifically, the on the outside shifts the graph of y =|x| down 9 units. The simple function is the square root function y = x.
Evaluating A Function Given In Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppys memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours.
The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See the table below.
| Pet | |
|---|---|
| Beta fish | 3600 |
At times, evaluating a function in table form may be more useful than using equations. Here let us call the function P.
The domain of the function is the type of pet and the range is a real number representing the number of hours the pets memory span lasts. We can evaluate the function P at the input value of goldfish. We would write P\left=2160. Notice that, to evaluate the function in table form, we identify the input value and the corresponding output value from the pertinent row of the table. The tabular form for function P seems ideally suited to this function, more so than writing it in paragraph or function form.
Recommended Reading: Paris Jackson’s Parents
As An Element Of A Cartesian Product Over A Domain
The set of all functions from some given domain to a codomain is sometimes identified with the Cartesian product of copies of the codomain, indexed by the domain. Namely, given sets X and Y, any function f: X â Y is an element of the Cartesian product of copies of Ys over the index set X
- f â âXY = YX.
Viewing f as tuple with coordinates, then for each x â X, the xth coordinate of this tuple is the value f â Y. This reflects the intuition that for each x â X, the function picks some element y â Y, namely, f.
Infinite Cartesian products are often simply “defined” as sets of functions.
Evaluating And Solving Functions
- Evaluate and solve functions in algebraic form.
- Evaluate functions given tabular or graphical data.
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function f\left=5 – 3^ can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
Read Also: Which Founding Contributors To Psychology Helped Develop Behaviorism
Evaluating Functions Expressed In Formulas
Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form. For example, the equation \ expresses a functional relationship between \ and \. We can rewrite it to decide if \ is a function of \.
How to: Given a function in equation form, write its algebraic formula.
Example \: Finding an Equation of a Function
Express the relationship \ as a function \\), if possible.
Solution
To express the relationship in this form, we need to be able to write the relationship where \ is a function of \, which means writing it as \.
Therefore, \ as a function of \ is written as
Analysis
It is important to note that not every relationship expressed by an equation can also be expressed as a function with a formula.
Example \: Expressing the Equation of a Circle as a Function
Does the equation \ represent a function with \ as input and \ as output? If so, express the relationship as a function \\).
Solution
-
\=\dfrac}\)
Q & A