How To Find Range In Math

What Are The Rules To Find The Domain Of A Function

Here are some general rules used to find domain of different types of functions:

• f = polynomial, the domain is the set of all real numbers.
• f = 1/x, domain if the set of all real numbers but x0.
• f = x, domain if the set of all real numbers such that x 0.
• f = ln x, domain is the set of all real numbers such that x > 0.

Domain And Range From Graph

It is very easy to find the domain and range of a function if its graph is given/known. The set of values of x covered by the graph gives the domain and the set of values of y covered by the graph gives the range. But keep a note of the following things while writing the domain and range from a graph.

• See whether the graph passes the vertical line test. Otherwise, it is not a function and we do not usually define domain and range for such curves.
• If there is any hole on the graph, then its coordinates shouldn’t be in the domain and range.
• If there is a vertical asymptote, then the corresponding value of x shouldn’t be there in the domain.
• If there is a horizontal asymptote, then the corresponding value of x shouldn’t be there in the range.
• If the graph is broken into pieces, then we get multiple sets/intervals in the domain and range and we club all such sets/intervals by “union” symbol .
• If there is an arrow at the end of a curve, then it means that the curve is supposed to be extended infinitely in that particular direction.

Here is an example of a graph and we will find the domain and range from the graph.

In the above graph:

• All the x-values from – to are covered by the graph . Hence, the domain = .
• All the y-values greater than or equal than or equal to 0 are covered by the graph . Hence, the range = [0, ).

Important Notes on Domain and Range:

Related Topics:

What Will I Learn From This Article

After reading this article, you will be able to:

• properly define the range in statistics
• solve for the range of ungrouped data
• solve for the range of a frequency table
• determine the range in a histogram
• determine the range in a boxplot
• determine the range in a scatterplot
• interpret the range of data
• know the limitations of using range given a data set and
• properly determine when to use the range.

You May Like: What Does It Mean To Evaluate In Math

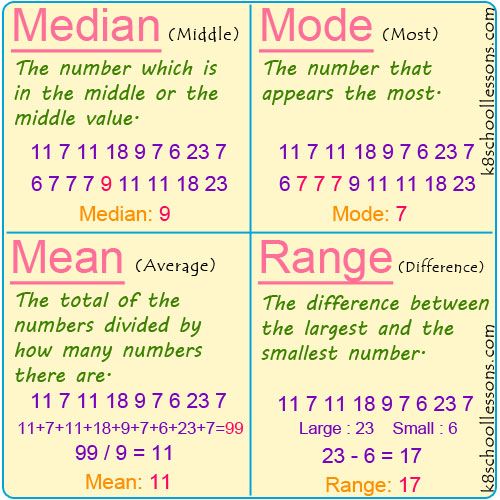
How To Find The Range In Math

How to Find the Range in Math?

The Range is the difference between the lowest and highest values.

Example: In the lowest value is 3, and the highest is 9.

So the range is 9 3 = 6.

It is that simple!

But perhaps too simple

STRUGGLING WITH MATH? Get the assistance, on-going support and tutors you need to learn faster, make fewer mistakes and get the grades you deserve. Learn More.

Domain And Range Of A Function

The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and the range is the possible output given by the function.

If there exists a function \ such that every element of \ is mapped to elements in \, then \ is the domain, and \ is the co-domain. The image of an element \ under a relation \ is given by \, where \ R\). The range of the function is the set of images. The domain and range of a function is denoted in general as follows: Domain \ = \) and range \=\).

The domain and range of this function \ = 2x\) is given as domain \ , range \.

Don’t Miss: Algebra 1 Solving Systems Of Equations By Substitution Worksheet

Finding The Range Of A Function In A Word Problem

Finding The Range Of A Function Given A Formula

You May Like: How Are Physical And Human Geography Alike

What Is The Domain And Range Of A Function

The domain and range of a function are the set of all the inputs and outputs a function can give respectively. The domain and range are important aspects of a function. The domain takes all the possible input values from the set of real numbers and the range takes all the output values of the function.

More Domain And Range Examples

In case you missed it earlier, you can see more examples of domain and range in the section Inverse Trigonometric Functions.

We fire a ball up in the air and find the height h, in metres, as a function of timet, in seconds, is given by

h = 20t 4.9t2

Find the domain and range for the functionh.

Answer

Generally, negative values of time do not have any meaning. Also, we need to assume the projectile hits the ground and then stops – it does not go underground.

So we need to calculate when it is going to hit the ground. This will be when h = 0. So we solve:

20t 4.9t2 = 0

Also Check: Geometry Dash Blast Processing Full Ver

Finding The Domain Of A Function Defined By An Equation

In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.

We can visualize the domain as a holding area that contains raw materials for a function machine and the range as another holding area for the machines products ).

We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket \). We will discuss interval notation in greater detail later.

Before we begin, let us review the conventions of interval notation:

• The smallest term from the interval is written first.
• The largest term in the interval is written second, following a comma.
• Parentheses, \ or \\), are used to signify that an endpoint is not included, called exclusive.
• Brackets, \, are used to indicate that an endpoint is included, called inclusive.

Finding Domains And Ranges Of The Toolkit Functions

We will now return to our set of toolkit functions to determine the domain and range of each.

For the constant function\=c\), the domain consists of all real numbers there are no restrictions on the input. The only output value is the constant \, so the range is the set \ that contains this single element. In interval notation, this is written as \, the interval that both begins and ends with \.

Figure \: Identity function f=x.

For the identity function \=x\), there is no restriction on \. Both the domain and range are the set of all real numbers.

For the absolute value function \=|x|\), there is no restriction on \. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.

For the quadratic function \=x^2\), the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.

For the cubic function \=x^3\), the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.

Figure \: Square root function \=\sqrt\).

For the cube root function \=\sqrt\), the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative .

Read Also: How To Study For The Acs General Chemistry 1 Exam

Upper And Lower Medians

Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.

Omit the centermost value.

Find the median of the lower portion.

Calculate the average of the two values.

The median of the lower portion is

Find the median of the upper portion.

Calculate the average of the two values.

The median of the upper potion is

If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.

Find the median of the lower portion.

The median of the lower portion is two.

Find the median of the upper portion.

The median of the upper portion is eight.

Find The Range Of A Function Relation Of Ordered Pairs

A relation is the set of ordered pairs i.e., the set of where the set of all x values is called the domain and the set of all y values is called the range of the relation.

In the previous chapter, we have learned how to find the domain of a function using relation.

Now we learn how to find the range of a function using relation.

For that we have to remember 2 rules which are given below:

Rules:

Now see the examples given below to understand this concept:

Example 20: Find the range of the relation

Solution:

In the relation , the set of x coordinates is and the set of y coordinates is .

If we draw the diagram of the given relation it will look like this

Here we can clearly see that each element of the set is related to a unique element of the set .

Therefore the given relation is a Function.

Also, we know that the range of a function relation is the set of y coordinates.

Therefore the range of the relation is the set .

Example 21: Find the range of the set of ordered pairs

Solution:

The diagram of the given relation is

Here we can see that element 9 is related to two different elements and they are 4 and 13 i.e., 9 is not related to a unique element and this goes against the definition of the function.

Therefore the relation is not a Function.

Don’t Miss: What Are The Major Specialties In Psychology

For Continuous Iid Random Variables

For nindependent and identically distributed continuous random variablesX1, X2, …, Xn with the cumulative distribution function G and a probability density function g, let T denote the range of them, that is, T= max-min.

The range, T, has the cumulative distribution function

F . ^g^\,}x.}

Gumbel notes that the “beauty of this formula is completely marred by the facts that, in general, we cannot express G by G, and that the numerical integration is lengthy and tiresome.”:385

If the distribution of each Xi is limited to the right then the asymptotic distribution of the range is equal to the asymptotic distribution of the largest value. For more general distributions the asymptotic distribution can be expressed as a Bessel function.

The mean range is given by

n G ^x\,}G}

where x is the inverse function. In the case where each of the Xi has a standard normal distribution, the mean range is given by

^)^-\Phi ^)\,}x.}

When To Use The Range

If an intuitive statistic is needed

The range is an excellent metric when a straightforward statistic indicating the degree of data dispersion is required. Everybody understands the concept of maximum and lowest data points.

Rapid assessment

Additionally, when you require a rapid assessment, it is simple to calculate in your head utilizing summary statistics.

Small data sets

When working with tiny datasets and comparing samples of similar size, use the range to avoid outliers.

Detecting data entry problems

It is a remarkable statistic for detecting data entry problems. Due to its susceptibility to outliers, a single error can appear.

It can be used to solve standard deviation

The range can be used to calculate another type of spread, the standard deviation. Rather than going through a very lengthy procedure, we may simply use what is known as the range rule to determine the standard deviation. The range plays a critical role in this calculation.

Using for quality control

Quality control analysts frequently use this particular metric of variability. To begin, if the range of a batch of items exceeds the spread between the higher and lower specification limits, they know that at least one component is out of specification.

For instance, if the range of part lengths is 10 mm, but the spread for specification limits is 5 mm, there must be some parts that are not within specification.

Recommended Reading: Can My Husband Adopt My Child Without Biological Father’s Consent

Find The Range Of A Logarithmic Function

The range of any logarithmic function is .

We can verify this fact from the graph.

f=\log_x^ is a logarithmic function and the graph of this function is

Here you can see that the y value starts from -\infty and extended to +\infty,

i.e., the range of f=\log_x^ is .

Example 19: Find the range of the logarithmic function

f=\log_+3

Solution:

For Discrete Iid Random Variables

For n independent and identically distributed discrete random variables X1, X2, …, Xn with cumulative distribution functionG and probability mass functiong the range of the Xi is the range of a sample of size n from a population with distribution function G. We can assume without loss of generality that the support of each Xi is where N is a positive integer or infinity.

The range has probability mass function

f

Read Also: Algebra Functions Examples With Answers