Boolean Algebra Laws And Theorems
Boolean Algebra is a form of mathematical algebra that is used in digital logic in digital electronics. Albebra consists of symbolic representation of a statement . Similarly, there are expressions, equations and functions in Boolean algebra as well.
The main aim of any logic design is to simplify the logic as much as possible so that the final implementation will become easy. In order to simplify the logic, the Boolean equations and expressions representing that logic must be simplified.
So, to simplify the Boolean equations and expression, there are some laws and theorems proposed. Using these laws and theorems, it becomes very easy to simplify or reduce the logical complexities of any Boolean expression or function.
The article demonstrates some of the most commonly used laws and theorem is Boolean algebra.
Outline
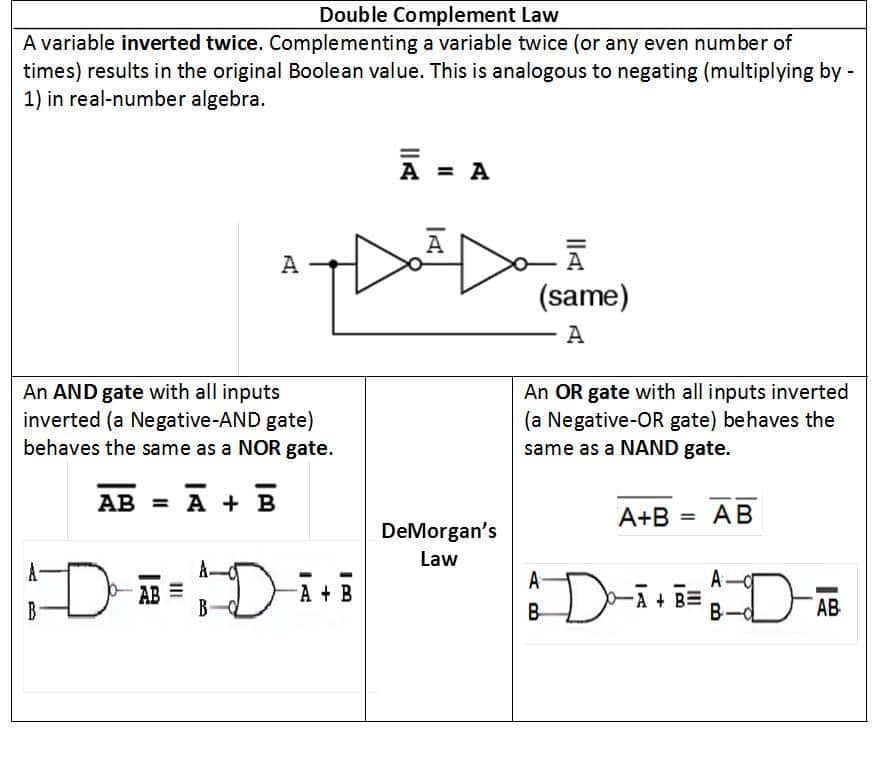
Associate Law of Addition
Statement:
Associative law of addition states that OR ing more than two variables i.e. mathematical addition operation performed on variables will return the same value irrespective of the grouping of variables in an equation.It involves in swapping of variables in groups.
The Associative law using OR operator can be written as
A+ = +C
Proof:
If A, B and C are three variables, then the grouping of 3 variables with 2 variables in each set will be of 3 types, such as , and.
According to associative law
= +C = A + = B +
We know that, A + AB = A
Now lets assume that, x = A + and y = + C
Now, find Ax = A
= AA +A
= + AC
Therefore Ax = A
State De Morgans Law: Definition
Set theory is an algorithm of set types and sets operations. For a better understanding of the multiple set operations and their inter-relationship, De Morgans laws are the best tool. De Morgans Law describes the relationship between three fundamental operations of sets: the complement of sets, the union of sets and the intersection of sets.
De Morgans Law states that the complement of the union of two sets is the intersection of their complements, and also, the complement of intersection of two sets is the union of their complements.
Depending on the inter-relation between the set-union and set-intersection, there are two types of De Morgans law that exists in set theory. They are explained below:
Boolean Algebra And Demorgans Laws
Boolean Algebra is a branch of mathematics devoted to the study of Boolean values and operators. Boolean Algebra consists of these fundamental operands and operators:
- operands : true, false
- operators: and , or , not
Note: Java has other Boolean operators, such as ^ and equivalence. This curriculum does not cover these other operators because they are not part of the AP subset.
There are many identities that have been developed to use with compound Boolean expressions. Two of the more useful identities are DeMorgan’s Laws, which are used to negate compound Boolean expressions.
-
DeMorgans Laws:
Also Check: What Are The Fields Of Geography
De Morgan’s Law Example
Let us understand De Morgan’s Law with the help of a simple example. Let the universal set U = . The two subsets are given by A = and B = .
De Morgan’s Law of Union Example: = , = . A = and B’ = . A B = . Thus, = A B
De Morgan’s Law of Intersection Example: = , ‘ = . A B = . Hence, = A B
Solved Examples On De Morgans Law
Let us look at De Morgans Law logic:
Q.1. Set \ set \ and set \ Prove that \Ans: Given: \ set \ and set \Intersection of the sets contains the common elements of both sets.\\\)\\)\Similarly, \\\)From \ \)\Hence, proved.
Q.2. If \ and set \ and \ Prove De Morgans law of intersection.Ans: We need to prove that \Given: \ and set \ and \\\\)\\)\\\\)From \,\) \
Q.3. Let \ and \ prove that \Ans: Given, \ and \\\ = \ \ = \ ..\left\)\\\\)From \ \)\.Hence, proved.
Q.4. \ and set \ and \ Prove De Morgans law of union.Ans: We need to prove that \Given: \ and set \ and \\\\)\\)\\\\)From \\) and \,\) \
Q.5. Universal set contains all possible outcomes when a dice is thrown. Set \ contains even number outcomes and set \ contains odd number outcomes. Prove that, \Ans: When a dice is thrown, the possible outcomes are \Given: \ and \\\ = \ \ = \emptyset \)\\\\)From \ :\)
Read Also: What Is Overproduction In Biology
What Are The Laws Of Boolean Algebra
The basic Laws of Boolean Algebra that relate to the Commutative Law allowing a change in position for addition and multiplication, the Associative Law allowing the removal of brackets for addition and multiplication, as well as the Distributive Law allowing the factoring of an expression, are the same as in ordinary
Negation Of A Disjunction
In the case of its application to a disjunction, consider the following claim: “it is false that either of A or B is true”, which is written as:
- ¬
- .
If either A or B were true, then the disjunction of A and B would be true, making its negation false. Presented in English, this follows the logic that “since two things are both false, it is also false that either of them is true”.
Working in the opposite direction, the second expression asserts that A is false and B is false . Knowing this, a disjunction of A and B must be false also. The negation of said disjunction must thus be true, and the result is identical to the first claim.
You May Like: What Is Grid In Geography
Theorems Of Several Variables
Theorems T6 to T12 in Table 2.3 describe how to simplify equations involving more than one Boolean variable.
Table 2.3. Boolean theorems of several variables
| Theorem | |||
|---|---|---|---|
| D = | T7 | + D = B + | Associativity |
| + = | T8 | = B + | Distributivity |
| D) + = B C + B | + D) = ( B | ||
| ) | De Morgan’s Theorem |
Commutativity and associativity, T6 and T7, work the same as in traditional algebra. By commutativity, the order of inputs for an AND or OR function does not affect the value of the output. By associativity, the specific groupings of inputs do not affect the value of the output.
The distributivity theorem, T8, is the same as in traditional algebra, but its dual, T8, is not. By T8, AND distributes over OR, and by T8, OR distributes over AND. In traditional algebra, multiplication distributes over addition but addition does not distribute over multiplication, so that × B + .
The covering, combining, and consensus theorems, T9 to T11, permit us to eliminate redundant variables. With some thought, you should be able to convince yourself that these theorems are correct.
De Morgan’s Theorem, T12, is a particularly powerful tool in digital design. The theorem explains that the complement of the product of all the terms is equal to the sum of the complement of each term. Likewise, the complement of the sum of all the terms is equal to the product of the complement of each term.
Figure 2.19. De Morgan equivalent gates
Example 1.10
Solution
Example 1.11
Example 1.12
Solution
What Are The Properties Of Boolean Algebra
Boolean algebra has three basic properties, they are:
- Commutative Property of Addition and Multiplication: Order of variables can be reversed without changing the truth of expression i.e. A + B = B + A and AB = BA
- Associative Property of Addition and Multiplication: Multiplied and added variables together with parentheses can be altered without changing the truth of expression i.e. A + = + C and A = C
- Distributive Property: Expression formed by the product of a sum when expanded and reversed shows how the terms may be factored i.e. A = AB + BC
Also Check: What Is The Electron Geometry Of Pf3
De Morgans Logic Second Law
It states that the complement of the intersection of any two sets is equal to the union of the complement of that sets.
This type of De Morgans law gives the relation of the intersection of two sets with their union of sets by using the set complement operation.
Consider any two sets A and B, the mathematical relation of De Morgans second law is given by
Union of Sets:
The union of sets and \) is the set containing all the elements in both sets \ and \ The mathematical symbol used for the union of sets is .
The union of set \ and set \ is denoted by \ mathematically. We can represent the union of two sets in the pictorial form by using Venn diagrams. The union of given sets \ and \ is represented in Venn diagrams by shading all portions of the sets \ and \ as shown below:
Example:The union of sets \ and \ given by
The union of two sets is \
It can be represented in the Venn diagram as shown below:
Negation Of A Conjunction
The application of De Morgan’s theorem to conjunction is very similar to its application to a disjunction both in form and rationale. Consider the following claim: “it is false that A and B are both true”, which is written as:
- ¬
- .
Presented in English, this follows the logic that “since it is false that two things are both true, at least one of them must be false”.
Working in the opposite direction again, the second expression asserts that at least one of “not A” and “not B” must be true, or equivalently that at least one of A and B must be false. Since at least one of them must be false, then their conjunction would likewise be false. Negating said conjunction thus results in a true expression, and this expression is identical to the first claim.
=A^\cap B^} , is proven similarly.
Also Check: How To Do Moles In Chemistry
Equivalent Gates Of Demorgans Theorem
Based on DeMorgans first and second theorems, it is observed that all the AND operators in a logical expression can be replaced with OR operators and vice versa and then inverts every term in the expression which means logic 0 to logic 1 and logic 1 to logic 0.
So, to get DeMorgans equivalent gates for AND, OR, and NOT gates, inverters are to be added for all the inputs and outputs and alter AND to OR gate and OR to AND gate.
The equivalent gates of DeMorgans laws are shown below by comparing with fundamental logical gates.
| Fundamental Logic Gates |
This section gives an example on intersection using DeMorgans law
Consider
X = and Y = and Z =
Using DeMorgans second law, we know that
C = XC YC
Here, =
= = LHS
Now, Y = and Y =
Z = and Z =
Y Z =
Y Z = = RHS
So, LHS = RHS
Proof Of De Morgans First Law

There are two proofs given for De Morgans Law, and one is a mathematical approach and the other by using Venn diagram.
De Morgans first law tells that, \
Mathematical Approach:
Let us consider \
Let \ be any element of \ then \
Therefore, \\)
Again, let \ be an arbitrary element of \ then)\
Therefore, \\) Now combine \\) and \\) we get \ i.e. \
Venn Diagram MethodConsider two sets, \ and \ the Union of sets is represented by shading the complete portion of two sets.
The Venn diagram of \\) shows all the region of Union except \ and \
We know that the complement of two sets, \ and \ are shown by shading all region of union except the given set.
The intersection of the complement of two sets shown in the below Venn diagram.
Thus, by using the Venn diagrams, we can say that, \
You May Like: What Does I Stand For In Physics
What Is De Morgan’s Law In Boolean Algebra
In Boolean algebra, De morgan’s first theorem states that when two or more variables are NOR’d together, the obtained result will be equal to the AND of the inverted variables. According to the second theorem, when two or more variables are NAND’d together it is equivalent to the OR of the inverted variables.
Generalising De Morgan Duality
In extensions of classical propositional logic, the duality still holds , since in the presence of the identities governing negation, one may always introduce an operator that is the De Morgan dual of another. This leads to an important property of logics based on classical logic, namely the existence of negation normal forms: any formula is equivalent to another formula where negations only occur applied to the non-logical atoms of the formula. The existence of negation normal forms drives many applications, for example in digital circuit design, where it is used to manipulate the types of logic gates, and in formal logic, where it is needed to find the conjunctive normal form and disjunctive normal form of a formula. Computer programmers use them to simplify or properly negate complicated logical conditions. They are also often useful in computations in elementary probability theory.
Let one define the dual of any propositional operator P depending on elementary propositions p, q, … to be the operator P
Read Also: Is Living Environment The Same As Biology
De Morgan’s Law Truth Table
In boolean algebra, we make use of logic gates. These logic gates work on logic operations. Here, A and B become input binary variables. “0’s” and “1’s” are used to represent digital input and output conditions. Thus, using these conditions we can create truth tables to define operations such as AND , OR , and NOT . By using logic operations as well as truth tables, we can state and prove De Morgan’s laws as follows:
First De Morgan’s Law states that when two or more input variables are ORed and then negated, the result is equal to the AND of the complements of the individual input variables. \ = \\. To prove this theorem we can use the truth table as given below:
| INPUTS |
Generalized Formulas for infinite unions and intersections,
- \^ = \bigcap_^ A_^\)
- \^ = \bigcup_^ A_^\)
In Boolean Algebra,
De Morgan’s Law Statement
Demorgan’s law can be used in boolean algebra as well as in set theory to simplify mathematical expressions. Suppose we have two sets A and B that are subsets of the universal set U. A’ is the complement of A and B’ is the complement of set B. ” is the symbol for intersection and ” is used to denote the union. Then the De Morgan’s laws are given below.
De Morgan’s Law of Union: The complement of the union of the two sets A and B will be equal to the intersection of A’ and B’ . This is also known as De Morgan’s Law of Union. It can be represented as = A B. We can also generalize this law. Suppose we have n sets given by , A_, …, A_\)} then formula is given by \^ = \bigcap_^ A_^\).
De Morgan’s Law of Intersection: The complement of the intersection of A and B will be equal to the union of A’ and B’. This condition is called De Morgan’s law of Intersection. It can be given by = A B. Similarly, as above this law can be generalized by the formula \^ = \bigcup_^ A_^\).
Also Check: Glencoe Algebra 2 Chapter 5 Answer Key
Application Of Boolean Algebra Laws
Boolean algebra is employed to simplify logic circuits. Simplification often leads to having fewer components. Moreover, many cases can be found where two logic circuits lead to the same results. The two circuits, in this case, are equivalent to each other. Boolean algebra can help to verify and identify these circuits. This helps to reduce the number of gates in a circuit or synthesize a logic gate by some other gates, when necessary.
Figure 1 Showing the first and second De Morgan law equivalent circuits. Another way to show inputs to AND and OR gates if complements of signals A and B are the entries.
De Morgans Law: Theorem Proofs Examples
De Morgans Law is a collection of boolean algebra transformation rules that are used to connect the intersection and union of sets using complements. De Morgans Law states that two conditions must be met. These conditions are typically used to simplify complex expressions. This makes performing calculations and solving complicated boolean expressions easier.
According to De Morgans Law logic, the complement of the union of two sets is equal to the intersection of their separate complements. Furthermore, the complement of two sets intersecting is equal to the sum of their separate complements. Venn diagrams make it simple to visualise these laws. We will study Demorgans Laws statements, how to prove them, how to apply them, and De Morgans law example in this article.
Recommended Reading: Riemannian Geometry Do Carmo Solutions
De Morgan’s Law Proof
In set theory, Demorgan’s Law proves that the intersection and union of sets get interchanged under complementation. We can prove De Morgan’s law both mathematically and by taking the help of truth tables.
The first De Morgan’s theorem or Law of Union can be proved as follows:
Let R = ‘ and S = A’ B’. Suppose we choose an element y that belongs to R. This is denoted as y R.
y ‘
y A and y B
y A’ and y B’
y A’ B’
y S
Thus, we conclude that R S …
Now suppose we have an arbitrary element z that belongs to set S. Then z S
z A’ B’
z A’ and z B’
z A and z B
z
z R
Hence, S R …
From and we infer that S = R or = A B. Thus, this theorem is proved.
The second De Morgan’s theorem or law of Intersection can be mathematically proved using the following steps:
Let G = ‘ and H = A’ U B’
Let an element y belong to G. y G.
y ‘
y A or y B
y A’ or y B’
y A’ U B’
This implies that G H …
If z is an arbitrary element of H then z H
z A’ U B’
z A’ or z B’
z A or z B
z
z H
Therefore, H G …
Now when we combine and we can say that G = H or = A B. Hence, we have successfully proved the second theorem.