What Is Standard Algorithm In Math

The Standard Multiplication Algorithmwith A Two

I explain how to multiply by a two-digit number . This involves two separate multiplications and lastly adding their results. In the second multiplication, one has to add a zero in the ones place. This is because we’re actually multiplying by a multiple of ten .

In this second part, we take a look at a word problem that gives info for the wages of two persons and asks who earns more in a week, and how much more. We need to use 2-digit multiplication to solve it.

Multiplication With Regrouping: Standard Algorithm

Multiplying two-digit numbers can be intimidating, especially if the numbers are large. All that regrouping can be confusing. Which number goes where? And better yet, why?

Help students master multiplication with regrouping using the two latest books from KUCRL: Multiplication With Regrouping: Partial Products and Multiplication with Regrouping: Standard Algorithm.

Based on the concrete representational abstract teaching sequence from the Strategic Math Series, this manual applies the same procedures to multiplication with regrouping. The Standard Algorithm book shows students the shortened way to multiply and regroup. Students not only master multiplication, but come to understand exactly what they are doing and why.

Researched and written by Margaret Flores and Bradley Kaffar, the manual is available either as an electronic PDF or a spiral-bound printed copy shop.kucrl.ku.edu . Both formats contain progress charts, place value mats, student learning sheets, and ideas for dice games to promote maintenance Dice and blocks not included.

• An Introduction to Multiplication with Regrouping: Standard Algorighm, including Students Who Need This Manual, Results of Field Tests, Prerequisite Skills, and the Instructional Sequence

The Standard Multiplication Algorithm

This is a complete lesson with explanations and exercises about the standard algorithm of multiplication , meant for fourth grade. First, the lesson explains how to multiply a two-digit number by a single-digit number, then has exercises on that. Next, the lesson shows how to multiply how to multiply a three or four-digit number, and has lots of exercises on that. there are also many word problems to solve.

The standard algorithm of multiplication is based on the principle that you already know: multiplying in parts : simply multiply ones and tens separately, and add.

However, in the standard way the adding is done at the same time as multiplying. The calculation looks more compact and takes less space than the easy way to multiply you have learned.

The standard way to multiply “The easy way”

Also Check: My.hrw.com Answer

Examples Of Alternative Algorithms

Partial-Sums Algorithm

                       2 6 8                     + 4 8 3                     _______                       6 0 01. Add 100s            1 4 02. Add 10s               1 13. Add 1s            _______4. Add partial sums    7 5 1

Partial Product Algorithm

          67        x 53     _______50 x 60 300050 x 7   3503 x 60   1803 x 7     21     _______        3551

Why Not Just Teach The Traditional Us Algorithm Here’s Why:

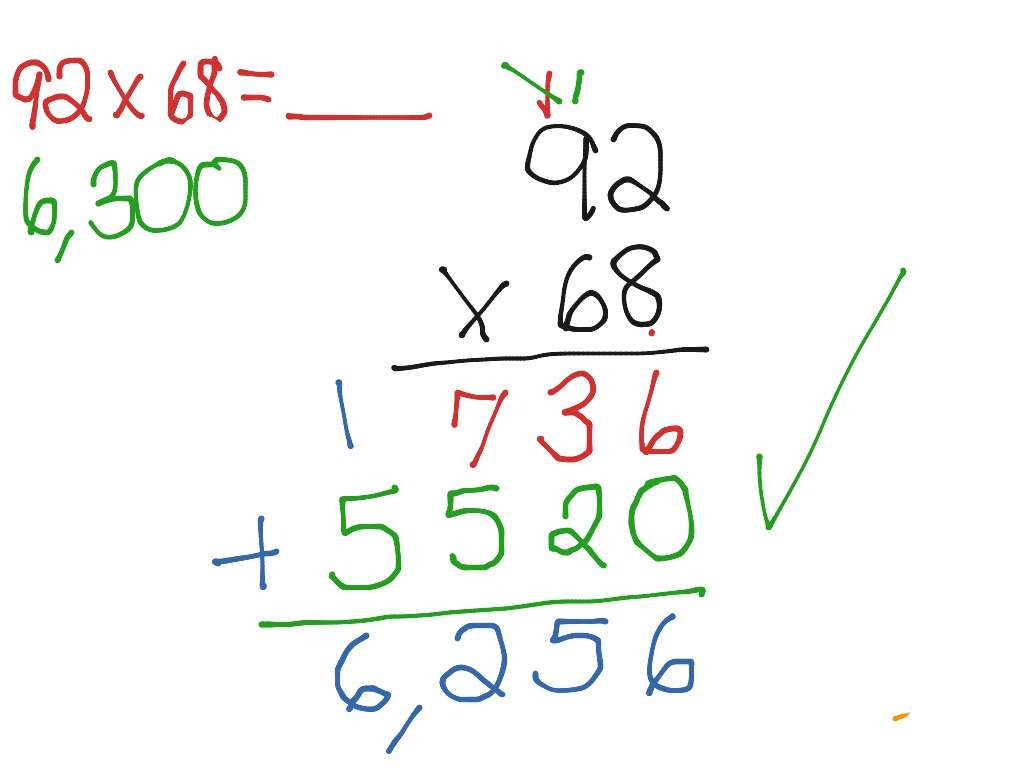
Below is a piece written by our very own Debra Rawlins, Lower School Math Coordinator.Kamii et al. found that rote learning of traditional algorithms can actually interfere with a childs development of number sense. All that said, we do value and teach the U.S. traditional algorithm. Prior to learning the algorithm, students engage in developing their own strategies for multi-digit computation, creating algorithms that make sense to them. They can look at a problem as a whole, analyze the relationships of the numbers, and decide on an approach. Through this process, they expand their knowledge of place value, and how the operations of addition andsubtraction behave, or specifically, their underlying properties. They also see themselves as unique learners who can solve problems flexibly using a variety of strategies.After students have had extensive experience developing and sharing their own strategies, they examine the traditional algorithm. By this time, they have attained powerful number sense and they enjoy the challenge of taking apart the U.S. algorithm to understand why it works. Thomas P. Carpenters

Recommended Reading: Beth Thomas Brother Jonathan

What Is The Standard Algorithm

Before learning the standard algorithm in Math, let us understand the concept of the standard algorithm. Everything we do in our daily life is linked to the standard algorithm. From waking up in the morning to sleeping at night, we have been following an algorithm like everyone else on this planet. For instance, if we need to bake a fluffy and delicious cake, we must follow certain steps, or the result will be garbage. There are step-by-step procedures to bake a cake and get a perfect cake out of the oven are as follows:

Step 1: Find the recipe for the cake you want to bake.

Step 2: Look for all the ingredients, and if you cant find them go to the store to buy them.

Step 3: Mix all the ingredients in the proper order by taking the correct measure of each ingredient as instructed in the recipe.

Step 4: Put the mixture in a pan and bake for a set time.

Step 5: When baked, take it out of the oven and refrigerate it for frosting.

Step 6: Take it out of the refrigerator and decorate it according to your desire.

Thats it you have now learned how to make a delicious cake all by yourself. If you keep using these steps in the future, you wont have to look at the recipe. You will become a master of tasty baking cakes. Although baking a cake is not an algorithm, this was necessary to understand why a step-by-step approach is essential.

What Is An Algorithm Algorithm Basics

The word Algorithm means A set of rules to be followed in calculations or other problem-solving operations Or A procedure for solving a mathematical problem in a finite number of steps that frequently by recursive operations .

Therefore Algorithm refers to a sequence of finite steps to solve a particular problem.

Algorithms can be simple and complex depending on what you want to achieve.

It can be understood by taking the example of cooking a new recipe. To cook a new recipe, one reads the instructions and steps and executes them one by one, in the given sequence. The result thus obtained is the new dish cooked perfectly. Every time you use your phone, computer, laptop, or calculator you are using Algorithms. Similarly, algorithms help to do a task in programming to get the expected output.

The Algorithm designed are language-independent, i.e. they are just plain instructions that can be implemented in any language, and yet the output will be the same, as expected.

Read Also: Half Life Formulas Chemistry

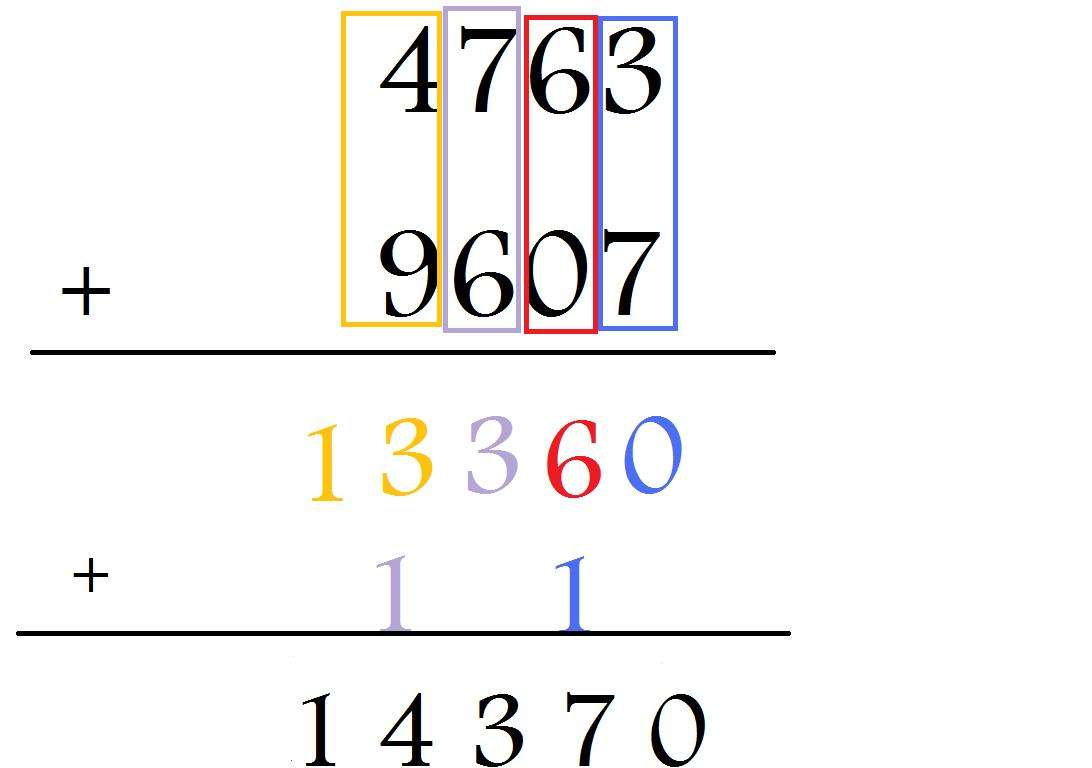
What Is Standard Algorithm Addition

The standard algorithm for addition has three simple rules: Rule 1: Line up the numbers vertically by matching the place values and start with the ones place. Rule 2: Add together the numbers that share the same place value again start with the ones place. Rule 3: Regroup if necessary.Oct 12 2017

Standard Algorithm Vs Invented Strategies

• Differentiation, Math, Planning

When Common Core came on the scene long ago there were many complaints regarding the invented strategies that teachers are to teach students in math. I heard over and over, Why dont you just teach them the old fashioned way ? I imagine you have heard that too. I found myself at a loss trying to explain to parents why exactly it was suddenly different though, I dont think it was. I remember hearing in teacher college that everyday math incorporated something similar, trying to get students to think deeper about the math strategies. Nonetheless, it got me thinking: how can I understand and explain this better?

You May Like: Simplify Imaginary Numbers Worksheet

Manipulation Of Symbols As Place Holders For Numbers: Algebra

Muhammad ibn Ms al-Khwrizm, a Persian mathematician, wrote the Al-jabr in the 9th century. The terms “algorism” and “algorithm” are derived from the name al-Khwrizm, while the term “algebra” is derived from the book Al-jabr. In Europe, the word “algorithm” was originally used to refer to the sets of rules and techniques used by Al-Khwarizmi to solve algebraic equations, before later being generalized to refer to any set of rules or techniques. This eventually culminated in Leibniz‘s notion of the calculus ratiocinator :

A good century and a half ahead of his time, Leibniz proposed an algebra of logic, an algebra that would specify the rules for manipulating logical concepts in the manner that ordinary algebra specifies the rules for manipulating numbers.

What Are The Alternative Algorithms Why Are These Part Of The Everyday Mathematics Curriculum

For decades, all American schoolchildren have been taught one standard procedure for each of the four basic operations of arithmetic. These “standard” algorithms, like the regrouping algorithm for multi-digit subtraction and the long division algorithm, are not the only ways to perform these operations. There are many alternative algorithms taught in other countries. Compared to the standard U.S. algorithms, many of these alternative algorithms are more efficient and easier to learn.

Research has shown that teaching the standard U.S. algorithms fails with large numbers of children, and that alternative algorithms are often easier for children to understand and learn. For this reason, Everyday Mathematics introduces children to a variety of alternative procedures in addition to the customary algorithms. Examples of a couple alternative algorithms are below:

Also Check: What Is The Difference Between Electron Geometry And Molecular Geometry

Alternate Algorithms For Subtraction

Universal, student invented algorithms:

One strategy that you often see when children are inventing ways to subtract is called the “negative numbers” algorithm. In this algorithm, you subtract as much as you can in each place value, using negative numbers to represent the amount left to be subtracted when the digit in the subtrahend is greater than the digit in the minuend. There are, of course, varying ways of representing this algorithm:

Another common strategy that is significantly different from the standard algorithm is to subtract in each place value, going left to right. This is often represented as a set of subtraction problems as one might do if one were trying to solve the problem using a mental math strategy. This can also be represented as a subtraction in columns by crossing out digits where necessary, and it can include the same sorts of trading steps as the standard algorithm, though the order is quite different..

Mental math version:

Friendly numbers strategies :

Alternate algorithms for teaching:

For example–if you look at the first of these examples carefully, you’ll see that the trade of 1 thousand for 10 hundreds was made before the trade of 1 hundred for 10 tens, which was made before the trade of 1 ten for 10 ones.

Jb Rosser And Sc Kleene

J. Barkley Rosser defined an ‘effective method’ in the following manner :

“‘Effective method’ is used here in the rather special sense of a method each step of which is precisely determined and which is certain to produce the answer in a finite number of steps. With this special meaning, three different precise definitions have been given to date. . The simplest of these to state says essentially that an effective method of solving certain sets of problems exists if one can build a machine which will then solve any problem of the set with no human intervention beyond inserting the question and reading the answer. All three definitions are equivalent, so it doesn’t matter which one is used. Moreover, the fact that all three are equivalent is a very strong argument for the correctness of any one.”

Rosser’s footnote No. 5 references the work of Church and Kleene and their definition of -definability, in particular, Church’s use of it in his An Unsolvable Problem of Elementary Number Theory Herbrand and Gödel and their use of recursion, in particular, Gödel’s use in his famous paper On Formally Undecidable Propositions of Principia Mathematica and Related Systems I and Post and Turing in their mechanism-models of computation.

Stephen C. Kleene defined as his now-famous “Thesis I” known as the ChurchTuring thesis. But he did this in the following context :

Don’t Miss: Geometry Dash Hack Steam

Emil Post And Alan Turing

Emil Post described the actions of a “computer” as follows:

“…two concepts are involved: that of a symbol space in which the work leading from problem to answer is to be carried out, and a fixed unalterable set of directions.

His symbol space would be

“a two-way infinite sequence of spaces or boxes… The problem solver or worker is to move and work in this symbol space, being capable of being in, and operating in but one box at a time…. a box is to admit of but two possible conditions, i.e., being empty or unmarked, and having a single mark in it, say a vertical stroke.

“One box is to be singled out and called the starting point. …a specific problem is to be given in symbolic form by a finite number of boxes being marked with a stroke. Likewise, the answer is to be given in symbolic form by such a configuration of marked boxes…

“A set of directions applicable to a general problem sets up a deterministic process when applied to each specific problem. This process terminates only when it comes to the direction of type “. See more at PostTuring machine

Turinghis model of computation is now called a Turing machinebegins, as did Post, with an analysis of a human computer that he whittles down to a simple set of basic motions and “states of mind”. But he continues a step further and creates a machine as a model of computation of numbers.

Turing’s reduction yields the following:

“We may now construct a machine to do the work of this computer.”

Why Learn Alternate Algorithms

The traditional algorithm that we learned in school has some great advantages–it’s compact it shows all of the important steps it’s thoroughly de-bugged and it’s what most people use .

The traditional algorithm, however, doesn’t always fit the way that children think. Using manipulatives to work through the steps helps make the standard algorithm make sense to children, but there are other approaches that have other advantages too. If you teach addition and subtraction through asking good problems and asking children to solve the problems in ways that make sense to them, children will come up with a range of strategies and ways of recording those strategies. Spending time developing childrens ideas is often time well spent in terms of children getting a robust understanding of how addition and subtraction works and what it represents. If you teach by questioning and problem solving you’ll see a lot of different ideas and strategies that children come up with.

The other situation where learning other algorithms can be useful as a teacher is that there are some alternate ways of adding and subtraction that are sometimes used as a teaching strategy for children who aren’t ready for the standard algorithms.

Also Check: What Does Standardization Mean In Chemistry

The Importance Of Math Manipulatives

Math manipulatives are an important part of building conceptual understanding. Manipulatives arent always purchased. It is something concrete that you provide the student with that can be changed so that students can grasp an abstract concept.

One of my colleagues used to always say that the brain thinks in pictures. This is very true especially when introducing a new concept or trying to clear up misconceptions. Students MUST have an anchor to refer back to when learning new concepts. Normally in math if the concept is introduced in the previous grade level that instruction will serve as the anchor. If the concept is brand new, then the teacher has to create the anchor with manipulatives.

Where theres no anchor, students will try to visualize a math concept that doesnt have a frame of reference.

What Is An Algorithm

Karen Fuson and Sybilla Beckmann, in their Standard Algorithms in the Common Core State Standards cite a CCSSM Progression document.

In mathematics, an algorithm is defined by its steps, and not by the way those steps are recorded in writing.

Hyman Bass, in his article from Teaching Children Mathematics, Computational Fluency, Algorithms, and Mathematical Proficiency: One Mathematicians Perspective agrees.

An algorithm consists of a precisely specified sequence of steps that will lead to a complete solution for a certain class of computational problems.

So far, so good. We have accord on the meaning of algorithm.

Recommended Reading: Algebra And Trigonometry 3rd Edition Stewart Redlin Watson Pdf

Math Intervention Instructional Strategies

When it comes to intervention strategies, the students grade level doesnt really matter . The students deficit will determine which intervention instructional strategy. For example, if a student in ninth and fifth grade are struggling with mixed numbers the intervention strategies will be the same, because the deficit is the same.

When I see Facebook posts where teachers are asking for math intervention instructional strategies before school has started, I am always confused because the deficit hasnt been identified yet.

Oftentimes in math intervention teachers try to move students too quickly to the algorithm because thats whats being tested. If a student is still building conceptual understanding of a concept and isnt ready for the algorithm and you introduce the algorithm anyway, youre basically setting yourself up for failure.

Students have to be given time to build their conceptual understanding and then transition to the algorithm. The algorithm is the abstract understanding of the conceptual. For instance, the student in the photo above was able to convert a fraction greater than a whole to a mixed number using fraction wheels ONLY. By the end of the year, she had weaned herself from the conceptual to the algorithm because I practiced the conceptual along with the algorithm. By doing this it created a natural progression/ transition from the conceptual to the algorithm.