Global Maximum And Minimum
The maximum or minimum over the entire function is called an “Absolute” or “Global” maximum or minimum.
There is only one global maximum but there can be more than one local maximum or minimum.
Assuming this function continues downwards to left or right:
- The Global Maximum is about 3.7
- The Global Minimum is Infinity
Definition Of Minimum Value
The following texts are the property of their respective authors and we thank them for giving us the opportunity to share for free to students, teachers and users of the Web their texts will used only for illustrative educational and scientific purposes only.
All the information in our site are for educational uses.
The information of medicine and health contained in the site are of a general nature and purpose which is purely informative and for this reason may not replace in any case, the council of a doctor or a qualified entity legally to the profession.
http://esu4vocabularystrategies.wikispaces.com
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship please send us an e-mail and we will remove your text quickly.
Fair use is a limitation and exception to the exclusive right granted by copyright law to the author of a creative work. In United States copyright law, fair use is a doctrine that permits limited use of copyrighted material without acquiring permission from the rights holders. Examples of fair use include commentary, search engines, criticism, news reporting, research, teaching, library archiving and scholarship. It provides for the legal, unlicensed citation or incorporation of copyrighted material in another author’s work under a four-factor balancing test.
Google key word : minimum value
How Do You Solve Maximum And Minimum
Finding Maxima & Minima
Read Also: Geopolitics Definition Ap Human Geography
Do All Functions Have A Minimum And A Maximum
A function does not necessarily have a minimum or maximum. For example, the function f = x does not have a minimum, nor does it have a maximum. This can be seen easily as follows. Suppose the function has a minimum at x = y. Then fill in y-1 and the function has a smaller value. Therefore we have a contradiction and y was not the minimum, and hence the minimum does not exist. An equivalent proof can be given for the maximum.
The function f = x2 does have a minimum, namely at x = 0. This is easily verified since f can never become negative, since it is a square. At x = 0, the function has value 0, so this must be the minimum. It does not have a maximum, which can be proven using the exact same argument as we used before.
What Is Minimum In Math
Minimum in mathematics, the lowest function value compared to its values in all fairly close points. In mathematical analysis, the minimum is one of the types of extreme, the lowest function value at a given interval. Satisfying the minimum condition is n-ar operation , returning the smallest of the numbers.
The Online Median calculator allows everybody to easily calculate the median value of any set of numbers in 3 simple steps. Calculate Median, Mean, Mode, Range, Frequency values, no matter whether you have a set of whole numbers or fractions. Median formula is still the same. Though the calculus is simple and can be made even in excel, for big set of symbols you may need more convenient tool.
Read Also: 8th Grade Algebra Word Problems
Limitations Of The Maximum And Minimum
The maximum and minimum are very sensitive to outliers. This is for the simple reason that if any value is added to a data set that is less than the minimum, then the minimum changes and it is this new value. In a similar way, if any value that exceeds the maximum is included in a data set, then the maximum will change.
For example, suppose that the value of 100 is added to the data set that we examined above. This would affect the maximum, and it would change from 41 to 100.
Many times the maximum or minimum are outliers of our data set. To determine if they indeed are outliers, we can use the interquartile range rule.
How Do You Find The Relative Maximum On A Ti 83
Also How do you find the absolute max and min on a graphing calculator?
What is maximum and minimum value of a function?
The function has a minimum value at x = a if f = 0. and f = a positive number. The function has a maximum value at x = a if f = 0. and f = a negative number. In the case of the maximum, the slope of the tangent is decreasing it is going from positive to negative.
How do you find the maximum value of a sine function? The maximum value of the function is M = A + |B|. This maximum value occurs whenever sin x = 1 or cos x = 1. The minimum value of the function is m = A |B|.
Don’t Miss: What Happened To Beth Thomas Brother
How Do You Find The Maximum Of A Set Of Data
The maximum and minimum also make an appearance alongside the first, second, and third quartiles in the composition of values comprising the five number summary for a data set. The minimum is the first number listed as it is the lowest, and the maximum is the last number listed because it is the highest.
Where can I find xmax and xmin?
xmin and xmax are the leftmost and rightmost values to use on the xaxis. If we enter xmin=5 and xmax=3, we are saying to use xvalues between x = 5 and x = 3 inclusive for the graph, indicated on paper by using a closed interval . xscl refers to the units to use on the xaxis.
How do you find the xmin and xmax of a function?
How do you do fMin on a TI 84? From the main screen press and select 6:fMin(. Press . Press . Press and to display the results.
What Is Max In Math
The graph is a parabola. The function will have a minimum if the leading coefficient is positive and a maximum if the leading coefficient is negative. The function is written in vertex form the vertex is at and represents the maximum or minimum. If a> 0 there is a minimum, and if a< 0 there is a maximum.
You May Like: Cpm Algebra 2 Chapter 1 Answers
How Do You Find The Relative Maximum On A Graphing Calculator
What is the maximum feature on a graphing calculator? Graph the function in a viewing window that contains the minimum and/or maximum values of the function. Press to access the Calculate menu. Press to find the minimum, or press to find the maximum.
How do you find the maximum and minimum value?
To find the maximum or minimum value of a quadratic function, start with the general form of the function and combine any similar terms. For example, if youre starting with the function f = 3x + 2x x^2 + 3x^2 + 4, you would combine the x^2 and x terms to simplify and end up with f = 2x^2 + 5x + 4.
How do you find the max value of a function in Python? Python max
Is There A Between Maximum And Minimum
To find the maximum or minimum value of a quadratic function, start with the general form of the function and combine any similar terms. For example, if youre starting with the function f = 3x + 2x x^2 + 3x^2 + 4, you would combine the x^2 and x terms to simplify and end up with f = 2x^2 + 5x + 4.
Recommended Reading: Geometry Basics Homework 2 Segment Addition Postulate
Find The Minimum And Maximum Value Of $f=
Let $a, b, c \in \Bbb R$ satisfy $a^2+b^2+c^2=21$. Find the minimum and maximum value of $$F=|a-2b|+|b-2c|+|c-2a|$$
I found $7\le F \le \sqrt$ but couldn’t prove it. I was thinking of the following inequality:
$$|x_1+x_2+\cdots+x_n|\le|x_1|+|x_2|+\cdots+|x_n|\le \sqrt$$
but they are not really efficient. Does anyone know how to solve this problem or know where it first appeared?
- trungbk7 hours ago
- $\begingroup$Could it be done using Lagrange multipliers when assuming $a> 2b$ and $b> 2c$ and all the permutations, and then accounting for symmetry?$\endgroup$
The min and max bounds of $7$ and $\sqrt$ are indeed correct. Let $$F_L = |a + b + c|$$ and $$F_U = \sqrt$$By the inequality you’ve proposed, we have $F_L \le F \le F_U$, and presumably you’ve performed the steps to show that $\min_ F_L = 7$ and $\max_F_U = \sqrt$ the values to obtain the min and max for these lower and upper bounds are $ = $ and $ = $. Substituting these in for $F$ also obtains the lower and upper bounds.
How Do You Find The Max And Min On A Ti 83 Plus

How do you find the maximum of a graph? To find the maximum, we must find where the graph shifts from increasing to decreasing. To find out the rate at which the graph shifts from increasing to decreasing, we look at the second derivative and see when the value changes from positive to negative.
How do you find the max value on a TI 89? TI-89 / TI-92
You May Like: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate Answers
Local Extrema And Critical Points
Consider the function \ shown in Figure \. The graph can be described as two mountains with a valley in the middle. The absolute maximum value of the function occurs at the higher peak, at \. However, \ is also a point of interest. Although \\) is not the largest value of \, the value \\) is larger than \\) for all \ near 0. We say \ has a local maximum at \. Similarly, the function \ does not have an absolute minimum, but it does have a local minimum at \ because \\) is less than \\) for \ near 1.
Definition: Local Extrema
A function \ has a local maximum at \ if there exists an open interval \ containing \ such that \ is contained in the domain of \ and \f\) for all \. A function \ has a local minimum at \ if there exists an open interval \ containing \ such that \ is contained in the domain of \ and \f\) for all \. A function \ has a local extremum at \ if \ has a local maximum at \ or \ has a local minimum at \.
Note that if \ has an absolute extremum at \ and \ is defined over an interval containing \, then \\) is also considered a local extremum. If an absolute extremum for a function \ occurs at an endpoint, we do not consider that to be a local extremum, but instead refer to that as an endpoint extremum.
Definition: Critical Points
Let \ be an interior point in the domain of \. We say that \ is a critical point of \ if \=0\) or \\) is undefined.
Theorem \: Fermats Theorem
If \ has a local extremum at \ and \ is differentiable at \, then \=0.\)
Proof
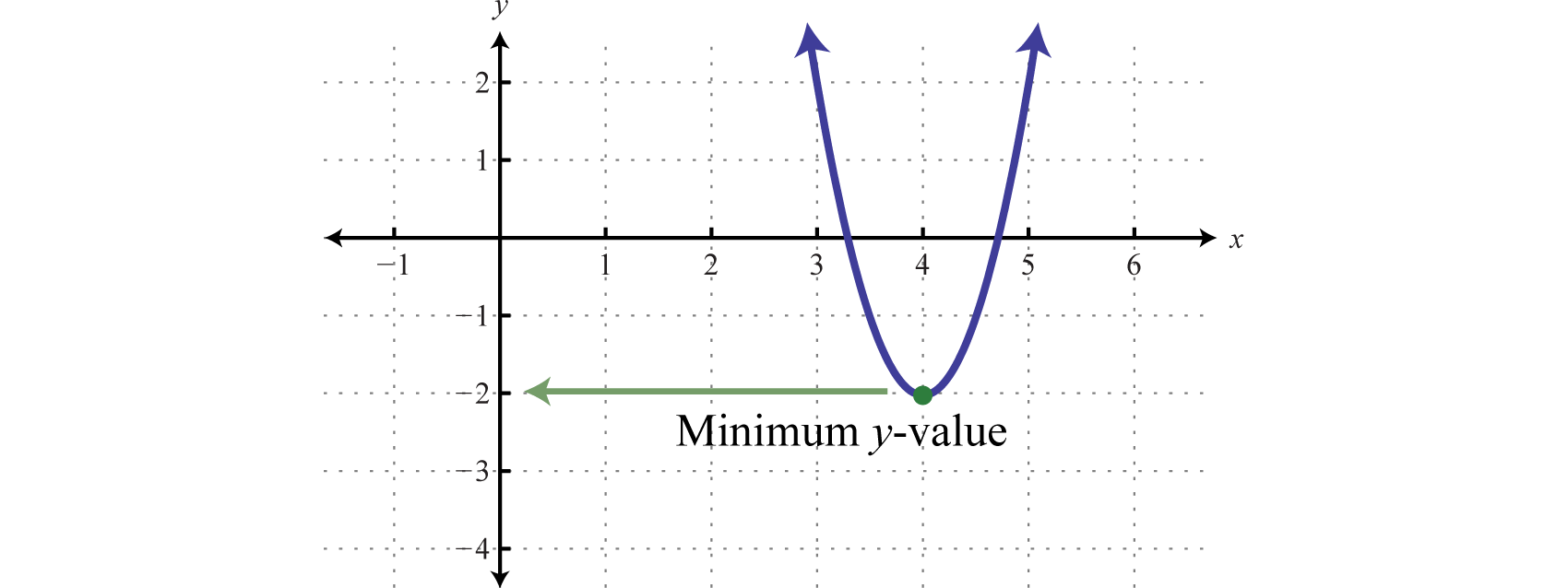
How Do You Find The Minimum Value Of A Graph
If your quadratic equation has a positive a term, it will also have a minimum value. You can find this minimum value by graphing the function or by using one of the two equations. If you have the equation in the form of y = ax^2 + bx + c, then you can find the minimum value using the equation min = c b^2/4a.
Read Also: Abiotic Science Definition
The Turning Points Of A Graph
WE SAY THAT A FUNCTIONf has a relative maximum value at x = a, if f is greater than any value immediately preceding or follwing.
We call it a “relative” maximum because other values of the function may in fact be greater.
We say that a function f has a relative minimum value at x = b, if f is less than any value immediately preceding or follwing.
Again, other values of the function may in fact be less. With that understanding, then, we will drop the term relative.
The value of the function, the value of y, at either a maximum or a minimum is called an extreme value.
Now, what characterizes the graph at an extreme value?
The tangent to the curve is horizontal. We see this at the points A and B. The slope of each tangent line — the derivative when evaluated at a or b — is 0.
f ‘ = 0.
Moreover, at points immediately to the left of a maximum — at a point C — the slope of the tangent is positive: f ‘ > 0. While at points immediately to the right — at a point D — the slope is negative: f ‘ < 0.
In other words, at a maximum, f ‘ changes sign from + to .
At a minimum, f ‘ changes sign from to + . We can see that at the points E and F.
We can also observe that at a maximum, at A, the graph is concave downward. While at a minimum, at B, it is concave upward.
A value of x at which the function has either a maximum or a minimum is called a critical value. In the figure —
— the critical values are x = a and x = b.
Example 1. Let f = x2 6x + 5.
f
Local And Absolute Minima
A local minimum, also referred to as a relative minimum, is a point a within a given interval of a function that satisfies the condition of being the smallest value within the given interval. Using typical function notation:
f f for all x in the given interval
In contrast, an absolute minimum, also referred to as a global minimum, is the smallest value of f across its entire domain:
f f for all x
The figure above shows a local and an absolute minimum for f. Note that while the figure only shows two minima, a function can have any number of minima, not just two.
Don’t Miss: Core Connections Algebra Chapter 4
Math: How To Find The Minimum And Maximum Of A Function
Finding the minimum or maximum of a function can be very useful. It often comes up in optimization problems that do not have constraints, or in which the constraints do not prevent the function from reaching its minimum or maximum.
These types of problems occur a lot in practice. An example would be determining the price of a certain article. If you know the demand for a given price , you can calculate the price for which you will make the most profit. This can be formulated as finding the maximum of the profit function.
The minimum and maximum of a function are also called extreme points or extreme values of the function. They can be local or global.
Maximum And Minimum Facts For Kids
In mathematics, the maximum and minimum of a set A is the largest and smallest element of A. They are written as and , respectively. Similarly, the maximum and minimum of a function are the largest and smallest value that the function takes at a given point. Together, they are known as the extrema .
Minimum means the least you can do of something. For example, if the minimum amount of dollars you must pay for something is seven, then you cannot pay six dollars or less . You can do more than the minimum, but no less. Maximum means the most you can have of something. For example, if the maximum amount of oranges you can juggle is five, you cannot juggle more than five oranges. You can do the maximum or less.
Also Check: Michael Jackson’s Biological Children
How Do You Find The Minimum And Maximum Values Of A Function
Solution:
A function means a correspondence from one value x of the first set to another value y of the second set. The highest value of a function is considered the maximum value of the function, and the lowest value of the function is considered the minimum value of the function.
There are some techniques for determining a function’s maximum or minimum value.
- Find the derivative of the function and equip it to zero.
- Find the roots of the differentiated equation.
- Double differentiate the original function and replace the root values in the second differentiated expression.
- If the value turns out to be negative, the particular root value Maximum occurs. Then replace the value in the original expression to get the maximum of the function.
- If the value of the double derivative after root substitution is positive, the minimum occurs. Then replace the value of the original equation to get the minimum value of the function.
- If the second derivative is zero: then find the highest derivatives of the function and replace the value of the root in the expression for the nth order derivative. If it is positive, it will give the maximum function to the particular root.
Example: y = x3 – 3×2 + 5
y = x3 – 3×2 + 5 ————-
Differentiate both of side , w.r.t – x.
dy/dx = d/dx – d/dx + d/dx
3×2 – 6x + 0