Calculate The Absolute Deviations
Next, we will find the absolute deviation of each individual value from the mean.
To do so, highlight the top of column L2 and type in the following formula:
=abs)
Heres how to actually type in this formula:
- Press 2nd, then press 0. Then press abs(. This will input abs( in the formula.
- Press 2nd, then press 1. Now you will have abs(L1 in the formula.
- Press the minus button. Now you will have abs(L1- in the formula.
- Press 2nd, then press STAT. Scroll over to MATH and then press 3. Now you will have abs(L1-mean( in the formula.
- Press 2nd, then press 1. Now you will have abs(L1-mean(L1 in the formula.
- Press ) twice. Now you will have abs), which is the final formula.
Once you press Enter, the absolute deviations will appear in column L2:
Relation To Standard Deviation
The MAD may be used similarly to how one would use the deviation for the average.In order to use the MAD as a consistent estimator for the estimation of the standard deviation
- =\sigma }\operatorname ^\approx 0.67449\sigma .}
This form is used in, e.g., the probable error.
In the case of complex values , the relation of MAD to the standard deviation is unchanged for normally distributed data.
Some Easy Mad Examples
Lets look at two quick examples. Below are two sets of data. What is the mean absolute deviation in each case?
| Data Set A | |
| 3, 3, 7 ,7 | 1, 2, 7, 10 |
Before we calculate MAD, notice that the mean, or average, of both data sets is 5. In Data Set A, however, the data is more closely clustered around the mean. This tells us that MAD must be smaller for Data Set A than it is for Data Set B since the distances between the data values and the mean are smaller. We can see this more clearly by plotting our data onto dot plots.
Using these dot plots, we can visualize the deviations.
For Data Set A, we see that every single data point deviates from the mean by 2. Calculating MAD in this case is easy the average of four twos is just two!
Concretely, what do these figures tell us? In the first instance, MAD tells us that, on average, the values in Data Set A deviate from the mean by 2.
In the second case, MAD tells us that, on average, the values in Data Set B deviate from the mean by 3.5.
You May Like: What Is Succession In Biology
How Mad Calculator Works:
The calculation becomes very easy with this online Mean Absolute Deviation Calculator. Just stick to the following points:
Inputs:
- First of all, choose from the dropdown menu around which the data is dispersed.
- Very next, enter the numbers in the designated field.
- Lastly, hit the calculate button.
Note:
If you select the other from the dropdown menu, then enter the value around which the data is distributed.
Outputs:
Once you enter in all the fields, the Mad calculator shows:
- Mean Absolute Deviation of data set.
- Step-by-Step Calculation.
Why Do The Standard Forecast Error Calculations Make Forecast Improvement So Complicated And Difficult

It is important to understand forecasting error, but the problem is that the standard forecast error calculation methods do not provide this good understanding. In part, they don’t let tell companies that forecast how to make improvements. If the standard forecast measurement calculations did, it would be far more straightforward and companies would have a far easier time performing forecast error measurement calculation.
You May Like: How To Learn Psychology Fast
How The Mad Performs For Different Distributions
The following image shows histograms for 10,000 random numbers drawn from four different distributions: a normal distribution, double exponential distribution, Cauchy distribution and Tukey-Lambda distribution.
- Normal: the MAD is slightly less than the standard deviation as it downw-eights the tails. This is one reason not to use the MAD for normal distributions.
- Double exponential: The SD is usually too large while the MAD is about the same as it would be for the normal.
- Cauchy: the SD is very large, while the MAD is on y just a little larger than normal.
- Tukey-Lambda Distribution: this distribution has truncated tails the SD and MAD are about the same.
What Is Mean Absolute Deviation Formula
There are two formulas to find the mean absolute deviation. One is for the ungrouped data and another is for the grouped data. Let x1, x2, …. xn be the data set and let be its mean of the ungrouped data. And, f is the frequency of the data point xi, for the grouped data. The mean absolute deviation formulas for the two types of data are as follows.
Recommended Reading: Electron Pair Geometry Of H2o
Mean Absolute Deviation Calculator Trk
A measure used to find how much the values in a data set vary from their mean is called as the mean absolute deviation. It is also termed as mean deviation or average absolute deviation. It can be calculated by finding the mean of the values first and then find the difference between each value and the mean. Take the absolute value of each difference and find the mean of the difference, which is termed as MAD. Find the MAD of a data set using this mean absolute deviation calculator.
What Is The Median Absolute Deviation
The median absolute deviation is a robust measure of how spread out a set of data is. The variance and standard deviation are also measures of spread, but they are more affected by extremely high or extremely low values and non normality. If your data is normal, the standard deviation is usually the best choice for assessing spread. However, if your data isnt normal, the MAD is one statistic you can use instead.
The Interquartile Range is similar to the MAD, and is a simpler statistic. However, its less robust.
The MAD is defined as:
MAD = median
The formula is a variation of the mean absolute deviation formula . It is less affected by outliers because outliers have a smaller effect on the median than they do on the mean.
The term median absolute deviation refers to a statistic calculated from a sample. However, it can be used to estimate the population parameter.
Read Also: How Does France’s Geography Affect Its Economy
Preparing For Ways Of Thinking
Look for students who understand that the mean absolute deviation is a measure of how spread out the values in a data set are from the mean.
Look for students who make the connection between the mean absolute deviation and the mean, and those that understand that the mean absolute deviation can help determine if the mean is a good indicator of how the data looks. Make note of students who are having trouble understanding how to use the MAD to compare the class data, so you can address any misconceptions during the Ways of Thinking discussion.
How To Find Mad Manually :
The formula for the calculation is discussed earlier, here we have an example:
Example:
Calculate the mean absolute deviation for the data set: 4, 16, 8, 9, 14, 5?
Solution:
$$ MAD = |xi m| / n $$
Here,
Find deviation from the mean:
Determine the mode of each value:
Determine the mean of absolute values:
Also, our mean deviation calculator uses this formula for the calculation of the MAD. For ease, you can also try our online mean mode median calculator that helps you to calculate the mean, mode & median of your given data set.
Also Check: The Molecular Geometry Of The Bro3 Ion Is
What Is The Mean Absolute Deviation
The mean absolute deviation is a measure of variability that indicates the average distance between observations and their mean. MAD uses the original units of the data, which simplifies interpretation. Larger values signify that the data points spread out further from the average. Conversely, lower values correspond to data points bunching closer to it. The mean absolute deviation is also known as the mean deviation and average absolute deviation.
This definition of the mean absolute deviation sounds similar to the standard deviation . While both measure variability, they have different calculations. In recent years, some proponents of MAD have suggested that it replace the SD as the primary measure because it is a simpler concept that better fits real life.
In this post, youll learn how to find and interpret the mean absolute deviation and understand its formula. Ill close by comparing it to the standard deviation.
Why Use Mad And Not Standard Deviation
As we mentioned earlier, MAD and standard deviation are both measures of spread they tell you how much variation there is in your data relative to the mean. So what then is the difference between MAD and standard deviation, and why would you want to use one of these measures over the other?
While MAD measures the average absolute deviation, standard deviation takes the square root of the average squared deviations.
| MAD |
\left | x_i-\bar \right | xix), youll end up with positive deviations for values that are greater than the mean and negative deviations for values that are less than the mean. The negative deviations partially or wholly cancel out the positive deviations, and this interferes with the goal of calculating the average deviation.
MAD and standard deviations deal with the problem of having positive and negative deviations in different ways. When you calculate MAD, you take the absolute value of the deviations, which turns all the deviations positive. When you calculate standard deviation, you square all the deviations, which turns the deviations positive but changes the units of the deviations into squared units. As an added step, when calculating standard deviation, you take the square root of the average square deviations to get the units back into their original form.
Read Also: What Was The Geography And Climate Of New England
Vecdimvector Of Dimensionspositive Integer Vector
Vector of dimensions, specified as a positive integer vector. Each element ofvecdim represents a dimension of the input arrayX. The output y has length 1 in the specified operating dimensions. The other dimension lengths are the same forX and y.
For example, if X is a 2-by-3-by-3 array, thenmad returns a 1-by-1-by-3 array. Each element of the output array is the mean absolute deviation of the elements on the corresponding page ofX.
Data Types: single | double
Mean Absolute Deviation Formula
Average absolute deviation of the collected data set is the average of absolute deviations from a centre point of the data set. Abbreviated as MAD, Mean absolute deviation has four types of deviations that are derived by central tendency, mean median and mode and standard deviation. Mean absolute deviation is, however, best used as it is more accurate and easy to use in real-life situations.
The formula for Mean Absolute Deviation is as follows:
Where
n
To find MAD, you need to follow below steps:
- Calculate the mean for the given set of data.
- Find the difference between each value present in the data set and the mean that gives you the absolute value.
- Find the average of all the absolute values of the difference between the data set and the mean that gives the mean absolute deviation .
Read Also: What Are Norms In Psychological Testing
Mad Using Geometric Median
Analogously to how the median generalizes to the geometric median in multivariate data, MAD can be generalized to MADGM in n dimensions. This is done by replacing the absolute differences in one dimension by euclidian distances of the data points to the geometric median in n dimensions. This gives the identical result as the univariate MAD in 1 dimension and generalizes to any number of dimensions. MADGM needs the geometric median to be found, which is done by an iterative process.
Learning Tricks As An Adult
Also Check: Punchline Bridge To Algebra Why Was The Pail Pale Answers
Example: Mean Absolute Deviation About The Median
Start with the same data set as the first example:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
The median of the data set is 6. In the following table, we show the details of the calculation of the mean absolute deviation about the median.
| Data Value |
| Total of Absolute Deviations: | 22 |
We divide the sum of the absolute deviations and see that we have a mean absolute deviation about the mode of 22/10 = 2.2.
Solved Examples Using Mean Absolute Deviation Formula
Example 1: Find mean absolute deviation for the following data set: 302, 140, 352, 563, 455, 215, 213
Solution:
To find: Mean absolute deviation for the given data set.
Given:
Data set =
Mean of the data = /7 = 320
Using Mean Deviation Formula,
MAD =\
= 117.14
Answer: Mean absolute deviation of the data set is 117.14.
Example 2: For the given data set, if the mean of the dataset is 31. Find the mean absolute deviation of the data set.
30, 14, 35, 55, 45, 21, X
Solution:
To find: Mean absolute deviation of the data set
Given:
Data set =
Mean of the data set = 31
Mean of the data = /7 = 31
200 + X = 31 × 7 = 217
X = 17
Using Mean Deviation Formula,
MAD =\
= 12
Don’t Miss: What Is Plate Tectonics In Geography
How Many Pieces Did My Friends Have
Choose 1 answer
Finally, there is one more case I want to explore. What if we know what a givenfraction of somenumber equals and we need to find that number?
For example, we know my friends had 8 pieces of the birthday cake and that was 2/3 of the whole cake. How many pieces did the cake have in the beginning? In order to find that whole number, we need to divide 8 by 2/3, which is 12.
Solve the next question on your own. A race car drove 900 meters on a track, which is 3/5 of the whole distance. What’s the length of the race track?
Example: Mean Absolute Deviation About The Mean

Suppose that we start with the following data set:
1, 2, 2, 3, 5, 7, 7, 7, 7, 9.
The mean of this data set is 5. The following table will organize our work in calculating the mean absolute deviation about the mean.
| Data Value |
| Total of Absolute Deviations: | 18 |
Thus the mean absolute deviation about the mean is 18/10 = 1.8. We compare this result to the first example. Although the mean was identical for each of these examples, the data in the first example was more spread out. We see from these two examples that the mean absolute deviation from the first example is greater than the mean absolute deviation from the second example. The greater the mean absolute deviation, the greater the dispersion of our data.
Also Check: What Does Interior Mean In Math
Find Mean Absolute Deviation Along Vector Of Dimensions
Find the mean absolute deviation over multiple dimensions by using the vecdim input argument.
Set the random seed for reproducibility of the results.
rng
Create a 4-by-3-by-2 array of random numbers.
X = randn
X = X = 0.5377 0.3188 3.5784 1.8339 -1.3077 2.7694 -2.2588 -0.4336 -1.3499 0.8622 0.3426 3.0349X = 0.7254 -0.1241 0.6715 -0.0631 1.4897 -1.2075 0.7147 1.4090 0.7172 -0.2050 1.4172 1.6302
Find the mean absolute deviation of each page of X by specifying the first and second dimensions.
ypage = mad
ypage = ypage = 1.4626ypage = 0.6652
For example, ypage is the mean absolute deviation of all the elements in X, and is equivalent to specifying mad,0,’all’).
Find the mean absolute deviation of the elements in each X slice by specifying the first and third dimensions.
ycol = mad
ycol = 1Ã3 0.8330 0.7872 1.5227
For example, ycol is the mean absolute deviation of all the elements in X, and is equivalent to specifying mad,0,’all’).
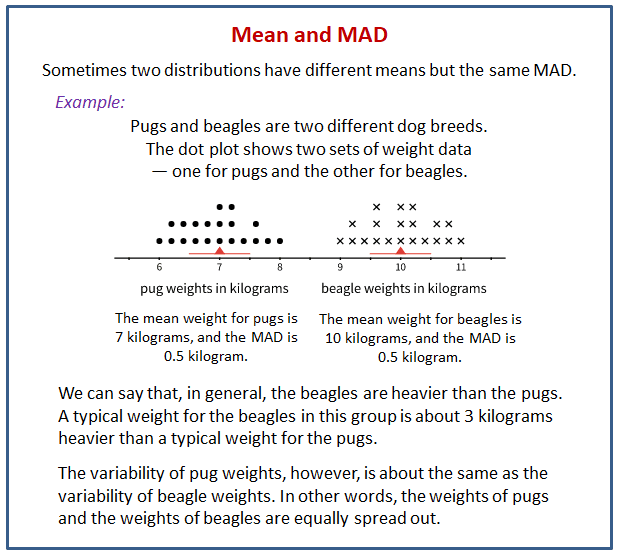
Using Mean And Mad To Make Comparisons
Let’s use mean and MAD to describe and compare distributions.
Exercise \: Number Talk: Decimal Division
Find the value of each expression mentally.
Exercise \: Which Player Would You Choose?
Here are two dot plots that represent the two data sets. The triangle indicates the location of the mean.
| eighth-grade student |
|---|
Are you ready for more?
Recommended Reading: What Is Business Psychology Major