Jcgm : 200: Guide To The Expression Of Uncertainty In Measurement
First, you need to know about the Guide to the Expression of Uncertainty in Measurement, also known as the GUM. It is identified as the JCGM 100:2008 and is available from the BIPM website.
This is the most referenced and used guide for measurement uncertainty. Additionally, it is the guide that influences most of the requirements for ISO/IEC 17025:2017 accreditation. So, you should make sure that you download a copy, save it to your computer, and read it.
What Is Measurement Uncertainty
According to the Vocabulary in International Metrology , measurement uncertainty is a non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information use.
Essentially, measurement uncertainty is an estimated range of values that your measurement result could confidently be within.
Since measurements are actually estimated values based on a systematic process, it is appropriate to estimate the uncertainty associated with the measurement.
Perform Arithmetic Operations With Uncertain Measurements
You May Like: Eoc Fsa Warm Ups Algebra 1 Answers
Confidence: Reporting Uncertainty And Error
As a result of error, scientific measurements are not reported as single values, but rather as ranges or averages with error bars in a graph or ± sign in a table. Karl Pearson first described mathematical methods for determining the probability distributions of scientific measurements, and these methods form the basis of statistical applications in scientific research . Statistical techniques allow us to estimate and report the error surrounding a value after repeated measurement of that value. For example, both Libby and Wu reported their estimates as ranges of one standard deviation around the mean, or average, measurement. The standard deviation provides a measure of the range of variability of individual measurements, and specifically, defines a range that encompasses 34.1% of individual measurements above the mean value and 34.1% of those below the mean. The standard deviation of a range of measurements can be used to compute a confidence interval around the value.
In this case, there is no “theoretically correct” value, but the confidence interval provides an estimate of the probability that a similar result will be found if the study is repeated. Given that Morimoto determined a 95% confidence interval, if he repeated his study 100 times , his confidence interval would overlap the mean pitch speed 95 times, and the other five studies would likely yield pitch speeds that fall outside of his confidence interval.
Comprehension Checkpoint
The Concept Of Measurement Uncertainty
Brief summary: This section introduces the concepts of measurand, true value, measured value, error, measurement uncertainty and probability.
The concept of measurement uncertainty
Measurement is a process of experimentally obtaining the value of a quantity. The quantity that we intend to measure is called measurand. In chemistry the measurand is usually the content of some chemical entity in some object. The chemical entity that is intended be determined is called analyte. Measurands in chemistry can be, for example, lead concentration in a water sample, content of pesticide thiabendazole in an orange or fat content in a bottle of milk. In the preceding example lead , ascorbic acid and fat are the analytes. Water, orange and milk are analysis objects .
In principle, the aim of a measurement is to obtain the true value of the measurand. Every effort is made to optimize the measurement procedure in such a way that the measured value is as close as possible to the true value. However, our measurement result will be just an estimate of the true value and the actual true value will always remain unknown to us. Therefore, we cannot know exactly how near our measured value is to the true value our estimate always has some uncertainty associated with it.
Scheme 1.1. Interrelations between the concepts true value, measured value, error and uncertainty.
Read Also: Why Are There Different Branches Of Chemistry
Significant Figures In Calculations
A second important principle of uncertainty is that results calculated from a measurement are at least as uncertain as the measurement itself. We must take the uncertainty in our measurements into account to avoid misrepresenting the uncertainty in calculated results. One way to do this is to report the result of a calculation with the correct number of significant figures, which is determined by the following three rules for rounding numbers:
The following examples illustrate the application of this rule in rounding a few different numbers to three significant figures:
- 0.028675 rounds up to 0.0287
- 18.3384 rounds down to 18.3
- 6.8752 rounds up to 6.88
- 92.85 rounds down to 92.8
Lets work through these rules with a few examples.
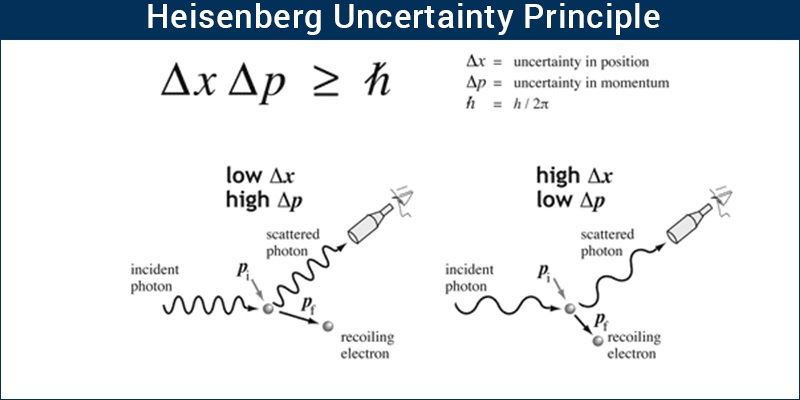
Heisenberg Uncertainty Principle Formula And Application
If, x is the error in position measurement and p is the error in the measurement of momentum, then
X × p
\frac^}}^}} 4×3.14×9.11×10316.626×1034 = 10-4 m2 s-1.
If the position of the electron is measured accurately to its size , then the error in the measurement of its velocity will be equal or larger than 106m or 1000Km.
Heisenberg principle applies to only dual-natured microscopic particles and not to a macroscopic particle whose wave nature is very small.
Also Read: de Broglie Equation
You May Like: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Statistical Vs Systematic Error
As seen in Table 1, an average specific activity value is provided at the bottom with an overall error. The overall error is smaller than the individual error reported with each measurement. This is an important feature of the statistical calculation of error associated with scientific data as you increase the number of measurements of a value, you decrease the uncertainty and increase the confidence associated with the approximation of the value. The error reported alongside of the specific activity provides a measure of the precision of the value, and is commonly referred to as statistical error. Statistical error is what Pearson described as the inherent uncertainty of a measurement. It is caused by random fluctuations within a system, such as the random fluctuation of radioactive , and is sometimes referred to as random error as the researcher has little control over it. Statistical error cannot be eliminated, as Pearson described, but it can be measured and reduced by conducting repeated observations of a specific event.
Figure 3:
| Name of Jin Marquis |
|---|
Is Heisenbergs Uncertainty Principle Noticeable In All Matter Waves
Heisenbergs principle is applicable to all matter waves. The measurement error of any two conjugate properties, whose dimensions happen to be joule sec, like position-momentum, time-energy will be guided by Heisenbergs value.
But, it will be noticeable and of significance only for small particles like an electron with very low mass. A bigger particle with a heavy mass will show the error to be very small and negligible.
You May Like: Are Michael Jackson’s Children Biologically His
Explaining Heisenberg Uncertainty Principle With An Example
Electromagnetic radiations and microscopic matter waves exhibit a dual nature of mass/ momentum and wave character. Position and velocity/momentum of macroscopic matter waves can be determined accurately, simultaneously. For example, the location and speed of a moving car can be determined at the same time, with minimum error. But, in microscopic particles, it will not be possible to fix the position and measure the velocity/momentum of the particle simultaneously.
An electron in an atom has a mass of 9.91 × 10-31Kg. Naked eyes will not see such small particles. A powerful light may collide with the electron and illuminate it. Illumination helps in identifying and measuring the position of the electron. The collision of the powerful light source, while helping in identification increases the momentum of the electron and makes it move away from the initial position. Thus, when fixing the position, the velocity /momentum of the particle would have changed from the original value. Hence, when the position is exact the error occurs in the measurement of velocity or momentum. In the same way, the measurement of momentum accurately will change the position.
Hence, at any point in time, either position or momentum can only be measured accurately.
Simultaneous measurement of both of them will have an error in both position and momentum. Heisenberg quantified the error in the measurement of both position and momentum at the same time.
Uncertainty As A State Of Nature
While Karl Pearson proposed that individual measurements could not yield exact values, he felt that careful and repeated scientific investigation coupled with statistical analysis could allow one to determine the true value of a measurement. A younger contemporary of Pearson’s, the English statistician Ronald Aylmer Fisher, extended and, at the same time, contradicted this concept. Fisher felt that because all measurements contained inherent error, one could never identify the exact or “correct” value of a measurement. According to Fisher, the true distribution of a measurement is unattainable statistical techniques therefore do not estimate the “true” value of a measurement, but rather they are used to minimize error and develop range estimates that approximate the theoretically correct value of the measurement. A natural consequence of his idea is that occasionally the approximation may be incorrect.
Once we understand the concept of uncertainty as it applies to science, we can begin to see that the purpose of scientific dataanalysis is to identify and quantify error and variability toward uncovering the relationships, patterns, and behaviors that occur in nature. Scientific knowledge itself continues to evolve as new data and new studies help us understand and quantify uncertainty in the natural world.
Also Check: What Is The Molecular Geometry Of Ccl4
How Do You Calculate The Uncertainty Of A Measurement
We have studied that scientific measurements differ in their precision and accuracy depending upon the least count of the measuring instrument or scale. In most cases, these results have to be added, subtracted, multiplied, or divided to get the final result. It may be noted that the final computed result cannot be more precise or accurate than the least precise number involved in a particular calculation. The following rules obtain the number of significant figures in such mathematical calculations.
Rule 1: In addition, or subtraction of the numbers having different precisions, the final result should be reported to the same number of decimal places as having the least number of decimal places.
Estimating Uncertainty From A Single Measurement
In many circumstances, a single measurement of a quantity is often sufficient for the purposes of the measurement being taken. But if you only take one measurement, how can you estimate the uncertainty in that measurement? Estimating the uncertainty in a single measurement requires judgement on the part of the experimenter. The uncertainty of a single measurement is limited by the precision and accuracy of the measuring instrument, along with any other factors that might affect the ability of the experimenter to make the measurement and it is up to the experimenter to estimate the uncertainty .
Recommended Reading: Chapter 3 Test Algebra 2 Answers
Uncertainty And Error In Practice: Carbon
Archaeologists, paleontologists, and other researchers have long been interested in dating objects and artifacts in an effort to understand their history and use. Unfortunately, written records are a relatively recent human invention, and few historical artifacts are accompanied by precise written histories.
In the first half of the 20th century, an American nuclear chemist by the name of Willard F. Libby became interested in using the radioactive isotope14C to date certain objects. The theory of radiocarbon dating is relatively simple. Most carbon in the Earth’s atmosphere is in the form of 12C, but a small amount of the isotope 14C is produced naturally through the bombardment of 14N with cosmic rays . As plants take up carbon from the atmosphere through respiration, they incorporate both 14C as well as the more abundant 12C into their tissues. Animals also take up both carbon isotopes through the foods that they eat. Thus, all living organisms have the same ratio of 14C and 12C isotopes in their body as the atmosphere.
In 1949, Libby, working with his post-doctoral student James Arnold, reported the first use of radiocarbon dating for determining the age of wood fragments from archaeological sites around the world . Because the method was new, Arnold and Libby were careful to replicate their measurements to provide a detailed estimate of different types of error, and they compared the results of their method with samples of a known age as a control .
Defining Error And Uncertainty
Some of the terms in this module are used by different authors in different ways. As a result, the use of some terms here might conflict with other published uses. The definitions used in this module are intended to match the usage in documents such as the NIST Reference on Constants, Units and Uncertainty.
For example, the term error, as used here, means the difference between a measured value and the true value for a measurement. Since the exact or “true” measured value of quantity can often not be determined, the error in a measurement can rarely be determined. Instead, it is more consistent with the NIST methods to quantify the uncertainty of a measurement.
Uncertainty as used here means the range of possible values within which the true value of the measurement lies. This definition changes the usage of some other commonly used terms. For example, the term accuracy is often used to mean the difference between a measured result and the actual or true value. Since the true value of a measurement is usually not known, the accuracy of a measurement is usually not known either. Because of these definitions, we modified how we report lab results. For example, when students report results of lab measurements, they do not calculate a percent error between their result and the actual value. Instead, they determine whether the accepted value falls within the range of uncertainty of their result.
Recommended Reading: Lesson 8.1 Practice B Geometry Answers
Sac/singlas Technical Guide : Guide On Measurement Uncertainty In Chemical & Microbiological Measurement
This guide is published by the Singapore Accreditation Council and is not as well known. However, it is a great guide that fills in some the gaps in information left of the EURACHEM guide.
The guide has great examples and include an example of estimating uncertainty for a GC, but could still use more examples. Also, the process for estimating uncertainty is not as defined as the EURACHEM guide. However, it is a great secondary guide that I believe you should add to you reference library.
Recognizing And Reducing Error
Error propagation is not limited to mathematical modeling. It is always a concern in scientific research, especially in studies that proceed stepwise in multiple increments because error in one step can easily be compounded in the next step. As a result, scientists have developed a number of techniques to help quantify error. Here are two examples:
Controls: The use of controls in scientific experiments helps quantify statistical error within an experiment and identify systematic error in order to either measure or eliminate it. Blind trials: In research that involves human judgment, such as studies that try to quantify the perception of pain relief following administration of a pain-relieving drug, scientists often work to minimize error by using “blinds.” In blind trials, the treatment will be compared to a control neither the patient nor the researcher will know if the patient is receiving the treatment or the control. In this way, systematic error due to preconceptions about the utility of a treatment is avoided.
Recommended Reading: Abiotic System Definition
Solved Numerical Problems On Heisenbergs Uncertainty Principle
1. If the position of the electron is measured within an accuracy of + 0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h / 4pm × 0.05 nm, is there any problem in defining this value.
a) x = 2×10-12m X × mV h
12 \,\frac^}}^}}=\frac^}\times 5\times ^}}^}}\,\, 4×1012h×5×1011=4×10126.626×1034×5×1011 = 28 × 10-33
Error in momentum measurement is 1010 times larger than the actual momentum. The given momentum will not be acceptable.
2. Position of a chloride ion on a material can be determined to a maximum error of 1m. If the mass of the chloride ion is 5.86 × 10-26Kg, what will be the error in its velocity measurement?
x = 10-6 m X × mV h
x = 0.12 m