Faqs On Difference Between Linear And Nonlinear Equations
1. How do I know that an equation is a linear or nonlinear equation?
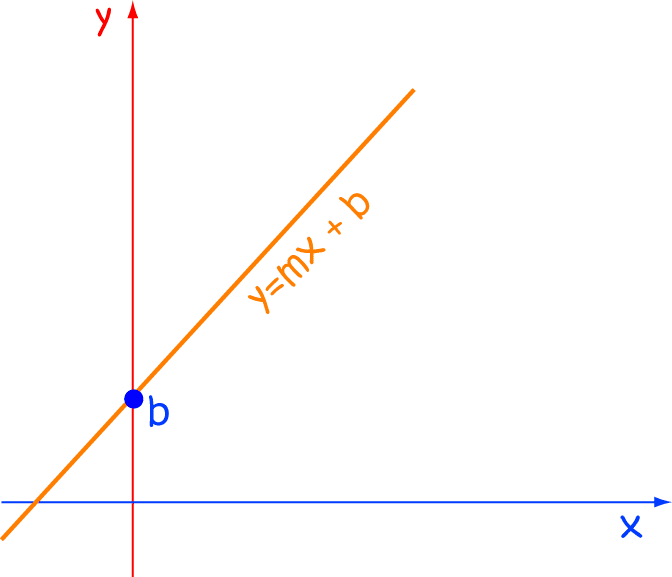
To determine whether the given equation is linear we have to determine that a given equation is in the format
y = mx + c
where m is the slope
x and y are the variables
c is the y-intercept.
For example y = 2x + 1, here the equation has the highest degree as one So it is a linear equation.
A nonlinear equation will not match this equation.
You can also test an equation is linear or nonlinear by plotting it on the graph.
If an equation gives a straight line then that equation is a linear equation.
Example: y = 2x + 1 is the equation can be represented on the graph as
Here it represents a straight line so it is a linear equation.
2. How to solve a linear equation?
To solve a linear equation we use the idea of a balance to find the value of x. We have to keep both the right-hand side and left-hand side balance. We can maintain this status by performing the same operation by on both sides, such as adding subtracting, multiplying, or dividing by the same numbers.
Here are the following steps to solve a linear equation:
Step 1:Start by moving all of the terms that contain a variable to the left-hand side of the equation.
Step 2:Move the terms that do not contain variables to the right-hand side of the equation.
Step 3:Look at the variable and determine if there are any other operations being performed on it. you will get the value.
3. What are some of the features of nonlinear equations?
What Does The Number Line Mean In Math
Number line. Jump to navigation Jump to search. In basic mathematics, a number line is a picture of a graduated straight line that serves as abstraction for real numbers, denoted by R } . Every point of a number line is assumed to correspond to a real number, and every real number to a point.
How are linear equations used in everyday life?
Linear equations use one or more variables where one variable is dependent on the other. Almost any situation where there is an unknown quantity can be represented by a linear equation, like figuring out income over time, calculating mileage rates, or predicting profit.
What does the constant rate mean in math?
A constant rate in math is the absence of acceleration. In general, a function with a constant rate is one with a second derivative of 0. If you were to plot the function on standard graph paper, it would be a straight line, as the change in y would be constant.
System Of Linear Inequalities
A system of linear inequalities in two variables includes at least two linear inequalities in the identical variables. When we solve linear inequality then we get an ordered pair. So basically, in a system, the solution to all inequalities and the graph of the linear inequality is the graph displaying all solutions of the system. Let us see an example to understand it.
Example: Graph the Linear inequality: 2x y > 1, x 2y < 1
Solution: Given two inequality expressions:
2x y > 1 .
We need to find the solution for the given inequalities using a graph.
Let us take first, 2x y > 1
We have to find the points to plot in the graph.
Putting x = 0 in equation and putting = instead of >
y = -1
Again putting y = 0 in equation and putting = instead of >
x = 1/2 = =0.5
Thus, the points are and .
If we put x=0 and y=0, to check for origin, then
0 > 1, which is not true.
Thus, the origin does not lie in the solution of 2x y > 1.
Repeat the same step for equation . Thus the required points will and .
Checking for origin, put x =0 and y = 0.
0 < -1, which is not true.
Thus, the origin does not lie in the solution of x 2y < 1.
Hence, the required solution in the graph will be:
Recommended Reading: What Is Plateau In Geography
Example : Amount Of Water In A Leaky Bucket = Rate Of Leak Time
In this equation, since you won’t ever have a negative amount of water in the bucket, the graph will show points only in the first quadrant. Notice that the direction of the line in this graph is top left to bottom right. Lines that tend in this direction have negative slope. A negative slope indicates that the values on the y-axis are decreasing as the values on the x-axis are increasing.
Real Life Example Of Linear Function
Here are some real-life applications of the linear function.
- A movie streaming service charges a monthly fee of $4.50 and an additional fee of $0.35 for every movie downloaded. Now, the total monthly fee is represented by the linear function f = 0.35x + 4.50, where x is the number of movies downloaded in a month.
- A t-shirt company charges a one-time fee of $50 and $7 per T-shirt to print logos on T-shirts. So, the total fee is expressed by the linear function f = 7x + 50, where x is the number of t-shirts.
- The linear function is used to represent an objective function in linear programming problems, to help minimize the close, or maximize the profits.
Read Also: What Does Hl Stand For In Geometry
Graphing A Linear Function By Finding Two Points
To find any two points on a linear function f = mx + b, we just assume some random values for ‘x’ and substitute these values in the function to find the corresponding values for y. The process is explained with an example where we are going to graph the function f = 3x + 5.
- Step 1: Find two points on the line by taking some random values.We will assume that x = -1 and x = 0.
- Step 2: Substitute each of these values in the function to find the corresponding y-values.Here is the table of the linear function y = 3x + 5.
x 3+5 = 5 Therefore, two points on the line are and .
- Step 3: Plot the points on the graph and join them by a line. Also, extend the line on both sides.
Linear Expressions Vs Linear Equations
The main difference between a linear expression and a linear equation is that the linear equation has an equal sign in the expression.
In the common core, you learn that a linear equation is the same thing as a linear function.
Graphing linear equations relates the y-coordinate to the x-value according to the computation of the expression.
Lets take 2x – y + 3 as an example. This is a linear expression. However, if we were to set the expression equal to something, as in 2x – y + 3 = 0, we would get an equation.
There are different equation forms, the two most common being standard form and slope-intercept form. As a review, linear equations always graph to a straight line.
Here is an example of the linear equation above in standard form: 2x – y = -3
Here is the linear equation in slope-intercept form: y = 2x + 3
On the graph, they both become a straight line:
Also Check: How To Study Geography Maps
Introduction To Linear Algebra
Linear algebra is the study of linear combinations. It is the study of vector spaces, lines and planes, and some mappings that are required to perform the linear transformations. It includes vectors, matrices and linear functions. It is the study of linear sets of equations and its transformation properties.
Linear Algebra Equations
The general linear equation is represented as
a1x1 + a2x2.+anxn = b
as represents the coefficients
xs represents the unknowns
b represents the constant
There exists a system of linear algebraic equations, which is the set of equations. The system of equations can be solved using the matrices.
It obeys the linear function such as
a1x1 +.+anxn
The most important topics covered in the linear algebra includes:
- Euclidean vector spaces
- Singular value decomposition
- Linear dependence and independence
Here, the three main concepts which are the prerequisite to linear algebra are explained in detail. They are:
- Linear Functions
All these three concepts are interrelated such that a system of linear equations can be represented using these concepts mathematically. In general terms, vectors are elements that we can add, and linear functions are the functions of vectors that include the addition of vectors
Graphing A Linear Function Using Slope And Y
To graph a linear function, f = mx + b, we can use its slope‘m’ and the y-intercept‘b’. The process is explained again by graphing the same linear function f = 3x + 5. Its slope is, m = 3 and its y-intercept is = .
- Step 1: Plot the y-intercept .Here, we plot the point .
- Step 2: Write the slope as the fraction rise/run and identify the “rise” and the “run”.Here, the slope = 3 = 3/1 = rise/run.So rise = 3 and run = 1.
- Step 3: Rise the y-intercept vertically by “rise” and then run horizontally by “run”. This results in a new point.Here, we go up by 3 units from the y-intercept and thereby go right by 1 unit.
- Step 4: Join the points from Step 1 and Step 2 by a line and extend the line on both sides.
Read Also: How To Use Foil Math
Difference Between Linear And Nonlinear Equations
We have learned about equations in the earlier classes. An equation is a statement of the equality of two expressions. The two sides of the equality sign are referred to as the left-hand side and the right-hand side of the equation.
For example, in the equation 3x + 4 = 8, where 3, 4, and 8 are the constants, and x is the variable. The LHS is given by the expression 3x + 4 and the RHS is given by the constant 8. The equation remains unchanged if we carry out the same operation on both sides of the equation.
To solve an equation, we carry out a series of identical Mathematical operations on two sides of the equation such that the unknown variable is on one side and its value is obtained on the other side.
Equation: An equation is a statement of equality of two algebraic expressions involving constants and variables.
Based on the degree and variable in the equations, they are classified as linear and nonlinear equations.
Solution Of Linear Equations In Two Variables
There are several methods for solving a linear equation in 2 variables. Some commonly used methods are:
- Method of substitution
- Method of elimination
Substitution Method
We use the substitution method when we have two linear equations with two unknown values. The following steps will help you solve the linear equations.
- Step 1: First, simplify the given equation. Expand the parenthesis.
- Step 2: Now, we will solve one of the equations to obtain the value of either x or y.
- Step 3: Substitute the value of x in terms of y in the other equation or the value of y in terms of x.
- Step 4: Solve the new equation following the basic arithmetic operations rules to find the value of a variable.
- Step 5: Finally, use the value obtained and find the value of the second variable.
Example 2: Calculate the value of x and y from the equations 2x+3y = 13 and x-2y = -4
2x + 3y = 13
Substituting the value of y in eq
x= 2 -4
Cross Multiplication Method
Cross multiplication is one of the simplest methods, and it is applicable only when we are given a pair of linear equations in two variables. We multiply the numerator of one fraction to the denominator of the other. The denominator of the first term is multiplied by the numerator of another term. The following equation is for solving linear equations in two variables using the cross multiplication method.
Elimination Method
The following steps will help you solve a linear equation:
Example 3: Solve the following equations for x and y
Also Check: College Algebra Chapter 1 Study Guide
Pure And Applied Mathematics
Until the 19th century, the development of mathematics in the West was mainly motivated by the needs of technology and science, and there was no clear distinction between pure and applied mathematics. For example, the natural numbers and arithmetic were introduced for the need of counting, and geometry was motivated by surveying, architecture and astronomy. Later, Isaac Newton introduced infinitesimal calculus for explaining the movement of the planets with his law of gravitation. Moreover, most mathematicians were also scientists, and many scientists were also mathematicians. However, a notable exception occurred with the tradition of pure mathematics in Ancient Greece.
In the 19th century, mathematicians such as Karl Weierstrass and Richard Dedekind increasingly focused their research on internal problems, that is, pure mathematics. This led to split mathematics into pure mathematics and applied mathematics, the latter being often considered as having a lower value among mathematical purists. However, the lines between the two are frequently blurred.
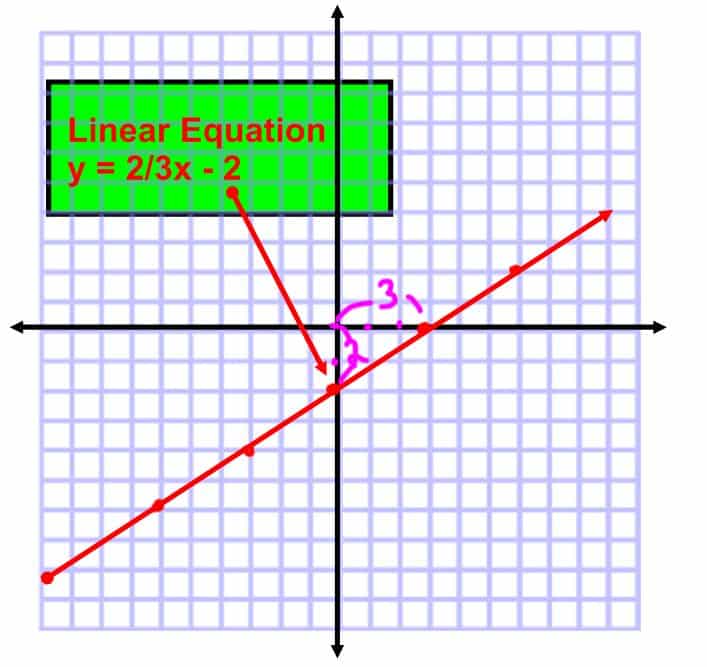
What Is A Linear Equation
An equation that has the highest degree of 1 is known as a linear equation. This means that no variable in a linear equation has an exponent more than 1. The graph of a linear equation always forms a straight line.
Linear Equation Definition: A linear equation is an algebraic equation where each term has an exponent of 1 and when this equation is graphed, it always results in a straight line. This is the reason why it is named as a ‘linear equation’.
There are linear equations in one variable and linear equations in two variables. Let us learn how to identify linear equations and non-linear equations with the help of the following examples.
| Equations | |
|---|---|
| Non-Linear, the power of the variable x is 2 | |
| y + x = 6 | Non-Linear, the power of the variable y is 1/2 |
| y + 3x – 1 = 0 | |
| Non-Linear, the power of the variable y is 2 |
Also Check: Example Of Theorem In Geometry
Statistics And Other Decision Sciences
The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments. The design of a statistical sample or experiment determines the analytical methods that will be used. Analysis of data from observational studies is done using statistical models and the theory of inference, using model selection and estimation. The models and consequential predictions should then be tested against new data.
Statistical theory studies such as minimizing the risk of a statistical action, such as using a procedure in, for example, parameter estimation, hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing an objective function, like expected loss or cost, under specific constraints. For example, designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence. Because of its use of optimization, the mathematical theory of statistics overlaps with other , such as operations research, control theory, and mathematical economics.
What Is The Formula For Solving Linear Equations
Ans. Linear equations are equations that have variables on both sides, and the variables are all multiplied by a constant. We can solve them by dividing both sides by the constant. For example, if you have an equation with 2x + 3 = 5 then you can solve it by dividing both sides by 2. This will give you x + 3/2 = 5/2 and then dividing both sides again gives you x = 5/4.
Recommended Reading: Who Is Khloe Kardashian’s Biological Father
What Is A Vertex In Math
In mathematics, particularly graph theory, the fundamental component of a graph is referred to as a vertex , however, it is also referred to as a node. A directed graph is made up of a set of vertices and a set of arcs, whereas an undirected graph is made up of a set of vertices and a set of edges . An arc connects two vertices in a directed graph . In a diagram of a graph, a vertex is often represented by a circle with a label, and an edge is typically represented by a line or arrow that connects two of the diagram’s vertex points.
From the standpoint of graph theory, vertices are seen as featureless and indivisible objects, even though they could have an extra structure based on the application that spawned the graph. For instance, a semantic network is a graph in which the vertices represent different ideas or groups of things.
The edge is said to be incident to the vertices and to have the two vertices creating it as its ends. If there is an edge in the graph, a vertex w is considered to be close to a vertex v. . The vertices around a vertex together constitute the neighborhood of that vertex, which is an induced subgraph of the graph.
Differentiate Between Linear And Nonlinear Equations
|
Linear Equations |
Non-Linear Equations |
|
A Linear equation can be defined as the equation having a maximum of only one degree. |
A Nonlinear equation can be defined as the equation having the maximum degree 2 or more than 2. |
|
A linear equation forms a straight line on the graph. |
A nonlinear equation forms a curve on the graph. |
|
The general form of linear equation is, y = mx +c Where x and y are the variables, m is the slope of the line and c is a constant value. |
The general form of nonlinear equations is, ax2 + by2 = c Where x and y are the variables and a,b and c are the constant values |
|
Examples: |
Let us understand what are linear and nonlinear equations with the help of some examples.
Also Check: Does Doing Math Increase Iq