Domain: Grade 10 > > Geometry Congruence
Sample Question: What would be the coordinates of point S after applying the following rule: ?
Answer Explanation: Answer: A
Although they are congruent angles, the question is asking for the property. Since they are in corresponding locations with the transversal the correct answer is A
Click here to practice: Geometry Similarity, Right Triangles, & Trigonometry Questions for Grade 10 Math
Algebra Practice Problems Worksheet For Grade 10
Solve = y z = 2x 11 = 9
One hundred and fifty students are admitted to a school. They are distributed over three sections A, B and C. If 6 students are shifted from section A to section C, the sections will have equal number of students. If 4 times of students of section C exceeds the number of students of section A by the number of students in section B, find the number of students in the three sections. Solution
In a three-digit number, when the tens and the hundreds digit are interchanged the new number is 54 more than three times the original number. If 198 is added to the number, the digits are reversed. The tens digit exceeds the hundreds digit by twice as that of the tens digit exceeds the unit digit. Find the original number.
Find the least common multiple of xy+k and xy+k Solution
Find the GCD of the following by division algorithm
2×4 +13×3 +27×2 + 23x + 7 , x3 + 3×2 + 3x + 1 , x2 + 2x + 1
Reduce the given Rational expressions to its lowest form
/ Solution
/ Solution
Simplify
Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone? Solution
Find the square root of 289×4 612×3 + 970×2 684x + 361. Solution
Solve + = 3 Solution
Is it possible to design a rectangular park of perimeter 320 m and area 4800 m2 ? If so find its length and breadth. Solution
Domain: Grade 10 > > Number And Quantity The Real Number System
Sample Question: Evaluate 9 150/300
Answer Explanation: 9150/300 = 91/2 = square root of 9 = 3. In a problem with a rational exponent, the numerator tells you the power, and the denominator the root. However, in this problem the exponent can be reduced, so we should reduce that first. The exponent 150/300 = 1/2. So the problem becomes 9 to the 1/2 power. The denominator is 2 so we take the square root of 9 which is 3. The numerator is 1 so we raise 3 to the 1st power and the answer is 3.
Also Check: How To Avoid Parallax Error In Physics
Overview Of Act Math Algebra
The ACT Math Test consists of 60 multiple-choice questions to be answered within 60 minutes. The test assesses math skills that students typically learn up until the beginning of their senior year of high school. A calculator is allowed for the math portion of the ACT, however, all questions are able to be solved without the use of one.
Algebra questions comprise 12-15% of the math test and tests students on their ability to solve, graph and model different types of expressions. Students are expected to be able to manipulate linear, polynomial, radical and exponential relationships as well as finding solutions to systems of equations .
Not only will you be given an overall score for the ACT Math Test, but you will also receive subscores for each of the subsections in the Math test. The ACT also provides the following directions for the math section of the exam which we recommend you become familiar with prior to taking the exam:
Grade 10 Math Questions And Solutions

The Smarter Balanced Assessment Consortium is a standardized test that includes a variety of new technology-enhanced questions.
Some of them are Multiple choice-single correct responses, Multiple choice-multiple correct responses, Matching Tables, Drag and Drop, Hot text, Table Fill in, Graphing, Equation/numeric, Extended constructed response, Short answer, and many more.
This page contains several sample questions along with practice test links for Grade 10 Math that gives you an idea of questions that your students are likely to see on the test. After each sample question, an answer explanation follows. The explanation includes essential aspects of the task that you may need to consider for the skills, processes, and information your students need to know.
You May Like: Algebra 2 Eoc Fsa Practice Test
Domain: Grade 10 > > Statistics & Probability Using Probability To Make Decisions
Sample Question:Using just the Venn diagram above, find P.
Answer Explanation: Simply count the data points in circles C and E. There are 8 of them out of 24 total data points and by reducing we get 8/24=1/3.
Click here to practice: Statistics & Probability Using Probability to Make Decisions Questions for Grade 10 Math
Domain: Grade 10 > > Geometry Modeling With Geometry
Sample Question: A company ships spherical paperweights in cubic boxes. The circumference of the paperweight is 9 cm. If the box fits the sphere exactly with the sides of the sphere touching the box, what is the volume of the smallest box the company can use for shipping.
Click here to practice: Geometry Modeling with Geometry Questions for Grade 10 Math
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Domain: Grade 10 > > Statistics & Probability Interpreting Categorical & Quantitative Data
Sample Question: Given the scatter plot below, what type of function expresses the correlation between the two variables?
Answer Explanation: Notice that the trend of the graph between the data points forms a line.
Click here to practice: Statistics & Probability Interpreting Categorical & Quantitative Data Questions for Grade 10 Math
How To Solve Algebraic Expression
The purpose of solving an algebraic expression in an equation is to find the unknown variable. When two expressions are equated, they form an equation, and therefore, it becomes easier to solve for the unknown terms.
To solve an equation, place the variables on one side and the constants on the other side. You can isolate the variables by applying arithmetic operations like addition, subtraction, multiplication, division, square root, cube root, etc.
An algebraic expression is always interchangeable. This implies that you can rewrite the equation by interchanging the LHS and RHS.
Calculate the value of x in the following equation
5x + 10 = 50
Given Equation as 5x + 10 = 50
- Isolate the variables and the constants
- You can keep the variable on the LHS and the constants on the RHS.
5x = 50-10
Also Check: Elastic Force Definition Physics
Domain: Grade 10 > > Geometry Circles
Sample Question: What is the translation rule and the scale factor of the dilation as Circle FCircle F ?
Answer Explanation: The original circle F has its center at the point with a radius of 4 units. The translated/dilated circle F has its center at the point with a radius of 1 units. This means the center was translated up 10 units. As a transformation, this translation is written as . Circle F was also dilated by a factor of 1/4 because the radius was reduced from 4 units to 1 units. As a transformation, this dilation is written as 1/4. Putting the translation and dilation together, the rule is 1/4.
Standards:
Click here to practice: Geometry Circles Questions for Grade 10 Math
Example Question #: Algebra
Let x be a number. Increasing x by twenty percent yields that same result as decreasing the product of four and x by five. What is x?
Possible Answers:Correct answer:
The problem tells us that increasing x by twenty percent gives us the same thing that we would get if we decreased the product of four and x by five. We need to find expressions for these two situations, and then we can set them equal and solve for x.
Let’s find an expression for increasing x by twenty percent. We could represent this as x + 20%x = x + 0.2x = 1.2x = 6x/5.
Let’s find an expression for decreasing the product of four and x by five. First, we must find the product of four and x, which can be written as 4x. Then we must decrease this by five, so we must subtract five from 4x, which could be written as 4x – 5.
Now we must set the two expressions equal to one another.
6x/5 = 4x – 5
Subtract 6x/5 from both sides. We can rewrite 4x as 20x/5 so that it has a common denominator with 6x/5.
0 = 20x/5 – 6x/5 – 5 = 14x/5 – 5
0 = 14x/5 – 5
Now we can add five to both sides.
5 = 14x/5
Now we can multiply both sides by 5/14, which is the reciprocal of 14/5.
5 = = x
If 4xs = v, v = ks , and sv 0, which of the following is equal to k ?
Possible Answers:
Read Also: Algebra 1 Age Word Problems
Algebra Questions For Class 6
Basic algebra deals with finding the unknown value using variables.
1. Soldiers are marching in a parade. There are 10 soldiers in a row. What is the rule which gives the number of soldiers, given the number of rows?
Solution: Let n be the number of rows
Number of soldiers in a row = 10
Total number of soldiers = number of soldiers in a row × number of rows
= 10n
2. Leela is Radhas younger sister. Leela is 4 years younger than Radha. Write Leelas age with respect to Radhas age. Take Radhas age to be x years.
Solution: Let Radhas age be x years
Leelas age = 4 years younger than Radha
= years
3. If a is the side-length of the equilateral triangle, then the perimeter of the triangle will be?
Solution: Side of equilateral triangle = a
The perimeter of triangle = sum of all its three sides
Since we know that an equilateral triangle has all its sides equal.
Therefore,
Perimeter of equilateral triangle = a+a+a = 3a
4. Give expressions for:
p multiplied by 7
p divided by 7
Solution:
p multiplied by 7
P×7 = 7p
p divided by 7
P÷7 = p/7
5. If Sam age is x years. Then, what is the age of Sam after 7 years?
Solution: Sams present age = x
After 7 years,
Algebraic Expression Explanation & Examples
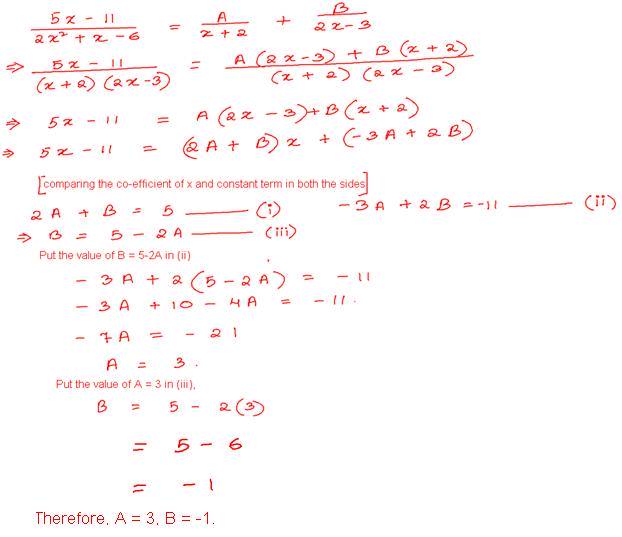
Algebra is an interesting and enjoyable branch of mathematics in which numbers, shapes, and letters are used to express problems. Whether you are learning algebra in school or examining a certain test, you will notice that almost all mathematical problems are represented in words.
Therefore, the need to translate written word problems into algebraic expressions arises when we need to solve them.
Most of the algebraic word problems consist of real-life short stories or cases. Others are simple phrases such as the description of a math problem. This article will learn how to write algebraic expressions from simple word problems and then advance to lightly complex word problems.
Read Also: Geometry Dash Demon Key Hack
Addition And Subtraction Of Algebraic Expression
6. Collect like terms and simplify the expression:
12m2 9m + 5m 4m2 7m + 10
Solution: Rearranging terms, we have:
12m2 4m2 + 5m 9m 7m + 10
= m2 + m + 10
= 8m2 + m + 10
= 8m2 + m + 10
7. Subtract 24ab 10b 18a from 30ab + 12b + 14a.
Solution: 30ab + 12b + 14a
= 30ab + 12b + 14a 24ab + 10b + 18a
= 30ab 24ab + 12b + 10b + 14a + 18a
= 6ab + 22b + 32a
8. Find the value of x2-5x+8, for x = 2.
Solution: Given: x2-5x+8
= 2 5 + 8
Grade 10 Algebra Question
Simplify the following:$\left \left \div 4^$ I don’t know how to simplify this expression.
- 1$\begingroup$$8^=\Big^$ $=2^$ $=2^$. And just as $8$ is $2^3$, so $16$ is $2^4$ and $4$ is $2^2$. $\qquad$$\endgroup$
Hint: Use that$$4=2^2\qquad 8=2^3\qquad 16=2^4$$as well as these rules about exponentiation:$$^c=a^\qquad a^b\div a^c=a^$$
Note that:$$8^=\left^=2^$$$$16^=\left^=2^$$$$4^=\left^=2^$$
Since they are all raised to the same base $$ you can go ahead and apply the relevant exponential laws to simplify your expression. Namely $a^na^m=a^$ to simplify the numerator and $\frac=a^$ to further simplify the remaining expression.
Read Also: Theory Of Everything 2 Music
Domain: Grade 10 > > Functions Trigonometric Functions
Sample Question: In the unit circle, one can see that tan=1 . What is the value of cos?
Answer Explanation:The trigonometric ratio of cosine is the ratio of the length of the adjacent side divided by the length of the hypotenuse. The length of the adjacent side is the xvalue in a point on the unit circle. The hypotenuse is the radius of the unit circle, so the hypotenuse is 1. Thus, the value of the cosine ratio of any angle in the unit circle is the xvalue of the point on the unit circle that corresponds to that angle. The trigonometric ratio of tangent is the length of the opposite side divided by the length of the adjacent side. The length of the opposite side is the yvalue in a point on the unit circle and the length of the adjacent side is the xvalue in a point on the unit circle. The hypotenuse is the radius of the unit circle, so the hypotenuse is 1. Thus, the value of the tangent ratio of any angle in the unit circle is the ratio yx from the point on the unit circle that corresponds to that angle. In this question, tan=1. This ratio is taken from the point that corresponds to the angle with a measure of 5/4 radians. Thus, using the information above, the value of cos is the same as the xvalue in the point .Therefore, the value of cos=2/2.
Click here to practice: Functions Trigonometric Functions Questions for Grade 10 Math
Domain: Grade 10 > > Number And Quantity Quantities
Sample Question: Rewrite x1/2 in radical form.
Answer Explanation: In a problem with a rational exponent, the numerator tells you the power, and the denominator the root. Since the problem is, x1/2, the denominator is 2 indicating we should take a square root and the numerator is 1 so we would raise that to the first power or there will be no exponent since an exponent of 1 is rarely used. That makes the answer the square root of x, written as x.
Recommended Reading: Geometry Segment Addition Postulate Worksheet
Domain: Grade 10 > > Algebra Arithmetic With Polynomials & Rational Expressions
Sample Question: Evaluate f=a3+6a7 at a = 1 and state the remainder.
Answer Explanation: student must substitute 1 into the function as follows 3+67=12 and find the value to get the remainder
Click here to practice: Algebra Arithmetic with Polynomials & Rational Expressions Questions for Grade 10 Math
Domain: Grade 10 > > Geometry Expressing Geometric Properties With Equations
Sample Question: What value on the number line in the figure below divides segment EF into two parts having a ratio of their lengths of 3:1?
Answer Explanation: Point E is at -7 on the number line in the figure, and pointF is at 1. Thus, the length of segment EF is 8. To divide the segment into two parts with a ratio of their lengths of 3:1, change the ratio to 3x:1x to allow variation in the location on the number line. Next, set the sum of the two parts equal to 8 and solve for x. 3x+1x=8 4x=8 x=2.Now, that you know that x=2, find 3x, which equals 6. Find the value on the number line by adding 6 to the position of point E. 7+6=1.The value on the number line that divides segment EF in a ratio of 3:1 is -1.
Answer Explanation: Use the formula for volume of a pyramid:
V=1/2.a.c.h
In this case the length is 15cm, the base is 10 cm in length, and the height is 9 cm. Therefore :
V=1/2.15.10.9=675cm3
Click here to practice: Geometry Geometric Measurement & Dimension Questions for Grade 10 Math
Read Also: Who Are Paris Jackson’s Biological Parents
Q Bank: Grade 10 Exam Questions And Answers
You can download the past Grade 10 exam papers here for free and without the need to use a password. !
You can also donwload a full compilation of 2010 2014 Grade 10 Exam Questions below click in the image. The Booklet contains questions laid out under each Grade 10 Topic and Answers.
We also have some really good Grade 10 Algebra exam questions. Check them out.
The Grade 10 Q Bank contains exam questions arranged by the Core Grades 9 and 10 Mathematics Units in the PNG school syllabus. We hope that this will make revision effective. The resources are made available to complement the learning resources the mathematics teachers may provide at school.
Domain: Grade 10 > > Algebra Reasoning With Equations & Inequalities
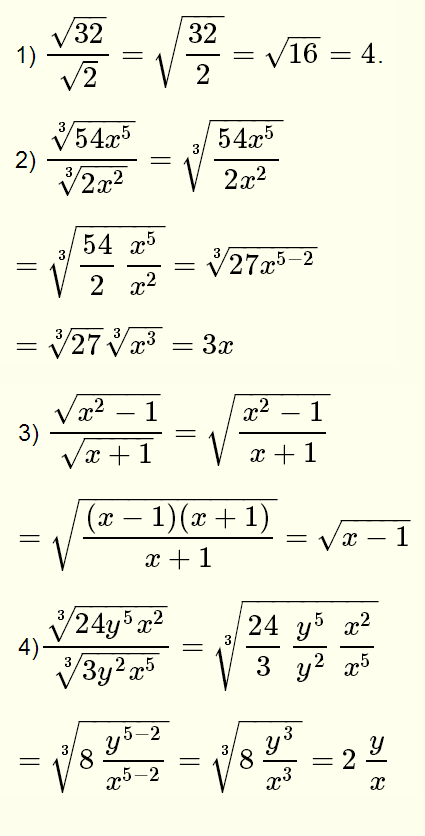
Sample Question: Solve the quadratic x2+10x=25.
Answer Explanation: This problem can be easily solved by rearranging the equation so that it is solved for zero and then factoring as shown:
x2+10x=25
x2+10x+25=0
Since both factors are exactly the same, you will only have one solution to this problem.
x+5=0
Don’t Miss: Fsa Algebra 1 Eoc Answers
Hard Algebra Questions Answers For Competitive Exams
Hard algebra questions answers for competitive exams, practice set 22 specially for SSC CGL. Take the test, verify answers and clear doubts from solutions.
Take the timed test, score your performance from the answers and then clear doubts from the solution set. Link is at the end.
Answering quantitative algebra questions is not the same as in a school test. Quick and correct answer is the key to success in such exams. You will have maximum 1 minute to 90 seconds for answering a question.
Speed of answer, accuracy and strategy are the three key elements for success in any MCQ test.
If you want to skip the following TIPS FOR QUICK ANSWERING and take the test right away click here.