Representing A Linear Equation On X
To understand how to represent a linear equation on the graph using the X- and Y-axis,
let us consider a linear equation, y = x + 1.
Now, lets build a table to represent the corresponding values of y for different values of x and create their ordered pairs:
| x |
The next step is to plot these ordered pairs on the coordinate plane graph.
As a final step, we will join these points to form a straight line and that will be the representation of the equation y = x + 1.
What Value Of Y In Math
Y is just a variable. It depends how it is used.
5y-15=30 well y=9
In a graph you have coordinates also know as an ordered pair.
Standard Form Ax + By = C where A and B are not both equal to zero, A, B, and C are integers whose greatest common factor is 1, and A is nonnegative . The standard form can be converted to the general form, but not always to all the other forms if A or B is zero.
Slope intercept form y= m x+b where m is the slope of the line and b is the y-intercept, which is the y-coordinate of the point where the line crosses the y axis.
Point Slope Form y-y1=m where m is the slope of the line and is any point on the line.The point-slope form expresses the fact that the difference in the y coordinate between two points on a line is proportional to the difference in the xcoordinate . The proportionality constant is m .
Functions where y = f this is for mapping data A function is a relation in which no two ordered pairs have the same x-coordinate when graphed.
All depends on how the Y is being used and Y can be used many ways.
What Is A Linear Equation
Just like any other equation, a linear equation is made up of two expressions set equal to each other. There are some key features common to all linear equations:
A linear equation in two variables can be described as a linear relationship between x and y, that is, two variables in which the value of one of them depends on the value of the other one . In this case, x is the independent variable, and y depends on it, so y is called the dependent variable.
Whether or not it’s labeled x, the independent variable is usually plotted along the horizontal axis. Most linear equations are functions. In other words, for every value of x, there is only one corresponding value of y. When you assign a value to the independent variable, x, you can compute the value of the dependent variable, y. You can then plot the points named by each pair on a coordinate grid.
Also Check: Page 184 Geometry Book Answers
Example : Number Of Angles Of A Polygon = Number Of Sides Of That Polygon
Again in this graph, we are relating values that only make sense if they are positive, so we show points only in the first quadrant. Moreover, in this case, since no polygon has fewer than 3 sides or angles and the number of sides or angles of a polygon must be a whole number, we show the graph starting at and indicate with a dashed line that points between those plotted are not relevant to the problem.
What Is Y In Algebra
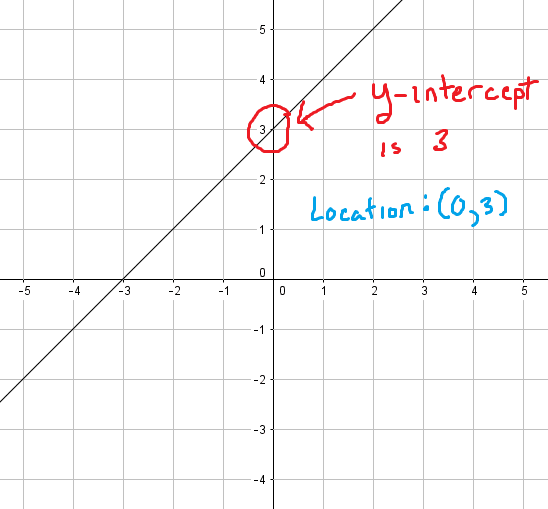
Answer:
unknown number
The symbol stands for an unknown number, the symbol y stands for an unknown number and the symbol 2 stands for a known number, two. In algebra when two symbols that stand for a number are placed beside each other the operation between them is taken to be multiplication.
Step-by-step explanation:
What is y in Algebra?
The letter ‘y’ is a variable in Algebra.
Algebra is a branch of mathematics that deals with symbols and rules for manipulating those symbols. Algebra involves algebraic expressions or manipulating equations. Studying algebra helps you to think logically and critically to solve many problems both in studies and in real-life situations.
You May Like: What Is Cro In Physics
Basic Mathematical Symbols With Name Meaning And Examples
The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.
| Symbol |
|---|
Example : Distance = Rate Time
In this equation, for any given steady rate, the relationship between distance and time will be linear. However, distance is usually expressed as a positive number, so most graphs of this relationship will only show points in the first quadrant. Notice that the direction of the line in the graph below is from bottom left to top right. Lines that tend in this direction have positive slope. A positive slope indicates that the values on both axes are increasing from left to right.
Recommended Reading: What Is The Definition Of Human Geography
Translating Words Into Mathematical Expressions
In this section we turn our attention to translating word phrases into mathematical expressions. We begin with phrases that translate into sums. There is a wide variety of word phrases that translate into sums. Some common examples are given in Table \, though the list is far from complete. In like manner, a number of phrases that translate into differences are shown in Table \.
| Phrase | |||
|---|---|---|---|
| sum of x and 12 | x + 12 | difference of x and 12 | x 12 |
| a) Phrases that are sums | b) Phrases that are differences |
Lets look at some examples, some of which translate into expressions involving sums, and some of which translate into expressions involving differences.
Example 1
Translate the following phrases into mathematical expressions:
Exercise
Translate the following phrases into mathematical expressions:
-
y 12
Example 2
Let W represent the width of the rectangle. The length of a rectangle is 4 feet longer than its width. Express the length of the rectangle in terms of its width W.
Solution
We know that the width of the rectangle is W. Because the length of the rectangle is 4 feet longer that the width, we must add 4 to the width to find the length.
Thus, the length of the rectangle, in terms of its width W, is 4 + W.
Exercise
- Answer
-
L 5
Example 3
How Is A Function Evaluated At A Number
You evaluate “f ” in exactly the same way that you’ve always evaluated “y” namely, you take the number they give you for the input variable, you plug it in for the variable, and you simplify to get the answer. For instance:
-
Given f = x2 + 2x 1, find f .
To evaluate f at x = 2, I’ll plug 2 in for every instance of x in the function’s rule:
f = 2 +2 1
To keep things straight in my head , I’ve put parentheses around every instance of the argument 2 in the formula for f. Now I can simplify:
2 + 2 1
Then my answer is:
f = 2
If you experience difficulties when working with negatives, try using parentheses as I did above. Doing so helps keep track of things like whether or not the exponent is on the “minus” sign. And it’s just generally a good habit to develop.
Affiliate
An important type of function is called a “piecewise” function, so called because, well, it’s in pieces. For instance, the following is a piecewise function:
As you can see, this function is split into two halves: the half that comes before x = 1, and the half that goes from x = 1 to infinity. Which half of the function you use depends on what the value of x is. Let’s examine this:
-
Given the function f as defined above, evaluate the function at the following values: x = 1, x = 3, and x = 1.
This function comes in pieces hence, the name “piecewise” function. When I evaluate it at various x-values, I have to be careful to plug the argument into the correct piece of the function.
f = 22 1
= 2 1
= 2 1 = 1
Recommended Reading: What Is The Definition Of Unit Rate In Math
What Does Y Mean In Math
What does y mean in Math?
In math, y is generally used as an unknown variable. we use y as a variable just like x .
x is also used as a variable in Algebra
y holds the place of a number that we may not know just yet in pre-algebra. We use this symbol when we dont know how many we have of something or when the number of them can change.
y + 4 means we add 4 to whatever we decide y stands for. y could be any number, so were just holding its place with the variable
Why Is The Input To A Function Called The Argument
The term “argument” has a long history. Originally, it was a logical term, referring to a statement that forwarded a proof or, in a less formal sense, a claim that was being used to try to convince somebody of something. Eventually, the term came to refer, in early scientific contexts, to any mathematical value that was needed as an input to other computations, or any value upon which later results depended.
In the twentieth century, when computer coding started becoming a thing, coders adopted the mathematical meaning to refer to inputs to their coding. In our mathematical context, the “argument” is the independent variable and the function’s output is the dependent variable .
-
Given h, what is the function name, and what is the argument?
I’ll do the second part first. The argument is whatever is inside the parentheses, so the argument here is s.
The function name is the variable that comes before the parentheses. In this case, then, the function name is h.
function name: h
argument: s
-
What is the argument of f ?
The argument is whatever is plugged in. In this particular case, the variable being plugged in is “y“. So:
the argument is y
-
Given g = t 2 + t, what is the function name? In g, what is the argument?
The function name is what comes before the parentheses, so the function name here is g.
function name: g
argument of g: 1
Content Continues Below
Read Also: What Is Succession In Biology
Plotting Points On X And Y Axis
Let us learn how to plot a point on the graph by using the X- and Y-axis.
For example: Lets try to plot the point B on the graph.
Here, the x-coordinate of B is 3. So we will start from the origin and move 3 units to the right on x-axis.
Now, the y-coordinate of B is 4, so we will go 4 spaces up from this point.
And thus we have plotted our point B on the graph using the axes.
Example : Amount Of Water In A Leaky Bucket = Rate Of Leak Time
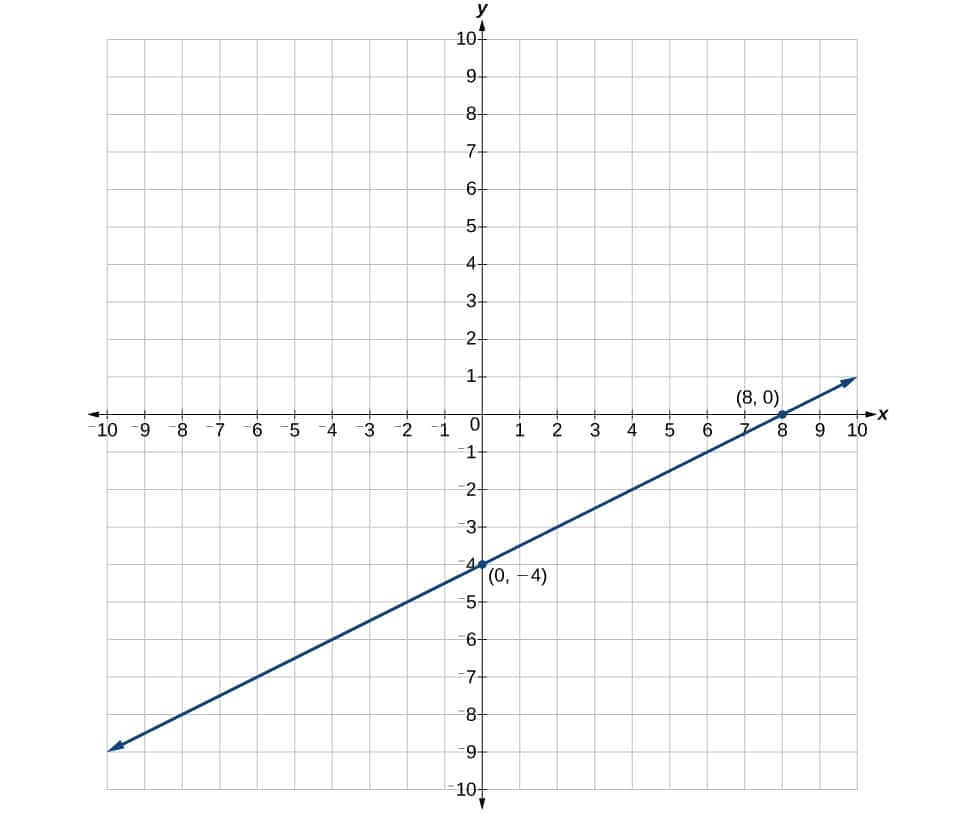
In this equation, since you won’t ever have a negative amount of water in the bucket, the graph will show points only in the first quadrant. Notice that the direction of the line in this graph is top left to bottom right. Lines that tend in this direction have negative slope. A negative slope indicates that the values on the y-axis are decreasing as the values on the x-axis are increasing.
Recommended Reading: Holt Algebra 2 Chapter 2 Test Answers
Teaching Linear Equations In Math
For many students in Grades 8 and up, the numbers and shapes they’ve learned about really start to come together when they are making and solving linear equations. This topic integrates ideas about algebra, geometry, and functions and can be difficult for many childrenand adults!to wrap their heads around. This article explains what a linear equation is and walks through different examples. Then it offers lesson ideas for introducing and developing the concept of linear equations in one variable to your students.