What Is A Unit Rate In Math
Your students have no doubt encountered rates and ratios before , but it may help them to review these concepts before solving problems that use them.
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b 0.
Prerequisite Skills and Concepts: Students should have a basic understanding of ratios, how to write them, and an ability to simplify a ratio. Students should also have an ability to work with fractions and find equivalent fractions.
How To Calculate Unit Rate
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 17 people, some anonymous, worked to edit and improve it over time. This article has been viewed 145,252 times.
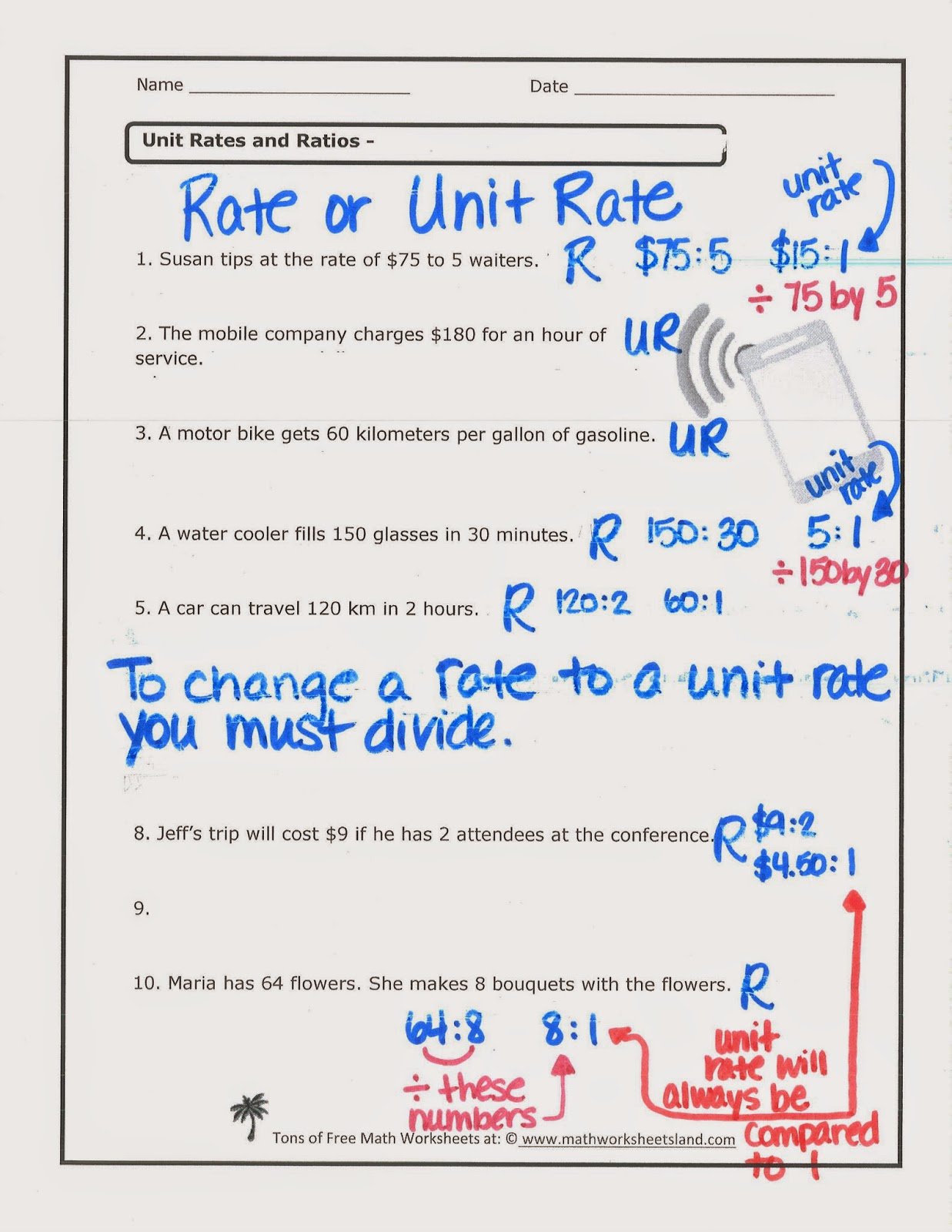
Unit rate is a comparison of any two separate but related measurements when the second of these measurements is reduced to a value of one. Calculating the unit rate in any set of circumstances will require the use of division.
What Is The Definition Of Rate
When two quantities of different units are compared and expressed as a ratio, we refer to it as ‘Rate’. For example, the distance traveled in a particular amount of time is expressed as ‘total distance/time taken to travel’. If 100 miles are traveled in one hour, then we express it as 100 miles per hour. The word ‘per’ or the symbol ‘/’ is used to denote rate.
You May Like: Geometry Mcdougall Littell Answers
What Is The Definition Unit Rate In Math
4.5/5rateunitsrateratesunit rates
Herein, what is the definition of a unit rate?
A rate is a ratio that is used to compare different kinds of quantities. A unit rate describes how many units of the first type of quantity corresponds to one unit of the second type of quantity. Some common unit rates are miles per hour, cost per item, earnings per week, etc.
Similarly, what are examples of unit rate? A unit rate is a rate where the second quantity is one unit , such as $34 per pound, 25 miles per hour, 15 Indian Rupees per Brazilian Real, etc. Example 1: A motorcycle travels 230 miles on 4 gallons of gasoline. Find the average mileage per gallon.
Also to know is, what is the definition of rate in math?
In mathematics, a rate is the ratio between two related quantities in different units. In describing the units of a rate, the word “per” is used to separate the units of the two measurements used to calculate the rate .
How do you find the unit rate in math?
To find the unit rate, divide the numerator and denominator of the given rate by the denominator of the given rate. So in this case, divide the numerator and denominator of 70/5 by 5, to get 14/1, or 14 students per class, which is the unit rate.
What Is A Unit Rate

So what is a unit rate? It is the same thing but with the second number equal to 1. Or, if you prefer a more scientific unit rate definition, it is a way to translate the rate as we have it into the equivalent fraction with the denominator1. After all, it might be useful to know that the 21 dog treats per week translate to three treats a day.
As we’ve seen, ratios and rates are connected, but it’s quite impossible to say that one is better than the other. They’re just different. To convince yourself of that, recall how a map scale is always given in form 1 : 30,000,000, which is a ratio, while we measure the density of objects in ounces per cubic inch , which is a rate. The latter is a unit rate example, and, in fact, most of physics is.
Now that we have the unit rate definition out in the open, it’s time to see how to find this unit rate. The doggy example above should have got the idea through to you, but, nevertheless, why don’t we commit a whole section to describe it in detail?
Don’t Miss: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate
Benefits Of Using Unit Rate In Mathematics:
There exist a lot of different benefits of using Unit Rate in Mathematics, and some of them can be listed as below:
Identifies and Compares Variation in Equations: As we all know that different equations have different frameworks, and all of them should be equally considered so that the result of the Mathematical problem becomes positive and approachable. This is made possible to a much quicker extent with the help of unit rate. A unit rate can measure the approximation of similarity as well as the difference between 2 units and can result in making them successful for the people solving these problems or equations for sure.
The Calculations Become Less Risky & Tough: The toughness of approximation and detection is greatly reduced with the help of unit rate, and this is the most important benefit of this rating in the first place.
The riskiness of all these calculations is primarily reduced, and the extent is quite enlarged with the help of unit rate, and that is why Mathematics has a lot for unit rate and its usage in the initial place and that too undoubtedly.
Unit Rate Examples: Using The Unit Rate Calculator
You’re finally able to make your dream come true – you’re going on a road trip! The plan is to get there , and, once you’ve landed, find a car to rent and visit a few places in one week.
All in all, you want to visit four cities, call them A, B, C, and D, so you have three trips to make between them: A -> B, B -> C, and C -> D. From what you found on the net, the distances are 80 mi, 140 mi, and 110 mi respectively. Also, your GPS tells you that the drives should respectively take1.5 hr, 3 hrs, and 2.5 hrs. Well, it’s quite a lot of driving, but even the gas costscan’t spoil your enthusiasm!
But what speed will you travel at? It’s one thing to know how far and how long it will take, but it might also be useful to know what kind of road you can expect.
For the first trip, the rate at which you’ll be driving is simply the fraction 80 mi / 1.5 hr. However, to get the actual velocity, we should divide the two numbers and find the unit rate.
Take a look at the unit rate calculator and the formula at the top. Accordingly, in order to find the unit rate, we need to input the values ofaandb. In our case, this means that for the A -> B trip, we have to input
a = 80, b = 1.5.
Don’t Miss: Spans Linear Algebra
What Is Meant By Unit Rate Formula
A unit rate is about comparing a quantity to its unit of measure and can be calculated using the unit rate formula. A unit rate that has the denominator as 1, compares a quantity to the other, which is its unit of measure. The unit rate formula to calculate the rate for any two quantities say a and b can be given as the ratio between two different quantities with different units denoted as a:b or a/b.
What Is The Difference Between Rate And Unit Rate
Rate is the ratio of two different quantities with different units, whereas unit rate expresses the number of units of the first quantity for one unit of the second quantity. In unit rate, the denominator is always of one unit. An example of unit rate is 50 miles per hour, which means 50 miles are covered in one hour, whereas, 1000 miles/10 hours, is an example of rate and not unit rate.
Don’t Miss: Beth Thomas Interview
What Is Simple Interest Rate Definition
In the context of simple interest, rate is defined as the percentage of the money that is paid by a borrower to a lender on a per annum basis. For example, if a person borrows $1000 dollars on a rate of interest of 10%, then at the end of a year, the amount to be paid back to the lender is $1100. Here, 10% is the rate of interest.
How To Find The Unit Rate
Suppose that you have two numbers, a and b. Then their rate is a / b, but what is the unit rate?
From the unit rate definition, we know that it is the equivalent fraction with denominator 1. In other words, we want to find thecwhich satisfies the equation
a / b = c / 1,
which is simply
a / b = c.
This already suggests what we must do: we dividea by b, and the result is our answer. Simple as that. A piece of cake, wouldn’t you say?
A piece of cake it might be, but let’s still see how to find the unit rate when we actually have numbers instead of symbols. The theory is fine and all, but if it’s unit rate examples that you’re looking for, then the next section is the one for you!
Read Also: My.hrw Algebra 1
How Is Rate Calculated
In general, we can write down the formula for rate as the ratio between two quantities with various units. Putting this in the ratio format, we get,
Rate = Quantity 1 / Quantity 2
For example, the steps to be followed to calculate the rate are given below.
- Step 1: Write down the two quantities that are in different units.
- Step 2: Find the ratio of quantity 1 to quantity 2.
- Step 3: Express the ratio in the simplest form to find the rate.
- Step 4: The answer will proceed with unit 1/unit 2 as the unit for the value of rate found.
Let us take an example to understand this better. Ben rode his bike for 2 hours and traveled 24 miles. To calculate the speed at which he rode, let us use the formula for rate. which is, Rate = Quantity 1 / Quantity 2. Given, quantity 1 = 24 miles, quantity 2 = 2 hours. Substituting the values in the formula, we get, Rate = 24 miles/ 2 hours. Here, the speed is the rate. So, rate = 12 miles/hour or 12 miles per hour.
Choose The Right Synonym For Rate
Verb
estimate, appraise, evaluate, value, rate, assess mean to judge something with respect to its worth or significance. estimate implies a judgment, considered or casual, that precedes or takes the place of actual measuring or counting or testing out. estimated the crowd at two hundredappraise commonly implies the fixing by an expert of the monetary worth of a thing, but it may be used of any critical judgment. having their house appraisedevaluate suggests an attempt to determine relative or intrinsic worth in terms other than monetary. evaluate a student’s workvalue equals appraise but without implying expertness of judgment. a watercolor valued by the donor at $500 rate adds to estimate the notion of placing a thing according to a scale of values. a highly rated restaurant assess implies a critical appraisal for the purpose of understanding or interpreting, or as a guide in taking action. officials are trying to assess the damage
You May Like: Michael Jackson’s Biological Kids
Rates In The Real World
Rate and unit rate are used to solve many real-world problems. Look at the following problem. Tonya works 60 hours every 3 weeks. At that rate, how many hours will she work in 12 weeks? The problem tells you that Tonya works at the rate of 60 hours every 3 weeks. To find the number of hours she will work in 12 weeks, write a ratio equal to 60/3 that has a second term of 12.
60/3 = ?/1260/3 = 240/12
Removing the units makes the calculation easier to see. However, it is important to remember the units when interpreting the new ratio.
Tonya will work 240 hours in 12 weeks.
You could also solve this problem by first finding the unit rate and multiplying it by 12.
60/3 = 20/120 × 12 = 240
When you find equal ratios, it is important to remember that if you multiply or divide one term of a ratio by a number, then you need to multiply or divide the other term by that same number.
Let’s take a look at a problem that involves unit price. A sign in a store says 3 Pens for $2.70. How much would 10 pens cost? To solve the problem, find the unit price of the pens, then multiply by 10.
$2.70 ÷ 3 pens = $0.90 per pen$0.90 × 10 pens = $9.00
Finding the cost of one unit enables you to find the cost of any number of units.
How To Find Unit Rate
The process of breaking down the cost to a smaller unit reveals the unit rate of the product. This is helpful to make informed decisions at the store, as the volumes of product in various packaging are often different. By comparing unit rates, savvy customers are able to make price comparisons based on common units of the product regardless of packaging and advertised sale prices.
Lets break down the soda cost per bottle further to determine the cost per ounce. If one 20 ounce bottle costs roughly $0.75, then dividing that cost by 20 ounces reveals the cost per ounce.
\\
As you can see, breaking down costs to the smallest unit reveals the cost savings of the sale. Of course, saving a few cents per ounce of soda may not be the deciding factor of your purchase. Other factors come into play when consumers are shopping, like brand loyalty and personal preference. However, comparing unit costs provides an objective way of making consumer choices based on the price.
The important thing to remember when analyzing unit rates is that the units must be the same. Lets consider another example to illustrate this point.
Suppose you are on a road trip in Wyoming and on the first day you covered 300 miles in 4 hours of mostly highway driving. You can quickly determine your average rate of speed as miles per hour with the following calculation:
\ \
\ \
\
\
You May Like: What Should Food Workers Do To Prevent Biological Hazards From Contaminating Food
What Is Unit Rate Formula
A unit rate that has the denominator as 1, compares a quantity to the other, which is its unit of measure. If a person runs three miles in 30 minutes, he runs at a rate of one mile every 10 minutes. The rate of miles per minute gives the distance traveled per unit of time. Unit rate is always expressed as the quantity of 1.
Let’s look into some real-time applications of unit rate.
- Time rate: Distance per unit time, average speed , and interest rates
- Cost Price: cost/pound, quantity per cost , or for comparing prices.
- Other examples can be the literacy rate, the population, and other rates which provide specific data
The unit rate formula to calculate the rate for any two quantities say a and b can be given as,
Unit Rate = Ratio between two different quantities with different units
= a:b
= a/b
Examples Of How To Find Unit Rate Or Unit Price
Ryan purchased 3 apples for $1.80. What is the unit price, or the cost of one apple?
- We want to know the price per apple unit so we set up a ratio with the number of apples in the denominator. The total price goes in the numerator. So the fraction is 1.80/3.
- Complete the division: 1.80 ÷ 3 = .60. You can conclude that the per apple price unit rate is $0.60/1. Ryan paid a unit price of $0.60 per apple .
The pottery store can make 176 coffee mugs in an 8 hour day. How many mugs can they make in one hour?
- We want to know the number of mugs made per hour unit so we set up a ratio with hours in the denominator. The total number of mugs made per day goes in the numerator. So the fraction is 176/8.
- Complete the division: 176 ÷ 8 = 22. You can conclude that the per hour mug-making unit rate is 22/1. The pottery store makes 22 mugs per hour .
Kylie can run 12 laps in 30 minutes. How many laps does she run per minute?
- We want to know the laps per minute unit so we set up a ratio with minutes in the denominator. The total laps goes in the numerator. So the fraction is 12/30.
- Complete the division: 12 ÷ 30 = 0.4. You can conclude that the per minute lap unit rate is 0.4/1. Kylie can run 0.4 laps per minute .
Recommended Reading: Reduce Definition Math
Ratios And Rates Unit Rate Definition
You know how, when you get a good grade, your parents say, “But your friend Jack got a better one. Why didn’t you?” And when you get an average grade, but it’s one of the best ones in class, you hear, “You shouldn’t look at other kids!” Funny how people can choose to compare two values only when it suits their purposes.
Mathematically speaking, this comparison is called the ratio. We often present it as a fraction, although not always. For instance, say that you got75%on the test, and the class average was 62%. Then the ratio 75 / 62 describes your score in terms of the mean. If it’s larger than 1 , then you’re above the average. If not, then perhaps it’s best to spend some more time studying?
The rate, on the other hand, tells you how much of the first number corresponds to how much of the second. This vague definition is better explained with an example.
Say that you have a dog and you give him treats every now and then. If, in a week, it eats twenty-one treats, then the corresponding rate is 21 treats per 7 days. Note how colloquially, we’d react to that with something like, “At this rate, I’ll have to buy more in a couple of days.” The word “rate” is no coincidence here.