The Concept Of The Geoid
As noted above, the actual sea-level surface of Earth, even in the absence of the effects of waves, winds, currents, and tides, is not a simple mathematical form. The unperturbed ocean surface must be an equipotential surface of the gravitational field, and because the latter reflects variations due to heterogeneities of density within Earth, so also do the equipotentials. The particular equipotential surface that coincides over the oceans with unperturbed mean sea levelconstitutes the geoid. Under the continents the geoid is not directly accessible but is rather the surface to which water would rise if narrow canals were cut through the continents from ocean to ocean. The relationships between land and ocean surfaces, ellipsoid and geoid, are shown in the figure. The local direction of gravity is normal to the geoid, and the angle between this direction and the normal to the ellipsoid is known as the deflection of the vertical.
Geoid Structure For Geographic Areas
The Standard Hierarchy of Census Geographic Entities diagram illustrates the hierarchal relationship of different geographic areas to one another. This diagram is a great tool for understanding how GEOIDs are concatenated for geographic areas that nest within other geographic areas. The table below shows the GEOID structure in TIGER/Line Shapefiles for some of the most common legal and statistical geographies, as well as example GEOIDs for different geographic areas.
Suitland, MD ZCTA
20746
* The block group code is not included in the census block GEOID code because the first digit of a census block code represents the block group code.
** ZIP Code Tabulation Areas are generalized areal representations of United States Postal Service ZIP Code service areas.
Why Do We Use Wgs 84
WGS84: Unifying a Global Ellipsoid Model with GPS The radio waves transmitted by GPS satellites and trilateration enable extremely precise Earth measurements across continents and oceans. Geodesists could create global ellipsoid models because of the enhancement of computing capabilities and GPS technology.
You May Like: Common Core Math 7 Eog Questions Geometry
Relationship To Mass Density
The surface of the geoid is higher than the reference ellipsoid wherever there is a positive gravity anomaly and lower than the reference ellipsoid wherever there is a negative gravity anomaly .
This relationship can be understood by recalling that gravity potential is defined so that it has negative values and is inversely proportional to distance from the body.So, while a mass excess will strengthen the gravity acceleration, it will decrease the gravity potential. As a consequence, the geoid’s defining equipotential surface will be found displaced away from the mass excess.Analogously, a mass deficit will weaken the gravity pull but will increase the geopotential at a given distance, causing the geoid to move towards the mass deficit.The presence of a localized inclusion in the background medium will rotate the gravity acceleration vectors slightly towards and away a denser or lighter body, respectively, causing a dimple or a bump in the equipotential surface.
The largest absolute deviation can be found in the “Indian Ocean geoid low”.
Calculating the undulation is mathematically challenging.This is why many handheld GPS receivers have built-in undulation lookup tables to determine the height above sea level.
Tom And Jerry Pair Of Satellites
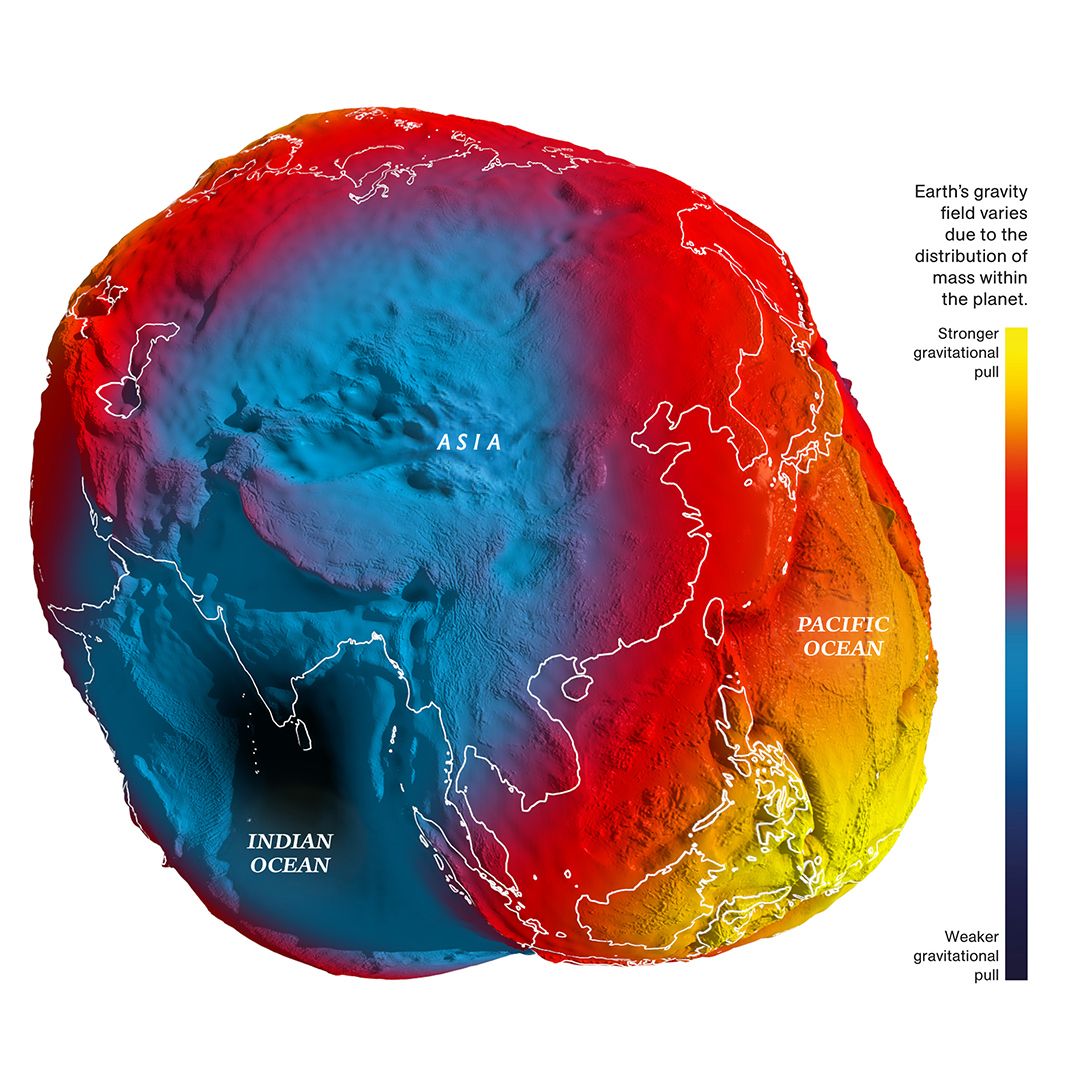
How do you measure the geoid ? If you want to measure the mean sea level, you can use a tide gauge.
Over time, you can just average out the results. And of course, that average is the mean sea level.
But youd need a lot of tide gauges placed around the entire globe. So this is why satellites like NASAs GRACE mission and ESAs GOCE mission are measuring our planets gravity field with a precision never obtained before.
How do these satellites work? GRACE is a pair of satellites in the same orbit approximately 220 kilometers apart. When the leading satellite increases speed, this means there is a greater gravitational pull. If the leading satellite slows down, this means there is less gravitational pull.
These tugs and pushes in gravity are measured using microwave pulses from one satellite to the other. Each satellite position is pinned down with GPS. The end result is the most accurate measurements of gravity anomaly to date.
Don’t Miss: What Is The Geography Of Connecticut
Why Learn About The Geoid
As gravity is one of the key elements in the field of geodesy, scientists are extracting GOCE and GRACE satellite data to study some key applications on Earth.
Geoid applications include weather forecasting, drought predictions, survey accuracy, water cycle, polar ice-mass loss, and anything that can track mass change.
Here are some detailed geoid applications:
EARTHS INTERIOR Scientists are closer than ever to earthquake prediction. Because we can retrieve variations in the geoid, these subduction events are like retrieving earthquake signatures. Geoid variations were associated with more than 98 percent of the earthquakes of magnitude 9 or above, around 60 percent for magnitude 8.8, 40 percent for magnitude 8.6, and 33 percent for magnitude 8.3.
CLIMATE CHANGE Ocean circulation, tide gauges, and sea level If all the ice melted, climate scientists would measure change by the Earths rising sea levels and tide gauges. GRACE measures mass change from the melt of Arctic ice. It helps us understand if ocean circulation is changing and how it affects world climate change.
Why Do We Require Geoid
Scientists use an irregular-shaped ball to more accurately calculate the depths of earthquakes and any other deep object beneath the earths surface, known as a geoid. Because we know the equations for those calculations on a sphere, calculations of depth and distances would be simple if Earth were a perfect sphere.
You May Like: What Is Quantitative Analysis In Chemistry
Null Methods For Obtaining Topographic Height Variability Independent Of Geoid
Detailed knowledge of the marine geoid eluded the oceanographers for a long time, and construction of its model was not an easy task due to lack of knowledge about Earths gravity field. In the absence of accurate geoid models, two null methods have been employed for obtaining the topographic height variability independent of geoid. These are collinear passes and crossover points .
Generation of time series from altimeter crossover differences involves a separate processing step to convert from height differences to a time-ordered sequence of heights referred to an arbitrary zero point . The first step is removing radial orbit error. Radial orbit error is eliminated from the reference grid by removing a quadratic trend for each pass in a simultaneous least-squares adjustment. Subsequently, crossover data are grouped into areas that are smaller relative to the horizontal scale of interest . Altimeter data obtained anywhere in the defined area can then be considered representative of the area as a whole. Each crossover difference within the area provides a measure of sea-level change between two discrete times . Once a network of crossover points is generated, the problem confines to the task of solving for a series of individual heights, which are consistent with the height differences. Least-squares techniques are usually used for computing these heights, yielding a time series of sea-level changes at any given grid point from the first altimeter pass to the last.
Modeling The 2004 Sumatra Earthquake
The coseismic geoid and gravity anomalies from the 2004 Sumatra earthquake are obtained from a new, compressible self-gravitating Earth model that is fully realistic as it builds on PREM and represents the elastic limit of viscoelastic models, recently used for PGR studies and developed for coseismic studies by Smylie and Manshina and Sun and Okubo . This approach differs from that followed by Gross and Chao and de Linage et al. , both using compressible models based on a free oscillation scheme. The gravitational part of the phenomenon is dealt with self-consistently and the effects of compressibility are taken into account both in the initial state and during the perturbations , on the basis of the RungeKutta integration in the radial variable of the differential equations describing momentum conservation and self-gravitation. Because the gravitational effect of sea-level feedback has been important for the 2004 Sumatra earthquake , a self-consistent treatment of the global ocean layer of PREM is included. In this way, the approaches used by Han et al. and de Linage et al. are refined in the results shown in this section although, from a quantitative point of view, the approach used in the present analysis does not significantly change the results presented by these authors.
Figure 61. Coseismic geoid anomalies for compressible S-PREM and O-PREM, after the 350 km Gaussian filtering.
Journal of Geophysical ResearchJournal of Geophysical Research
T. Lay, in, 2015
Recommended Reading: What Is Average In Math
Why Is The Geoid Not A Perfect Sphere
There are many reasons why the geoid isn’t a sphere. First and foremost, the Earth itself isn’t a sphere. It is closer to an ellipsoid, being flattened at the poles by the centrifugal force of its own rotation. … That mass distribution affects the gravitational field and makes the geoid asymmetrical too.
What Is The Process Of Creating A Geoid
The geoid is caused by gravity anomalies, which occur when the earths gravity field differs due to variations in the mass distribution. Theyll only see features that are relatively large . The shape of the geoid is extremely complex.
The ellipsoid, on the other hand, is a simple shape created by rotating an elllipse.
You May Like: What Does Msw Stand For In Psychology
The Geoid Equation: Analytic Results For The Stokes Coefficients Of Degree 2 And Order 1
Since the classical geoid is defined in terms of sea level, it should be clear that, notwithstanding the approximations upon which the SLE is based, it must provide the basis for a prediction of its time dependence. If the geoid is to be observed from space, it is also clear that the sea level that it represents will be measured not with respect to the surface of the solid Earth but rather with respect to the planet’s center of mass relative to which the orbit of an Earth satellite is represented. This shift of the datum with respect to which the evolving sea level is measured is easily accommodated in the SLE formalism. Using this apparatus, we may define the spacetime evolution of the quasistatically evolving geoid as
The issue as to whether the space-independent but time-dependent conservation of mass factor, /g, which is clearly required in the SLE, should also appear in the geoid eqn is an issue that was raised in Chambers et al. in connection with the use of the equation to compare GIA predictions of the time-dependent geoid with the GRACE satellite observations, and so, this term has been placed in brackets in eqn . The term is of course required in the description of the true sea level-related geoid as discussed in detail in Peltier et al. .
Figure 35 shows examples of the global fields S
Dr.Antony Joseph, in, 2014
Geoids In Downloads From Datacensusgov
Data downloaded from data.census.gov containstwo fields of GEOID information, GEO.id and Name. The table below shows thefields as they appear in a file downloaded from the data.census.gov searchresults page. The first row in the table contains data field names. The secondrow contains table descriptions. Rows 3-5 contain GEOID information for threecounties in the state of Delaware.
You May Like: What Is Fixation In Psychology
Determination Of The Geoid Surface
There are many mathematical methods that help to determine and calculate the surface of the geoid. The undulations, i.e. the smooth up and down movement of the geoid surface, are calculated by various approaches combined together. Calculation of the undulating surface is challenging mathematically. Hence, because of this many of the GPS receivers that are handheld have built-in undulation lookup tables which are helpful in determining the height above sea level. The stokesian approach is the one that is widely used for the calculation of undulating surfaces. The precise solution of the geoid given by Vanicek and co-workers improved on the Stokesian approach for the computation. The solution obtained as such enables the accuracy to be in the range of millimetre-to-centimetre which is an order-of-magnitude better than the previous classical situations.
Many of the calculations of the undulations of the geoid surface use approaches such as least-squares collocation, fuzzy logic, artificial neural networks, radial basis functions, and geostatistical techniques to estimate the uncertainties displayed in the undulations of the geoid. Out of all of them, the geostatistical approach has been defined as the most improved technique while utilizing for the prediction of the geoid undulation.
Dig A Canal Away From The Ocean
The geoid is a measurement of mean sea level . When you average out the motion of waves, the level at which water settles is MSL.
If you want to calculate MSL, all you have to do is just measure the average level of the oceans and there you have it.
But what about the land?
Lets say you dig a canal away from the ocean inwards to the land. The level the water would settle could be interpreted as the mean sea level.
The geoid is the hypothetical MSL without digging a canal And surveyors use it to measure precise surface elevations as a true zero surface in a vertical datum.
Recommended Reading: How To Figure Out Math
What Is A Geoid Why Do We Use It And Where Does Its Shape Come From
A geoid is the irregular-shaped ball that scientists use to more accurately calculate depths of earthquakes, or any other deep object beneath the earths surface. Currently, we use the WGS84 version .
If Earth were a perfect sphere, calculations of depth and distances would be easy because we know the equations for those calculations on a sphere. However, the Earth more closely approximates an ellipsoid, which is what a ball looks like if you sit on it. Ellipsoid calculations arent as easy as spherical calculations, but theyre still well-known and do-able. Be that as it may, we all know that the earth is not really an ellipsoid because there are oceans, and mountains, and valleys, and many other features that are not part of an ellipsoid.
The geoid is an imaginary sea level surface that undulates over all of the earth it isnt just for the oceanic areas, it also extends through the land masses.
You can generalize the relationship between the ellipsoid, the geoid, and the actual shape of the earth with this:
geoid + ellipsoid = Earth
Gravity Anomalies And Dynamic Topography
If both geoid and dynamic topography are correlated with density anomalies, it should be possible to use the geoid as a proxy for dynamic topography. We note that the geoid is equivalent to gravity anomalies, as they can be described by the same spherical harmonic coefficients, so whatever is written here regarding the geoid can be equivalently formulated with respect to free-air gravity.
Figure 5. Correlation and ratio of residual geoid and topography as a function of spherical harmonic degree. Residual topography beneath water is divided by 3.3/2.27 = 1.45 . High correlation for higher degrees in part results as a consequence of corresponding corrections applied to both geoid and topography, which increases correlation regardless of whether the correction is appropriate or not. If the geoid is uncorrected, correlation still tends to be higher for degrees 1331 than 112 the ratio is reduced to 0.7% for degrees 1931.
A geoidtopography ratio
Mehdi Eshagh, in, 2021
You May Like: What Is Abiotic Factors In Biology
Geoid Ellipsoid And Gravity Field
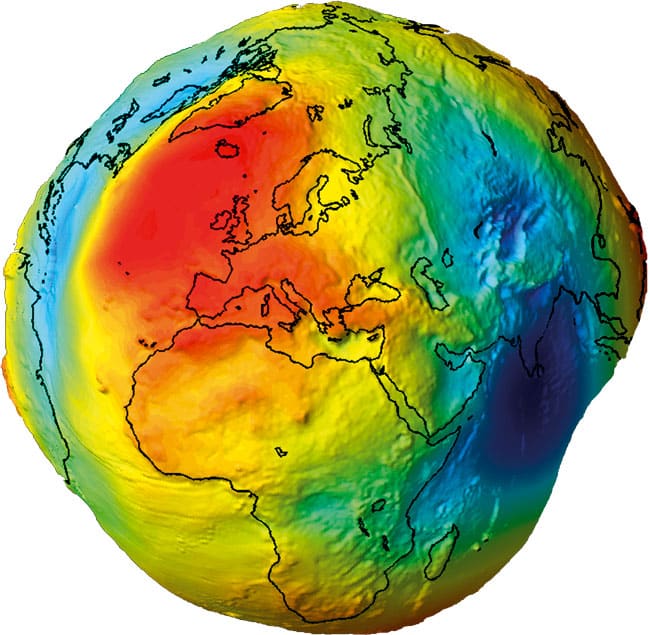
Figure 1. Gravity field anomalies from GRACE. Courtesy NASA.
To calculate the shape of the geoid, the gravity field of the Earth must be calculated along with both its internal and external gravity potential. A particle on the surface of the Earth is acted on by two forces, the gravitational force represented by
The source of gravitation in the above equation is the mass density field which is multiplied by the coupling constant g of the inertial and gravitational forces. There are many solutions to this field equation that effectively define the gravitational potential.
The reference ellipsoid is usually chosen to be the same volume as the geoid and is described by its semi-major axis defined by the equatorial radius and the flattening that makes it appear oblate. The quantity f=/a, where b is the semi-minor axis , is a purely geometrical relationship. The mechanical ellipticity of the Earth which is the dynamical flattening caused by its rotation has been determined to a high degree of precision by observation of satellite orbit perturbations. Its relationship with the geometric flattening is indirect and depends on the internal density distribution of mass in the Earth. The 1980 Geodetic Reference System posited a 6 378 137 m semi-major axis and a 1:298.257 flattening. This system was adopted at the XVII General Assembly of the International Union of Geodesy and Geophysics and formed the basis for geodetic positioning by the Global Positioning System.
Us Department Of Education And State
The US Department of Education is responsible for issuing and maintaining geographic codes for elementary, secondary and unified school districts throughout the nation. Also, individual states use state-defined standards to establish geographic codes for voting districts and state legislative upper and lower districts. Voting districts nest within counties and consequently, voting district GEOIDs contain both state and county FIPS codes. Similarly, state FIPS codes comprise a portion of school district and state legislative district GEOIDs, as they share a nesting relationship within states.
Recommended Reading: What Is The Unit For Acceleration In Physics
Geoids: The Uglier Truth About Our Planet
Complicating things further, the earths surface is not actually smooth like these idealized ellipsoidal models. Because the density of the planet is inconsistent, gravitational forces pull in or push out the earths surface in different places, resulting in a planet that looks more like a lumpy potato than an egg.
Models that approximate the lumpy potato we call home are called geoids. The surface of a geoid represents a Mean Sea Level , or a conjecture of the oceans surface if tides, winds, and other factors that affect its movements didnt exist. The only factor that affects the MSLs shape is the earths gravity field.
Unlike ellipsoidal models, geoid models are locally basedor, at least, more local than the entire surface of the Earth. For instance, surveyors in the United States currently use the North American Vertical Datum of 1988 .
That is, they will for the next couple of years. The National Geodetic Society is set to replace the NAVD88 in 2022 with a newer model derived using GPS rather than the physical survey marks used by the current model.