Parallelogram Law Of Vector Addition
If we were to represent two vectors magnitude and direction by two adjacent sides of a parallelogram. The resultant can then be represented in magnitude and direction by the diagonal. This diagonal is the one which passes through the point of intersection of these two sides.
Power is work done in unit time .
How Do You Prove The Area Of The Circle
If a circle is folded into a triangle, the radius becomes the height of the triangle and the perimeter becomes its base which is 2 ×× r. We know that the area of the triangle is found by multiplying its base and height and then dividing by 2, which is: ½× 2 ×× r × r. Therefore, the area of the circle is r2.
Area Of An Equilateral Triangle
To find the area of an equilateral triangle, we can use the following formula:
The area of an equilateral triangle is equal to
where s is the length of any side of the triangle
What is the formula for the area of an equilateral triangle given the length of its side?Given side of length s, the area of an equilateral triangle is s-squared times the square root of three over four.
Also Check: Chapter 4 Test Form 2c
What Is The Surface Area Of A Cylinder
The surface area of a cylinder is the total region covered by the surface of the cylindrical shape. The total surface area of a cylinder is given as the sum of lateral surface area and the area of two bases. It is mathematically expressed as 2r and is expressed in square units, like m2, in2, cm2, yd2, etc. The curved or the lateral surface area of a cylinder is calculated with the formula, Curved surface area = 2rh.
Surface Area Of A Square Pyramid
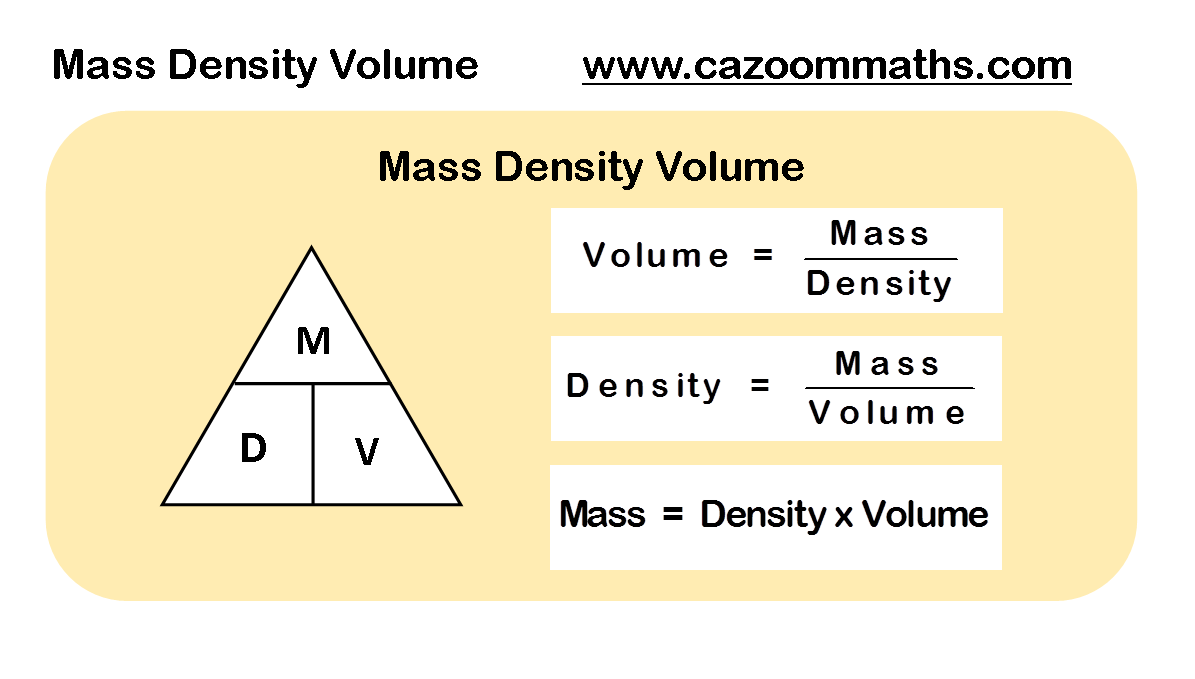
Recommended Reading: Does Kamala Harris Have Children
Satelite Motion Orbital Speed Period And Radius
| Formula | |
|---|---|
| v = \sqrt } | v is the orbital speed of the satellite G is the universal gravitational constantM is the mass of the attracting body r is the distance from the center of mass M to the position of the satellite |
| T = \sqrt } | T is the orbital period of the satelliteG is the universal gravitational constantm is the mass r is the distance from the center of mass M to the the position of the satellite |
| v = \dfrac | v is the orbital speed of the satellite r is the distance from the center of mass M to the the position of the satellite T is the orbital period of the satellite |
Kinetic Theory Of Gases
Based on the primary assumptions that the volume of atoms or molecules is negligible, compared to the container volume and the attractive forces between molecules are negligible, the kinetic theory describes the properties of ideal gases. Here are the most important physics formulas related to the kinetic theory of monatomic gases.
Pressure = 1/3
Here, P is pressure, N is the number of molecules and v2 is the mean squared particle velocity.
Internal Energy = 3/2
Don’t Miss: Define Variability In Math
Area Of Polygons With Coordinates
A method for finding the area of any polygon when the coordinates of its vertices are known is given as below. But first, you have to number the vertices in order, going either clockwise or counter-clockwise, starting at any vertex.
The area is then given by the formula
\}}\bigg|\)
Where \ is the \ coordinate of the vertex \, \ is the \ coordinate of the vertex \
Check out this article on Circle here.
A Comprehensive List Of All The Physics Formulas
Learning physics is all about applying concepts to solve problems. This article provides a comprehensive physics formulas list, that will act as a ready reference, when you are solving physics problems. You can even use this list, for a quick revision before an exam.
Like it? Share it!
Learning physics is all about applying concepts to solve problems. This article provides a comprehensive physics formulas list, that will act as a ready reference, when you are solving physics problems. You can even use this list, for a quick revision before an exam.
Physics is the most fundamental of all sciences. It is also one of the toughest sciences to master. Learning physics is basically studying the fundamental laws that govern our universe. I would say that there is a lot more to ascertain than just remember and mug up the physics formulas. Try to understand what a formula says and means, and what physical relation it expounds. If you understand the physical concepts underlying those formulas, deriving them or remembering them is easy. This ScienceStruck article lists some physics formulas that you would need in solving basic physics problems.
You May Like: Kuta Software Infinite Geometry The Segment Addition Postulate Answer Key
Area Of Trapezoid / Trapezium
A trapezoid or trapezium is a 4-sided polygon that has at least one pair of parallel side.It is called a trapezoid in North America and a trapezium in Britain and other countries.
Area of trapezium = × × height
How to find the area of a trapezoid?Remember to use the height that is perpendicular to the base.
Why Is The Formula For The Surface Area Of A Circle Not ^2
- 182
- 0
- 17
No, why would you think that? The explanation is simple: that’s simply not the correct area for the surface area of a circle.
NascentOxygen said:Where did you learn of that method? Does it work for any geometric shape, do you know?
nickadams said:yes it works with many shapes for area, surface area, and volume. Like for the area of a rectangle you could take a line that is the length between opposite edges longways and lay it side by side number of times and then multiplying the units together gives you the appropriate units^2 of area.
So in order to keep this approach for circles I would have to find the area of triangles made up of two radiuses set a certain angle apart and with the arc length subtending that angle as the third side. Then I could multiply these triangles by and get the area of the circle…
radiusangle0.5angle
HallsofIvy said:By the way, am I the only one wondering why nickadams keeps saying “surface area of a circle” when he clearly means “surface are of a sphere“?
Recommended Reading: Elton John Kids Adopted
How To Calculate Area
Let us see how to calculate the area of a shape with the help of a grid. The area of any shape is the number of unit squares that can fit into it. The grid is made up of many squares of sides 1 unit by 1 unit. The area of each of these squares is 1 square unit. Hence, each square is known as a unit square. Look at the figure shown below. Let us find the area of the shape drawn in the grid.
The area of this shape is the number of shaded unit squares.
Thus, the area of the shape = 9 square units. Now, let us look at another example. When the shape does not occupy a complete unit square, we can approximate and find its value. If it occupies about 1/2 of the unit square, we can combine two such halves to form an area of 1 square unit. Observe the figure given below.
Here, the area occupied by the shape = 4 full squares and 8 half squares. Together this forms an area of 8 square units. If the shaded region is less than 1/2, we can omit those parts. For regular shapes, we have certain formulas to calculate their area. Note that this is only an approximate value.
Example Of Calculating Volume And Surface Area

To find surface areas of objects with a curved surface, such as a sphere, there is no choice but to memorize the volume and surface area formulas. But for other objects, we can often break them down into other recognizable polygons and shapes whose volume or surface area we can easily find. For example, with a pyramid, you simply calculate the surface area of the base and add that to the surface area of each triangular side.
Let’s find both the surface area and the volume of a square pyramid with a base length of 6 inches and a slant height of 5 inches.
Read Also: Unit Test Edgenuity Algebra 2
Definition Of Length Area Volume
Length area and volume, Dimensional measures of one-dimensional, two- dimensional, and three-dimensional geometric objects. All three are magnitudes, that represent the size of an object. We can define length as the size of a line segment , the area is the size of a closed region in a plane, and volume is the size of a solid.
Formulas for the area as well as the volume are based on lengths. For example, the area of a circle equals times the square of the length of its radius , and the volume of a rectangular box is the product of its three linear dimensions that is: length, width, as well as height.
In this article, we are going to discuss length area and volume, volume with fractional edge lengths and unit cubes, differential length area and volume as well as measuring volume as area times length.
Approximate Area By Counting Squares
Sometimes the squares don’t match the shape exactly, but we can get an “approximate” answer.
One way is:
- more than half a square counts as 1
- less than half a square counts as 0
Like this:
This pentagon has an area of approximately 17
Or we can count one square when the areas seem to add up.
Example: Here the area marked “4” seems equal to about 1 whole square :
This circle has an area of approximately 14
But using a formula is best:
Read Also: Open Sentence Definition Math
Perimeter Area And Volume
1. The perimeter of a polygon is the distance around the outside.
2. The area of a simple, closed, planar curve is the amount of space inside.
3. The volume of a solid 3 shape is the amount of space displaced by it.
Some formulas for common -dimensional plane figures and 3 -dimensional solids are given below. The answers have one, two, or three dimensions perimeter is measured in linear units , area is measured in square units , and volume is measured in cubic units .
| Table | |
| is the length of the side of the square. | |
| Rectangle | are the lengths of the rectangle’s sides . |
| Triangle | |
| are the lengths of the two legs of the triangle | |
| Circle |
| is the length of the side of the square. | |
| Rectangle | are the lengths of the rectangle’s sides . |
| Triangle | are the base and height |
| Triangle | are the side lengths and s |
| is the length of the base and h | |
| are the lengths of the parallel sides and h the distance between the parallels. | |
| Circle |
| is the length of the side. |
| Right Rectangular Prism |
| is the area of the base, h |
| is the area of the base, h |
What Is The Formula For Surface Area
The formula to find the surface areas of different geometrical shapes is to add the areas of each of their faces. It can be very tedious to find the area of each face individually, so we have surface area formulas for each of the geometrical figures. Some of the formulas are listed below:
- Total surface area of a cube = 6 × 2
- Surface area of sphere = 4r2
- Total surface area of cone = r
You May Like: Linear Algebra Span Definition
Physical Formulas For Quantities In Relativistic Dynamics
All the known quantities in classical mechanics get modified, when we switch over to relativistic mechanics which is based on the special theory of relativity. Here are formulas of quantities in relativistic dynamics.
Relativistic momentum p = m0v where m0 is the rest mass of the particle.
Rest mass energy E = m0c2
Total Energy E = )
Surface Area Of Prism
A prism is a 3D solid object made up of two congruent bases which are polygons and congruent lateral faces which are rectangular in shape. There are two types of areas that a prism has – the lateral surface area and the total surface area. The lateral area of a prism is the sum of the areas of all its lateral faces whereas the total surface area of a prism is the sum of its lateral area and area of its bases.
The lateral surface area of prism = base perimeter × height
The total surface area of a prism = Lateral surface area of prism + area of the two bases = + Lateral surface area = + .
There are seven types of prisms based on the shape of the bases of prisms. The bases of different types of prisms are different so are the formulas to determine the surface area of the prism. Observe the table given below to understand this concept behind the surface area of various prisms:
| Shape | Surface Area of Prism = + |
|---|---|
| Triangular Prism | Surface area of triangular prism = bh + H |
| Square Prism | |
| Surface area of trapezoidal prism = h + l | |
| Pentagonal Prism | |
| Surface area of octagonal prism = 4a2 + 8aH |
Related Articles
Don’t Miss: Theory Of Everything 2 Soundtrack
Frequently Asked Questions On Physics Formulas
1. Where can I find all the formulas of Physics?
You can discover all major and commonly used physics formulas from the above list provided over here and whenever you need them, you can use them for free within no time.
2. What are the major formulas in physics?
Basic Formulas in Physics are provided below for the sake of students. So, let us have a loot at them before solving the physics problems:
- v=u+at
- P=force/area
3. How Can I learn Scientific Formulas?
One of the finest ways to understand and learn the physics formulas is practicing & memorizing the derivation of the formula. Solve the example sums with the formula and read the formulas fluently in a day. Use the memory palace and jot down all the formulas in an understandable way and memorize them easily.
4. How to Memorize Physics Formulas?
There are four three steps you should follow to memorize all physics formulas. They are as under
5. What are the tips to learn Physics Formulas?
Below are furnished top tips to quickly learn several Physics formulas:
- Practice concentration
List Of Physics Formulas & Equations
Physics is the most basic subject of all sciences, and also it seems very harder to master. Basically learning physics is nothing but studying the basic laws which lead our universe. One can master in physics if they understand the theories thoroughly, and also they can easily identify the relation between the quantities or numbers by which they can form the formulas, derive it and learn simply.
Students who are looking for physics formulas can grab the list from this page and utilize them to revise daily and before your exams. While memorizing the physics formulas, first of all, try to understand what a formula says and means, and then what physics relation it outlined. If you comprehend the physics topics underlying those formulas, deriving & memorize them will be easy for you. So, use the list of physics equations available over here and solve the basic physics problems very easily & quickly.
Recommended Reading: Similar Math Definition
Momentum And Energy Transformations In Relativistic Mechanics
Consider the same two frames as in case of Lorentz coordinate transformations above. S is moving at a velocity v along the x-axis. Here again is the Lorentz factor. In S frame and in S frame are momentum components. Now we consider formulas for momentum and energy transformations for a particle, between these two reference frames in relativistic regime.