The Formula For Tension In A Rope Pulling Blocks Horizontally
This is the most common form of tension in a string problem. A rope is used to pull two blocks separated by a distance. There can be n number of blocks, but the tension in each rope will be different. Here, a force F is pulling blocks with mass M1 and M2 across a frictionless surface.
For the entire system: Fnet = Total mass*acceleration => Acceleration = F/
Using the free body diagram as shown above we focused on the two blocks separately and calculated the formula for tension.
T = M1*a T = F + M2*a
Both equations can be used to find the value of tension in the rope. The values of tension will be the same. The SI unit of tension force is Newton. You can read our blog post on units of force for more details.
Facts About Tension Force
How To Calculate Tension In A String: Exhaustive Insights
Before going to calculate the tension in the string, let us discuss what is meant by tension?
Tension is a contact force that transfers by means of string or cable or, similar objects. Tension always acts away from the body along the string.
In this article, we are going to calculate the tension acting on the string.
Read Also: Prentice Hall Gold Algebra 1 Teaching Resources Answers Chapter 9
Example : Weight On An Incline A Two
Consider the skier on a slope shown in Figure 2. Her mass including equipment is 60.0 kg. What is her acceleration if friction is negligible? What is her acceleration if friction is known to be 45.0 N?
Figure 2.Nfw ww|| Nwfw||
Strategy
Solution
The magnitude of the component of the weight parallel to the slope is\boldsymbol =w\:\textbf\:=mg\:\textbf\:},and the magnitude of the component of the weight perpendicular to the slope is\boldsymbol=w\:\textbf\:=mg\:\textbf\:}.
Neglecting friction. Since the acceleration is parallel to the slope, we need only consider forces parallel to the slope. The forces parallel to the slope are the amount of the skiers weight parallel to the slope\boldsymbol}and friction\boldsymbol.Using Newtons second law, with subscripts to denote quantities parallel to the slope,
where\boldsymbol\parallel}=w_ =mg\:\textbf\:},assuming no friction for this part, so that
is the acceleration.
Including friction. We now have a given value for friction, and we know its direction is parallel to the slope and it opposes motion between surfaces in contact. So the net external force is now
and substituting this into Newtons second law,\boldsymbol =\frac}},}gives
We substitute known values to obtain
which yields
which is the acceleration parallel to the incline when there is 45.0 N of opposing friction.
Discussion
Tension Formula: Overview Facts & Examples
We have all been to parks and recreational centres. Often there are a lot of swings for us to enjoy. We can sit on the seat, and swing ourselves back and forth and enjoy a smooth breeze. The swings are operational due to the Tension Force. The tension formula can be represented as \.
Tension occurs due to the direction of pull on the object and along the length of the given rope. Furthermore, it is important to note that Newton is the SI unit of Tension. In this article, we will discuss about tension formula in detail. Scroll down to find more about Tension and its formula!
Recommended Reading: Geometry Dash Hacks No Survey
Tension String Forces Problems With Solutions
Several problems with solutions and detailed explanations on systems with strings, pulleys and inclined planes are presented. Free body diagrams of forces, forces expressed by their components and Newton’s laws are used to solve these problems. Problems involving forces of friction and tension of strings and ropes are also included.
Write The Equation Of Forces In A Pulley
The forces acting on the pulley due to the object of mass M1 is
The force due to gravity is applied in the negative y-direction hence we have taken it as negative and the tension is exerted in the upward direction in the positive y-direction. The acceleration of the mass is also in the downward direction.
The forces acting on the pulley due to the object of mass M2 is
The acceleration of both the masses on the pulley will be at the same rate but only the direction of motion differs.
Also Check: Explain Why There Are Different Branches Of Chemistry
How To Calculate Tension In Circular Motion
When the string is subjected under tension in circular motion, tension force will always act towards the center of the circle. Tension force is approximately equal to the centripetal force,
T ~ mv2 / R
This above condition is satisfied only when the object moves in circular motion.. If the object suspended moves fast enough then two components TX and TYis incorporated. Using the formula, T = 1/2, the tension is calculated. The component TX provides centripetal force and so Tx = mv2 . The component TY corresponds to weight of the object, i.e. TY = mg . The component TY depends on the speed of the object moving in circular motion.
If the object moves at a faster rate of speed tension is gives as, TY = Tx . If the object moves at a lower rate of speed then tension is calculated as T= .
The Formula For Tension In A Rope Attached To A Weight At An Angle
Tensionforce is developed in a rope when a weight is attached to it. The tension developed in the rope should be equal to the gravitational pull on the weight. But this is true only for a case when the rope is vertically suspended. The formula for tension also depends on the angle of suspension. Here in this article, we look at the examples, formulas, and numerical problems for tension when the rope is suspended at an angle to the ceiling.
The weight of mass m is suspended by two ropes with tension T1 and T2. The tension in both the ropes will be different, so we have to derive two separate sets of the formula for tensions in both strings. Since the weight is static, the net forces acting on the weight in the x and y direction should be zero.
We will start by drawing a free-body diagram and resolve the forces in x and y directions.
Resolving the forces in y-direction: The forces acting in the y-direction are a downward gravitational pull and component of tension forces T1 and T2 in an upward direction. Equating the force we get:
T1 sin + T2 sin = m*g –
Resolving the forces in x-direction: The forces acting in the x-direction are the components of tension forces T1 and T2 in opposite directions. Equating the forces we get:
T1cos = T2cos
Solving equations and , we get the formula for tension.
T1 = /cos]
T2 = /cos]
Recommended Reading: Example Of Span Linear Algebra
Tension Formula: Concepts Definition And Solved Examples
Forces are given many names which are like push, pull, thrust, lift, weight, friction, and tension. The student will learn one particular kind of force which is tension with tension formula. The word tension comes from a Latin word meaning to stretch.
You should realize that tension is really a get the connector. The strain pressure pulls outward across the two ends from the string. This Tension within the rope must comparable to the load from the supported mass, which may be easily demonstrated using Newtons second law. Here, the only real exterior forces functioning on the mass is going to be the weight W and also the tension T provided through the rope. Thus,
Forces are given many names which are like push, pull, thrust, lift, weight, friction, and tension. Traditionally, we may group these forces into several categories and given names relating to their source, like how they are transmitted, or their effects. The most important of these categories will be discussed in this section with some interesting applications. Further examples of forces will also be discussed. The student will learn one particular kind of force which is tension with tension formula. The word tension comes from a Latin word meaning to stretch. Let us learn it!
In What Cases Would The Force Of Tension Between Two Bodies Connected By The Same Rope Differ
The rope acts as a transferring agent of the force, so there should never be a scenario in which two objects connected by one rope experience tension forces of different magnitudes.
Stay tuned to BYJUS and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Read Also: Molecular Geometry Ccl4
How To Calculate Tension Force In Physics
Lifting a Mass. Though a straightforward application of Newtons second law, many find this problem deceptive. The common misconception which is carried into it is that the tension in the rope must equal the weight of the hanging object. When the mass is accelerated, that is not so. You may change the data and then click on either tension or acceleration in the equation below to calculate its value.
For a mass m= kg, the rope must support its weight = mg =Newtons to hold it up at rest. If the acceleration is a=m/s2 then a net force=Newtons is required to accelerate the mass. This requires a tension of T=Newtons. Note that the tension is equal to the weight only if the acceleration is zero, and that if the acceleration is negative , the tension is less than the weight. If you enter a downward acceleration greater than 9. 8 m/s2 you will get a negative tension, showing that you must force it downward to get an acceleration greater than that of free fall.
Video advice: Introduction to tension
An introduction to tension. Solving for the tension in a set of wires when a weight is hanging from them. Created by Sal Khan.
Double Trouble In 2 Dimensions
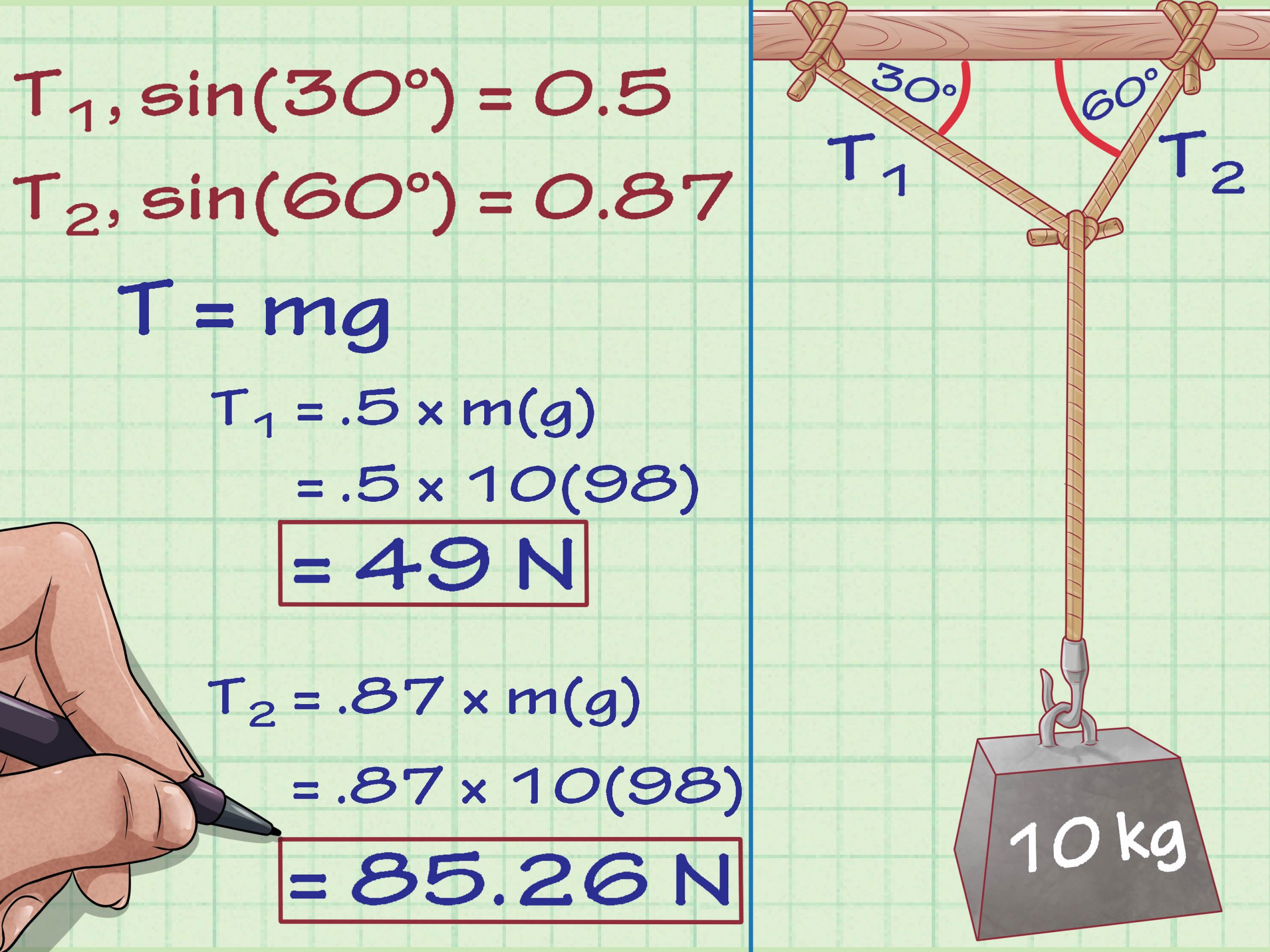
In the Newtons laws unit, the topic of two-body problems was introduced. A pair of problem-solving strategies were discussed and applied to solve three example problems. Such two-body problems typically involve solving for the acceleration of the objects and the force that is acting between the objects. One strategy for solving two-body problems involves the use of a system analysis to determine the acceleration combined with an individual object analysis to determine the force transmitted between the objects. The second strategy involved the use of two individual object analyses in order to develop a system of two equations for solving for the two unknown quantities. If necessary, take the time to review the page on solving two-body problems. This page will build upon the lessons learned earlier in the Newtons Laws unit.
Video advice: Tension Force Physics Problems
This physics video tutorial explains how to solve tension force problems. It explains how to calculate the tension force in a rope for a object descending with a downward acceleration using newtons laws of motion. it also discusses how to use free body diagrams and the weight force to calculate the tension force in two ropes at different angles. Theres another tension force physics problem that asks you to calculate the tension in two cables / ropes where one rope is in the horizontal direction and the second rope is at an angle.
Recommended Reading: How To Do Percent Error Chemistry
Dimensional Formula Of Tension
Tension is a type of force that acts along the length of the medium such as rope or string. A force is necessary to put these objects under tension. Tension is also named something exciting, i.e. action-reaction pair.
The Tension Dimensional Formula =
Tension is nothing, but its a force that has got another improved name. Tension acts at both the end of the string . The tension force is available on each point of the string.
Qhow To Find Tension In A Pulley System
In a pulley system the total force equals the tension in the rope and the gravity force pulling at the load.
A pulley is a rotating wheel having curved rim which is connected to a rope, string or a cable. It simply reduces the energy and the power required to lift heavy objects. The tension force in such case is calculated using the formula T = M x A .
Read Also: How To Calculate A Half Life
Common Misconceptions: Normal Force Vs Newton
In this section we have introduced the quantity normal force, which is represented by the variable\textbf.This should not be confused with the symbol for the newton, which is also represented by the letter N. These symbols are particularly important to distinguish because the units of a normal force happen to be newtons . For example, the normal force\textbfthat the floor exerts on a chair might be\boldsymbol=100\textbf}.One important difference is that normal force is a vector, while the newton is simply a unit. Be careful not to confuse these letters in your calculations! You will encounter more similarities among variables and units as you proceed in physics. Another example of this is the quantity work and the unit watts .
Faqs On Tension Formula
Q.1. What is the Tension force?Ans: The pulling force exerted axially by a rope or cable along its length is known as Tension force.
Q.2. Is tension a contact or a non-contact force?Ans: Tension acts in a rope when the surface is in direct contact with the rope. Thus, it is a contact force.
Q.3. Does gravity affect the tension force?Ans: Tension force is due to the electromagnetic forces developed in the rope when it is taut. It is independent of gravity. The rope under tension pulls the objects connected it its two ends. The magnitude of the tension depends on the force with which the objects connected to it are pulling. Therefore, if the force exerted by the objects is due to gravity, tension force indirectly depends on gravity. In other situations, it is independent of gravity.
Q.4. What is the SI unit of tension?Ans: The SI unit of Tension is Newton.
Q.5. Suppose two blocks of mass \ each are suspended by a string. What will be the tension force in the string? Take \.Ans: Tension will balance the weight of the two masses.The weight of the two blocks, \Thus, the tension in the rope, \.
Q.6. What is the formula for tension?Ans: The formula for tension is \.
We hope this detailed article on Tension Formula helps you in your preparation. If you get stuck do let us know in the comments section below and we will get back to you at the earliest.
Read Also: Kim Kardashian’s Biological Father
How To Calculate Tension
Understanding tension definition, force could be a key to understand however, ropes and cables expeditiously transfer force over a big distance. Knowing how to calculate tension is vital, not only for physics students but also for engineers and designers.
A sledge pulled by a team of Siberian Huskies could be an excellent example to validate this truth. Behind using the normal force, the ropes attached to the sledge, passes the force from running huskies to the sledge. Tension is a type of force on the length of a medium, particularly a force carried by a versatile medium, like a rope or cable. Tensions are often outlined as associate degree action-reaction types of forces.
To construct safe buildings, Most Engineers assume that strain on an object will be resisted by the strain due to the objects weight before yielding. Anything stretched or hung, supported or swung from a rope is subject to the force of tension. Like all forces, tension will accelerate objects or cause them to deform.
This article will stress the tension definition, its formula and calculate it effectively in different practical situations. Moreover, it will also give examples of its practical implications.
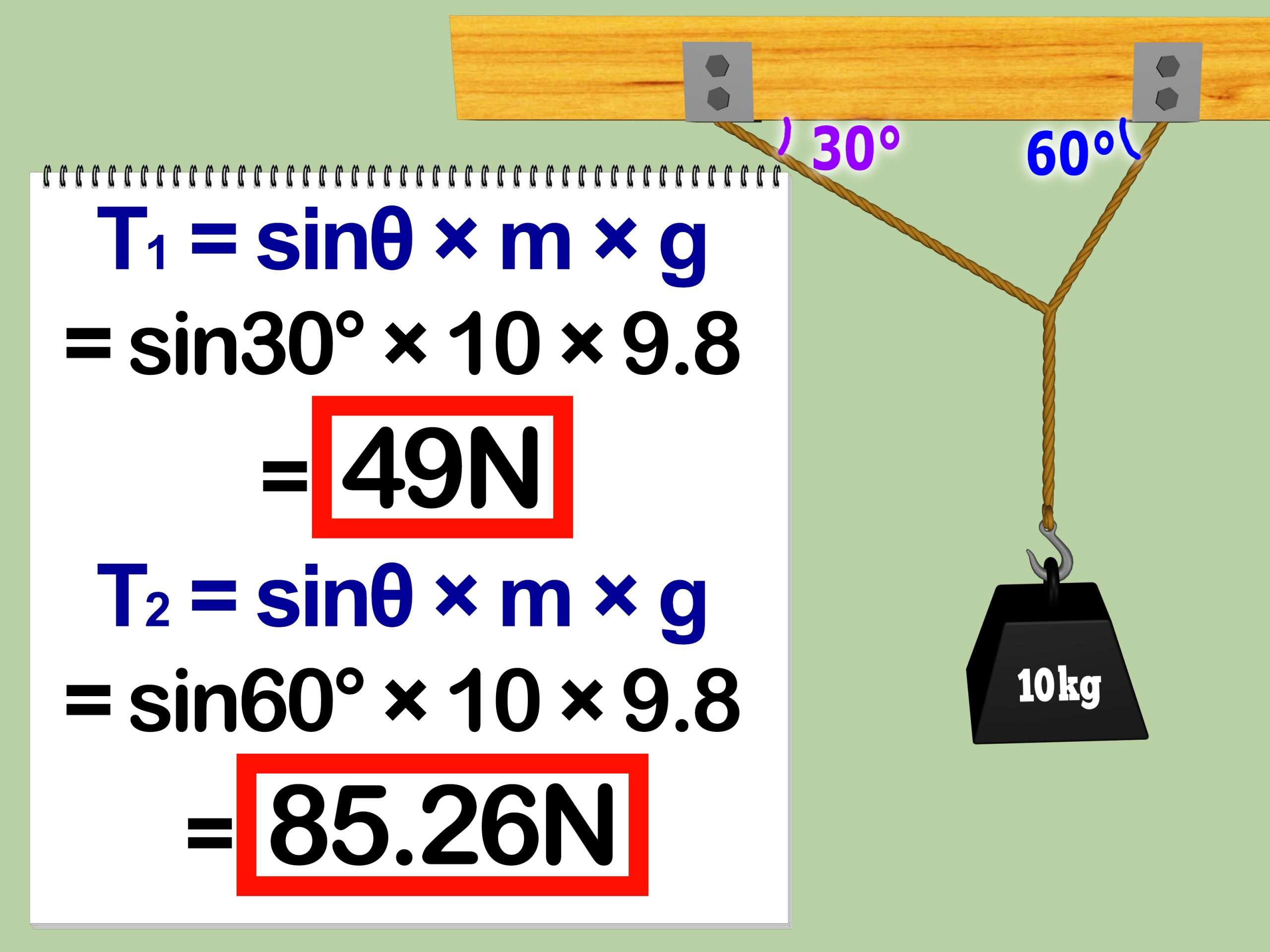
Qwhat Is Tension At An Angle In A String
Tension is the force transmitted between a string or a cable or a rope and the weight suspended.
A weight is suspended by two strings T1 and T2 from a rigid support. Tension force is different in both the strings. Weight suspended will be static since the net force acting is zero due to the equal and opposite forces action upon the weight.
Firstly we need to resolve the factors in y-direction. Gravitational force acts downwards and tesnional force acts upwards in both the strings. On equating the forces we get:
T1sin + T2sin=mg
Resolving forces in x-direction and on equating those forces we get:
T1cos = T2cos
On equating and , T1 and T2 is:
T1 = T2 T2 = T1
From above equations we infer that greater the angle of suspension greater will be the tension force present in the system. 90 degree is the maximum angle at which the maximum tension occurs.
Read Also: Glencoe Geometry Practice Workbook Answers