How To Use Foil Math

Multiplying Binomialsusing The Foil Method

Multiplying polynomials becomes a little trickier when you multiply two binomials. We are still going to use the distributive property, but many students refer to the acronym, FOIL in order to remember the steps for multiplying binomials.

I am actually going to show you two ways to multiply binomials. The first way is thinking of it as another way to use the distributive property. The second way will be to use the FOIL Method. Let’s take a look at the following examples.

## How Do I Foil When I Have 3 Termshelp And Steps Are Much Appreciated :

#=24r^4-44r^3-2r^2-38r+6#

Explanation:

FOIL is a mnemonic to help enumerate all individual products of terms when multiplying two binomials. It captures the result of applying the distributive property of multiplication over addition three times:

# = a+b#

#color) = overbrace^”First”+overbrace^”Outside”+overbrace^”Inside”+overbrace^”Last”#

FOIL is not applicable to trinomials, but distributivity is.

So we could solve the given problem by:

#=8r^2+4r+6#

#=++#

#=24r^4-56r^3+12r^3+8r^2-28r^2+18r^2+4r-42r+6#

#=24r^4+r^3+r^2+r+6#

#=24r^4-44r^3-2r^2-38r+6#

Alternatively, we can write the coefficients of the #9# individual products of pairs of terms in a table and sum the reverse diagonals, to find the coefficients of the product like this:

#underlinecolor \ ” |” colorcolor8 \ colorcolor4 \ colorcolor6)#

How Do You Use The Foil Method In Algebra

The following steps demonstrate how to use FOIL on this multiplication problem.

FOIL Method. A technique for distributing two binomials. The letters FOIL stand for First, Outer, Inner, Last. First means multiply the terms which occur first in each binomial. Then Outer means multiply the outermost terms in the product.

Additionally, what is the foil method of multiplying polynomials? The FOIL method is a technique used to help remember the steps required to multiply two binomials. Remember that when you multiply two terms together you must multiply the coefficient and add the exponents. The FOIL method is shown in the diagram below.

Considering this, what is foil method and example?

The FOIL Method is a process used in algebra to multiply two binomials. The lesson on the Distributive Property, explained how to multiply a monomial or a single term such as 7 by a binomial such as . That is, what if a binomial was being multiplied by another binomial? An example of this is given below.

What is the opposite of foil in math?

Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers

Table As An Alternative To Foil

A visual memory tool can replace the FOIL mnemonic for a pair of polynomials with any number of terms. Make a table with the terms of the first polynomial on the left edge and the terms of the second on the top edge, then fill in the table with products. The table equivalent to the FOIL rule looks like this:

×

How To Do Foil Method

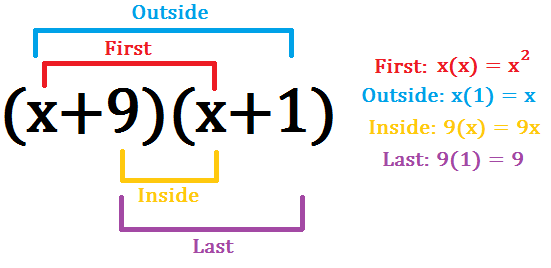
The foil method is a technique used for remembering the steps required to multiply two binomials in an organized manner.

The F-O-I- L acronym stands for first, outer, inner, and last.

Lets explain each of these terms with the help of bold letters:

• First, which means multiplying the first terms together, i.e.
• Outer means that we multiply the outermost terms when the binomials are placed side by side, i.e. .
• Inner means multiply the innermost terms together i.e. i.e. .
• Last. This implies that we multiply together the last term in each binomial, i.e., i.e. .

Read Also: Algebra 1 Age Word Problems

Multiplying Two Binomials Using The Vertical Method

The FOIL method is usually the quickest method for multiplying two binomials, but it works only for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

You start by multiplying 23 by 6 to get 138.Then you multiply 23 by 4, lining up the partial product in the correct columns.Last, you add the partial products.Now well apply this same method to multiply two binomials.

Example : Using The Distributive Property

We will use the distributive property to multiply the following binomials:

Now, that seems like a lot of work doesn’t it? That is the process for multiplying binomials, but eventually you’ll be able to complete this process without writing out each step of the distributive property. I wrote it out, in hopes that you will understand the process. You will be able to do a lot of those steps mentally!

One way to help you remember the steps to perform mentally is to remember the acronym, FOIL. If you compare each step in the first example, to the steps used in example 2 with the foil method, you will find that they are pretty much the same. Let’s take a look!

FOIL stands for:

Let’s see how we can use FOIL to multiply two binomials.

You May Like: Unit 1 Test Geometry Basics Answers Key

Examples Of How To Multiply Binomials Using The Foil Method

Example 1: Multiply the binomials \left\left using the FOIL Method.

• Multiply the pair of terms coming from the first position of each binomial.

• Multiply the outer terms when the two binomials are written side-by-side.

• Multiply the inner terms when the two binomials are written side-by-side.

• Multiply the pair of terms coming from the last position of each binomial.

• Finally, simplify by combining like terms. I see that we can combine the two middle terms with variable x.

Example 2: Multiply the binomials \left\left using the FOIL Method.

If the first presentation on how to multiply binomials using FOIL doesnt make sense yet. Let me show a different way. The idea is to expose you to different ways on how to address the same type of problem with a different approach.

• Multiply the first terms

• Multiply the inner terms

• Multiply the last terms

After applying the FOIL, we arrive at this polynomial which we can simplify by combining similar terms. The two middle x-terms can be subtracted to get a single value.

Example 3: Multiply the binomials \left\left using the FOIL Method.

Another way of doing this is to list the four partial products, and then add them together to get the answer.

• Multiply the first terms

Notice that the middle two terms cancel each other out!

Example 6: Multiply the binomials \left\left.

Solution:

• Product of the first terms

• Product of the outer terms

• Product of the inner terms

• Product of the last terms

Add the two middle x-terms, and we are done!

Solution:

What Is Foil Method In Math

FOIL MethodFOILmeansmeans

FOIL Method. A technique for distributing two binomials. The letters FOIL stand for First, Outer, Inner, Last. First means multiply the terms which occur first in each binomial. Then Outer means multiply the outermost terms in the product.

Additionally, what is foil method and example? The FOIL Method is a process used in algebra to multiply two binomials. The lesson on the Distributive Property, explained how to multiply a monomial or a single term such as 7 by a binomial such as . That is, what if a binomial was being multiplied by another binomial? An example of this is given below.

Similarly one may ask, how do you do the foil method?

The following steps demonstrate how to use FOIL on this multiplication problem.

What is the opposite of foil in math?

Reverse FOIL. “Reverse FOIL” is a method of factoring a quadratic trinomial by trial-and-error. The strategy is to determine the First and Last terms of each binomial in the factored product so the Outer and Inner products add to the middle term.

Also Check: What Does K Stand For In Math

What Is The Foil Method

Many students will start thinking of a kitchen when they first hear a mention of the term foil.

Here, we are talking about the FOIL a mathematical series of steps used to multiply two binomials. Before we learn what the term foil entails, lets take a quick review of what the word binomial is.

A binomial is simply an expression that consists of two variables or terms separated by either the addition sign or subtraction sign . Examples of binomial expressions are 2x + 4, 5x + 3, 4y 6, 7y y etc.

Tips From An Online Math Tutor: Stop Using Foil Now Before Its Too Late

Math students across the country have heard the mnemonic acronym FOIL from their school teachers. Its a tactic for calculating the product of two binomials that stands for First, Outside, Inside, Last. Here is an example of FOIL in action for multiplying the terms and :

Here we can see that the first terms of each binomial are multiplied together in orange to get x2. Then the outside terms are multiplied in yellow to get 3x. Then the inside terms are multiplied in blue to get 2x. And finally, the last terms of each binomial are multiplied in green to get 6. We add those four terms together to get our final answer of x2 + 5x + 6.

So far this looks like a good mnemonic. We got the answer we were looking for. So, whats the problem?

The issue is that FOIL only works for two binomials. As you continue in math, you will be multiplying many other terms together. It could be a binomial with a trinomial, it could be three binomials together or any different combination of polynomials. Consider these examples:

FOIL will not work for any of these cases, and memorizing it and FOIL-ing everything will prevent you from learning and mastering the math skill actually in play. And guess what? If youve made it to FOIL, youve already learned the math you need: the distributive property.

Here is an example you probably already know using the distributive property: 3

5x is just one term, so we simply distribute it to all four terms inside.

Also Check: What Are The Major Specialties In Psychology

Nowhow Do We Multiply Binomials

When multiplying binomials, you can use the FOIL method. For instance, to find the product of 2 binomials, youll add the products of the First terms, the Outer terms, the Inner terms, and the Last terms.

FIRST: multiply the first term in each set of parenthesis

OUTER: multiply the outer term in each set of parenthesis

INNER: multiply the inner term in each set of parenthesis

LAST: multiply the last term in each set of parenthesis

Using The Foil Method To Simplify

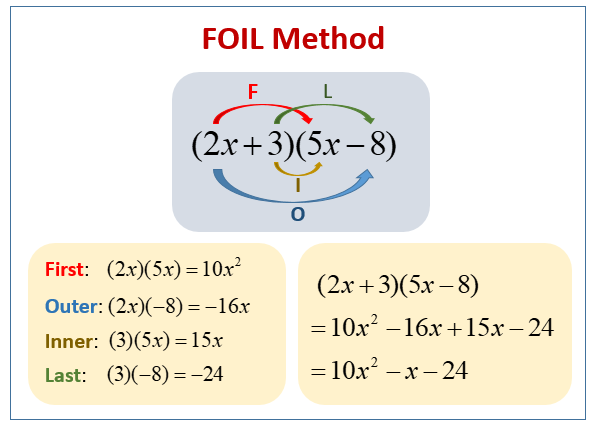
You already know how to simplify an expression like \\), right? Just use the distributive property to multiply 7 times 4x and then 7 times 3. This gives you an answer of \. Pretty simple. But – What if you have something like this: \\)? That’s where we use the FOIL method. FOIL means First, Outside, Inside, Last. That’s not too hard to remember if you say it in your head a few times.

You use FOIL to multiply the terms inside the parenthesis in a specific order: first, outside, inside, last. Here’s how to solve \\):

First – multiply the first term in each set of parenthesis:

Outside – multiply the two terms on the outside:

Inside – multiply both of the inside terms:

Last – multiply the last term in each set of parenthesis:

Now just add everything together to get \. This method only works easily with two binomials. To multiply something complicated like \\), just do FOIL on two of the binomials and then distribute the answer onto the remaining binomial.

Here are some more examples of FOIL multiplication:

You May Like: Geometry Segment And Angle Addition Worksheet

The Foul Math Method Is The Most Common Strategy For Multiplying Binomials You Can Use It As An Alternative To The Box Method

Example: Write the following in expanded form

To multiply binomials using FOIL, you must follow these steps:

Note that FOIL is an acronym that stands for FIRST-OUTER-INNER-LAST

FIRST: Multiply the first terms of each binomial together. In this case: 8 x 8 = 64

OUTER: Multiply the outer terms of each binomial together. In this case: 8 x -5x = -40x

INNER: Multiply the inner terms of each binomial together. In this case: -5x x 8 = -40x

LAST: Multiply the last terms of each binomial together. In this case: -5x x -5x = +25x^2

Now you have four terms: 64, -40x, -40x, and 25x^2

Notice that there are two like terms that can be combined as follows:

The final step is to rearrange the above expression into ax^2 + bx + c form

Answer: 25x^2 -80x +64

How Do You Distribute Binomials Using The Foil Method

Let us put this method into perspective by multiplying two binomials, and .

To find multiply * .

• Multiply the terms which appear in the first position of binomial. In this, case a and c are the terms, and their product are

= ac

• Outer is the next word after the word first. Therefore, multiply the outermost or the last terms when the two binomials are written side by side. The outermost terms are b and d.

= bd

• The term inner implies that we multiply two terms that are in the middle when the binomials are written side-by-side

= bc

• The last implies that we find the product of the last terms in each binomial. The last terms are b and d. Therefore, b * d = bd.

Now we can sum up the partial products of the two binomials beginning from the first, outer, inner, and then the last. Therefore, * = ac + ad + bc + bd.

The foil method is an effective technique because we can use it to manipulate numbers, regardless of how they might look ugly with fractions and negative signs.

Also Check: Homework 5 Angle Addition Postulate Answer Key

Setting Up The Problem

Simplifying Using The Foil Method Lessons

The FOIL Method is a process used in algebra to multiply two binomials.The lesson on the Distributive Property, explained how to multiply a monomialor a single term such as 7 by a binomial such as .

But, what if there was a binomial instead of a single term outside of theparentheses? That is, what if a binomial was being multiplied by anotherbinomial? An example of this is given below.

This is where the FOIL Method comes in. The next we will explain what the FOIL Method is and how to use it to solve thisproblem.

Don’t Miss: Structural Formula Of Ccl4

How To Multiply Binomials Using The Foil Method

This article was co-authored by our trained team of editors and researchers who validated it for accuracy and comprehensiveness. wikiHow’s Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 79,437 times.Learn more…

When multiplying two binomials you must use the distributive property to ensure that each term is multiplied by every other term. This can sometimes be a confusing process, as it is easy to lose track of which terms you have already multiplied together. You can use FOIL to multiply binomials using the distributive property in an organized way.XResearch sourceBy simply remembering the words in the acronym, this method will help you multiply binomials quickly.

How Do You Multiply Binomials Using The Foil Method

To master the foil method better, we shall solve a few examples of binomials.

Example 1

Multiply

Solution

• Begin, by multiplying together, the first terms of each binomial

= 2x * 3x = 6x 2

• Now multiply the outer terms.

= 2x * -1= -2x

• Now multiply the inner terms.

= * = 9x

• Finally, multiply the last team in each binomial together.

= * = 3

• Sum up the partial products starting from the first to last product and collect the like terms

= 6x 2 + + 9x +

= 6x 2 + 7x 3.

Use the foil method to solve:

Solution

• Multiply the inner terms of the binomial:

= 3 * -2x = 6x

• Finally, multiply the last terms:

= 3 * 8 = -24

• Find the sum of the partial products and collect the like terms:

= 14x 2 + + 6x +

= 14x 2 56x 24

Multiply

Solution

• Multiply the first terms together:

= * = 2x 2

• Multiply the outermost terms of each binomial:

= * = 9x

• Multiply the inner terms of the binomial:

= * = 6x

• Multiply the last terms of each binomial:

= * = 27

• Sum up the products following the foil order and collect the like terms:

= 2x 2 9x -6x + 27

= 2x 2 15x +27

Multiply

Solution

• In this case, the operations are broken down into smaller units, and the results combine:
• Begin by multiplying the first terms:

= * 3x = 3x 2

• Multiply the outer terms of each binomial:

= * = 2xy + x

• Multiply the inner terms of each binomial:

= = 3xy 12x

• Now finish by multiplying the last terms:

Since the last terms area gain two binomials Sum up the products:

= 3x 2 + 2xy + x + 3xy 12x +

= 3x 2 + 5xy 11x +

• * = 2y2

You May Like: Algebra Road Trip Project Answer Key