Example Of Theorem In Geometry

What Is An Example Of A Theorem

The definition of a theorem is an idea that can be proven or shown as true. An example of a theorem is the idea that mixing yellow and red make orange. YourDictionary definition and usage example.

How many theorems are there in geometry?

Naturally, the list of all possible theorems is infinite, so I will only discuss theorems that have actually been discovered. Wikipedia lists 1,123 theorems, but this is not even close to an exhaustive listit is merely a small collection of results well-known enough that someone thought to include them.

What Is The Interior Angle Of A Triangle

In geometry, the interior angles of a triangle are the angles that are formed inside a triangle.

Interior angles have the following properties:

• The sum of interior angles is 180 degrees .
• All interior angles of a triangle are more than 0° but less than 180°.
• The bisectors of all three interior angles intersect inside a triangle at a point called the in-center, which is the center of the in-circle of the triangle.
• The sum of each interior angle and exterior angle is equal to 180° .

Triangle Theorems Lesson & Examples

1 hr 10 min

• Introduction SSS and SAS Similarity Postulates
• 00:00:19 Overview of Proportionality Statements for Segments Parallel to a Side of a Triangle
• 00:15:24 Find the value of x given similar triangles
• 00:28:42 Given three parallel lines cut by two transversals, find the value of x
• 00:31:36

• Determine whether the triangles are similar, and create a similarity statement
• 00:51:37 Find the unknown value given similar triangles
• 01:02:36 Find the unknown value or create the proportion for finding perimeter
• 01:10:16 Given similar triangles, find the perimeter
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Recommended Reading: Kuta Software Infinite Geometry The Segment Addition Postulate Answer Key

What Is The Triangle Angle Sum Theorem

One common property about triangles is that all three interior angles add up to 180 degrees. This now brings us to an important theorem in geometry known as Triangle Angle Sum Theorem.

According to the Triangle Angle Sum Theorem, the sum of the three interior angles in a triangle is always 180°.

We can this as:

a + b + c = 180°

Geometry Postulates And Theorems List With Pictures

Some of the worksheets below are Geometry Postulates and Theorems List with Pictures, Ruler Postulate, Angle Addition Postulate, Protractor Postulate, Pythagorean Theorem, Complementary Angles, Supplementary Angles, Congruent triangles, Legs of an isosceles triangle,

Once you find your worksheet, you can either click on the pop-out icon or download button to print or download your desired worksheet. Please note that you can also find the download button below each document.

Geometry with Applications and Proofs.

Theorem, Postulate and Corollary List : Ruler Postulate, Segment Addition Postulate, Segment Congruence, Protractor Postulate,

Geometry Definitions, Postulates and Theorems : Complementary Angles, Supplementary Angles, Theorem, Congruent triangles, Legs of an isosceles triangle,

Geometry Postulates and Theorems List with Pictures : Angle Addition Postulate, Triangle, Parallels, Circles,

Theorems, Postulates, and Properties for Use in Proofs : Triangle Congruency Methods, SAS postulate, SSS postulate, ASA postulate, Linear Pair Postulate, Angle Addition Postulate,

A summary of definitions, postulates, algebra rules, and theorems : definition of mid-point and segment bisector, definition of Adjacent Angles, definition of Vertical Angles,

Tools of Geometry : Segment Addition Postulate, Protractor Postulate, Midpoint Formula on a Number Line, Law of Syllogism, Vertical Angles Theorem,

Geometry Handbook : Parallelogram Proofs, Pythagorean Theorem,

Recommended Reading: What Is The Molecular Geometry Of Ccl4

Divergence Of The Prime Reciprocal Series

corollaryprime_harmonic_series_diverges:"¬convergent "

The more precise asymptotic estimate given by Mertens Second Theorem is also available:

theoremmertens_second_theorem:" - ln  - meissel_mertens)  O"

How To Find The Interior Angles Of A Triangle

When two interior angles of a triangle are known, it is possible to determine the third angle using the Triangle Angle Sum Theorem. To find the third unknown angle of a triangle, subtract the sum of the two known angles from 180 degrees.

Lets take a look at a few example problems:

Example 1

Triangle ABC is such that, A = 38° and B = 134°. Calculate C.

Solution

A + B + C = 180°

Hence, the missing angles are 60° and 55°

Example 6

Calculate the value of x for a triangle whose angles are x°, ° and °.

Solution

Sum of interior angles = 180°

x° + ° + ° = 180°

Simplify.

x + x + 2x + 20° + 40° = 180°

4x + 60° = 180°

Subtract 60 from both sides.

4x + 60° 60°= 180° 60°

4x = 120°

Now divide both sides by 4.

4x/4 = 120°/4

Therefore, the angles of the triangle are 30°, 50°, and 100°.

Example 7

Find the missing angles in the diagram below.

Solution

Triangle ADB and BDC are isosceles triangles.

DBC = DCB = 50°

Also Check: Who Are Paris Jackson’s Biological Parents

Thales Theorem Explanation & Examples

After we have gone through the Inscribed Angle Theorem, it is time to study another related theorem, which is a special case of Inscribed Angle Theorem, . Like Inscribed Angle Theorem, its definition is also based on diameter and angles inside a circle.

In this article, you learn:

• The Thales theorem,
• How to solve the Thales theorem and
• How to solve the Thales theorem with only one side

History Of The Pythagorean Theorem

Pythagoras of Samos was born on the island of Samos in Greece and traveled extensively in Egypt, learning mathematics and other things. More details about how his first years were are unknown. Pythagoras began to be recognized and to form a status by founding a group known as the Brotherhood of Pythagoras, whose objective was the study of mathematics. The brotherhood of Pythagoras had various aspects of a cult such as symbols, rituals and prayers. Furthermore, Pythagoras believed that number governs the universe, and members of the Pythagorean group gave numerical values to many objects and ideas. These numerical values, in turn, were endowed with mystical and spiritual qualities.

You May Like: Is Ap Human Geography Hard

Triangle Sum Theorem Explanation & Examples

We know that different triangles have different angles and side lengths, but one thing is fixed that each triangle is composed of three interior angles and three sides that can be of the same length or different lengths.

For instance, a right triangle has one angle that is exactly 90 degrees and two acute angles.

Isosceles triangles have two equal angles and two equal side lengths. Equilateral triangles have the same angles and same side lengths. Scalene triangles have different angles and different side lengths.

Even though all of these triangles differ in angles or side lengths, they all follow the same rules and properties.

In this article, youll learn about:

• The Triangle Sum Theorem,
• Interior angles of a triangle, and
• How to use the Triangle Sum Theorem to find the interior angles of a triangle?

How To Solve The Thales Theorem

• To prove the Thales theorem, draw a perpendicular bisector of
• Let point M be the midpoint point of line AC.
• Also let MBA = BAM = and MBC =BCM =
• Line AM = MB = MC = the radius of the circle.
• AMB and MCB are isosceles triangles.

+ + + = 180°

Factor the equation.

2 + 2 = 180°

2 = 180°

Divide both sides by 2.

+ = 90°.

Therefore, ABC = 90°, hence proved

Lets work out a few example problems involving the Thales theorem.

Example 1

Given that point O is the center of the circle shown below, find the value of x.

Solution

Given that the line XY is the diameter of the circle, then by Thales theorem

XYZ = 90°.

Sum of interior angles of a triangle = 180°

90° + 50° + x =180°

Hence, the diameter of the circle is 10 cm

Example 3

Find the measure of angle PQR in the circle shown below. Assume point R is the center of the circle.

Solution

Triangle RQS and PQR are isosceles triangles.

RQS =RSQ =64°

By Thales theorem, PQS = 90°

So, PQR = 90° 64°

Hence, the measure of angle PQR is 26°.

Example 4

Which one of the following statements is true about the definition of the Thales theorem?

A. The central angle is twice the measure of the inscribed angle

B. An angle inscribed in a half-circle will be a right angle.

C. The diameter of a circle is the longest chord.

D. The diameter of a circle is twice the length of the radius.

Solution

B. An angle inscribed in a half-circle will be a right angle.

Example 5

You May Like: Algebra 1 Age Word Problems

What Is An Example Of A Theorem In Geometry

ExampleTheoremtriangle

. Also asked, what is a theorem in geometry?

A theorem is a statement that can be demonstrated to be true by accepted mathematical operations and arguments. In general, a theorem is an embodiment of some general principle that makes it part of a larger theory. The process of showing a theorem to be correct is called a proof.

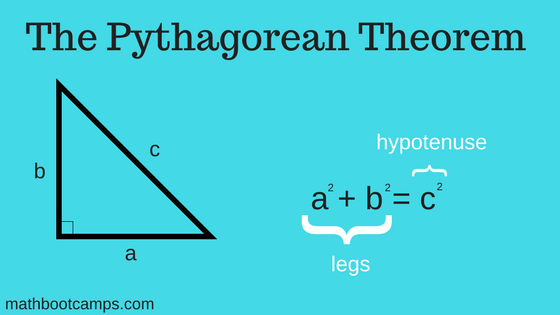
Secondly, what are some examples of Pythagorean Theorem? Pythagorean theoremThe square of the length of the hypotenuse of a right triangle is the sum of the squares of the lengths of the two sides. This is usually expressed as a2+b2 = c2. Integer triples which satisfy this equation are Pythagorean triples. The most well known examples are and .

Accordingly, what is an example of a theorem?

The definition of a theorem is an idea that can be proven or shown as true. An example of a theorem is the idea that mixing yellow and red make orange. YourDictionary definition and usage example.

How many theorems are there in geometry?

Naturally, the list of all possible theorems is infinite, so I will only discuss theorems that have actually been discovered. Wikipedia lists 1,123 theorems, but this is not even close to an exhaustive listit is merely a small collection of results well-known enough that someone thought to include them.

Maths Theorems For Class 10

In Class 10 Maths, several important theorems are introduced which forms the base of mathematical concepts. Class 10 students are required to learn thoroughly all the theorems with statements and proofs, not only to score well in the board exam but also to create a stronger foundation in the subject. Some important maths theorems for Class 10 are listed below.

Recommended Reading: Blanket Jackson Biological Dad

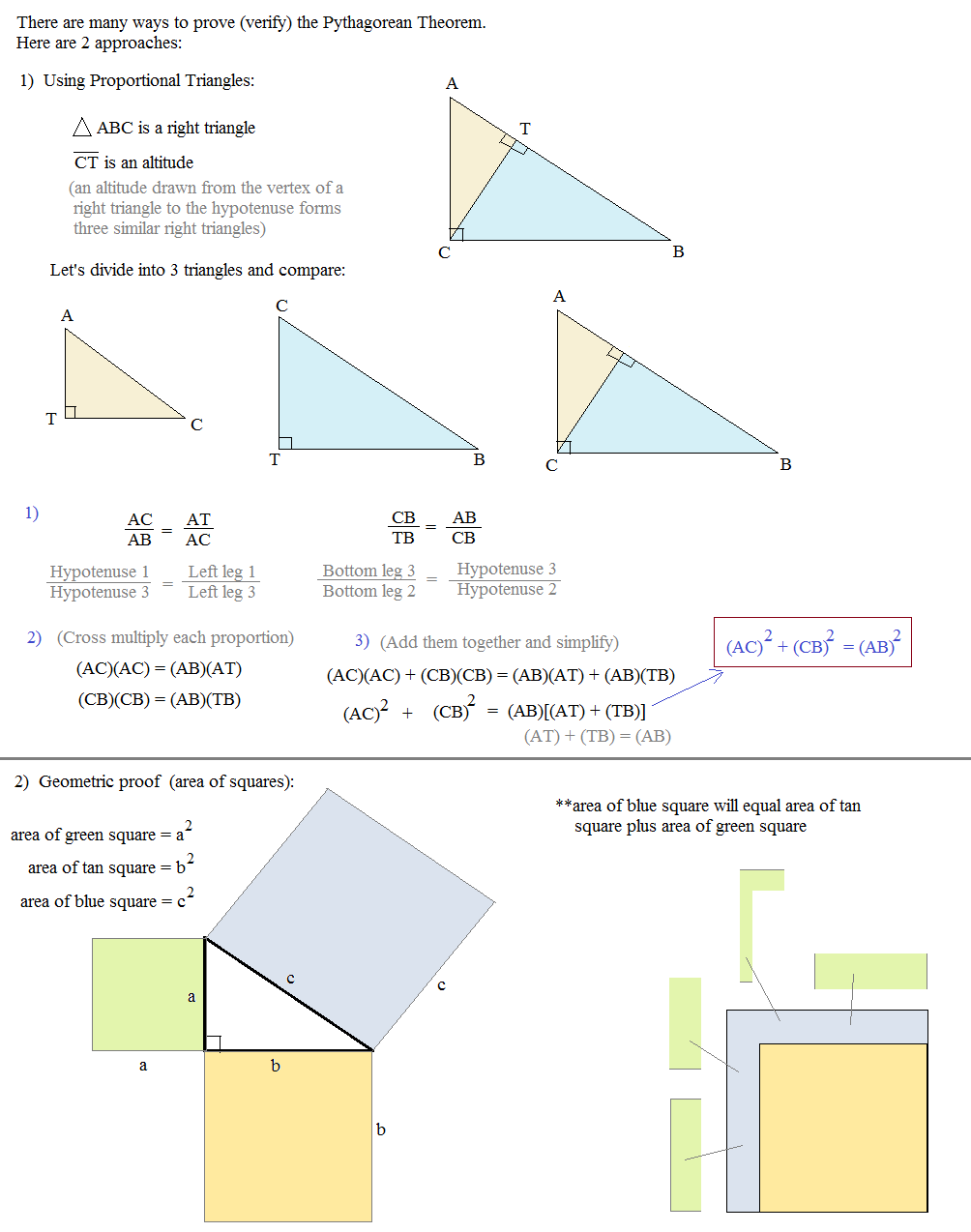
Applying The Pythagorean Theorem

In the examples below, we will see how to apply this rule to find any side of a right triangle triangle. As in the formula below, we will let a and b be the lengths of the legs and c be the length of the hypotenuse. Remember though, that you could use any variables to represent these lengths.

In each example, pay close attention to the information given and what we are trying to find. This helps you determine the correct values to use in the different parts of the formula.

Why Are Theorems Important In Maths

Theorems are of significance and are considered as absolute truths. Theorems not only help to solve mathematical problems easily but their proofs also help to develop a deeper understanding of the underlying concepts. For students, theorems not only form the foundation of basic mathematics but also helps them to develop deductive reasoning when they completely understand the statements and their proofs.

Read Also: Who Are Paris Jackson’s Biological Parents

The Factor And Remainder Theorems

lemmalong_div_theorem:assumes"g  carrier P"and"f  carrier P"and"g \< ^bsub> P\< ^esub> "shows"q r .            \< ^bsub> R\< ^esub> k \< ^bsub> P\< ^esub>  f = g \< ^bsub> P\< ^esub>  q \< ^bsub> P\< ^esub>  r         "

Example: A Theorem And A Corollary

Theorem:

Corollary:

Following on from that theorem we find that where two lines intersect, the angles opposite each other are equal .

Angle a = angle c

Angles a and b add to 180° because they are along a line:

a + b = 180°

Likewise for angles b and c

b + c = 180°

And since both a and c equal 180° b, then

a = c

And a slightly more complicated example from Geometry:

Don’t Miss: Geometry Segment And Angle Addition Worksheet Answers

Applications Of Thales Theorem

In geometry, none of the topics are without any real-life use. Therefore, Thales Theorem also has some applications:

• We can accurately draw a tangent to a circle using Thales Theorem. You can use a set square for this purpose.
• We can accurately find the center of the circle using the Thales Theorem. The tools used for this application are a set square and a sheet of paper. Firstly, you have to place the angle at the circumferencethe intersections of two points with circumference state the diameter. You can repeat this using different pair of points, which will give you another diameter. The intersection of diameters will give you the center of the circle.

The Hundred Greatest Theorems

Also Check: Ccl4lewis Structure

How To Find The Hypotenuse

So you may be wondering: how do I find the hypotenuse? It’s simple! You just use the pythagorean theorem above! It is crucial to helping you figure out the hypotenuse in a right angle triangle. You will first need the other two sides before you can figure out the longer hypotenuse side of the triangle, but it’s easy once you’ve got that down!

Chapter : Theorem: Pythagorean Theorem

The square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides.

\ with \

Construction: draw \.

Converse: theorem of Pythagoras

If the square of one side of a triangle is equal to the sum of the squares of the other two sides of the triangle, then the angle included by these two sides is a right angle.

You May Like: Who Are Paris Jackson’s Biological Parents

Example: A Theorem A Corollary To It And Also A Lemma

Theorem:

Proof: Join the center O to A.

Triangle ABO is isosceles , so:

b°

Triangle ACO is isosceles, so:

c°

Replace b + c with a, we get:

Angle BAC = a° and Angle BOC = 2a°

And we have proved the theorem.

Corollary

Keeping the endpoints fixed … … the angle a° is always the same, no matter where it is on the circumference:

So, Angles Subtended by the Same Arc are equal.

Lemma

In the special case where the central angle forms a diameter of the circle:

2a° = 180° , so a° = 90°

So an angle inscribed in a semicircle is always a right angle.

Another example, related to Pythagoras’ Theorem:

The Top 100 Theorems In Isabelle

The following are the theorems from this list proved so far in the Isabelle proof assistant.

If you have proved additional ones or know of any, please so I can add them here.

If the theorem is not part of the Isabelle distribution, the entry will usually contain a link to the repository that does. The list does not automatically track the most recent version of each theorem. If you find one that that is out of date and would like me to update it, let me know.

Recommended Reading: Segment Addition Postulate Coloring Activity

Informal Account Of Theorems

Logically, many theorems are of the form of an indicative conditional: If A, then B. Such a theorem does not assert B only that B is a necessary consequence of A. In this case, A is called the hypothesis of the theorem , and B the of the theorem. The two together are called the proposition or statement of the theorem . Alternatively, A and B can be also termed the antecedent and the consequent, respectively. The theorem “If n is an even natural number, then n/2 is a natural number” is a typical example in which the hypothesis is “n is an even natural number”, and the conclusion is “n/2 is also a natural number”.

In order for a theorem be proved, it must be in principle expressible as a precise, formal statement. However, theorems are usually expressed in natural language rather than in a completely symbolic formwith the presumption that a formal statement can be derived from the informal one.

It is common in mathematics to choose a number of hypotheses within a given language and declare that the theory consists of all statements provable from these hypotheses. These hypotheses form the foundational basis of the theory and are called axioms or postulates. The field of mathematics known as proof theory studies formal languages, axioms and the structure of proofs.

Equal Arcs Subtend Equal Angles

From the theorem above we can deduce that if angles at the circumference of a circle are subtended by arcs of equal length, then the angles are equal. In the figure below, notice that if we were to move the two chords with equal length closer to each other, until they overlap, we would have the same situation as with the theorem above. This shows that the angles subtended by arcs of equal length are also equal.

Recommended Reading: Who Are Paris Jackson’s Biological Parents