What Is Congruent In Geometry

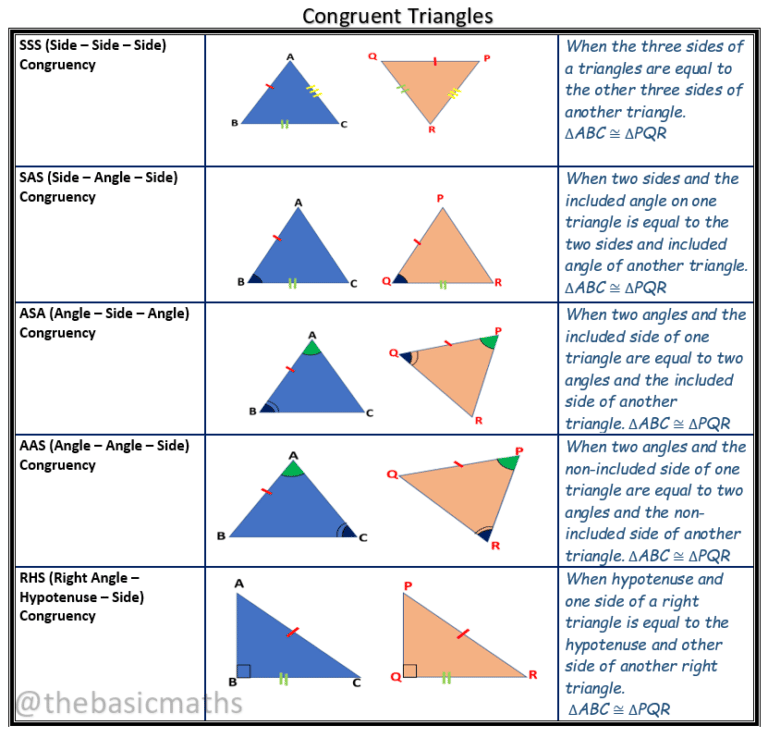
Rules For Triangle Congruency

Congruent triangles are triangles that have the same size and shape.This means that the corresponding sides are equal and the corresponding angles are equal.

We can tell whether two triangles are congruent without testing all the sides and all the angles ofthe two triangles. In this lesson, we will consider the four rules to prove triangle congruence.They are called the SSS rule, SAS rule, ASA rule and AAS rule.In another lesson, we will consider a proof used for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.

The following diagrams show the Rules for Triangle Congruency: SSS, SAS, ASA, AAS and RHS. Take notethat SSA is not sufficient for Triangle Congruency. Scroll down the page for more examples, solutionsand proofs.

What Are Congruent Line Segments

Congruent line segments are 1-dimensional geometrical figures having equal measures. The word “congruent” with respect to congruent lines in geometry is defined as the equality between the two line segments. Two lines are said to be congruent when they have the same length. Congruent segments are superimposable figures, which completely overlap when placed one over the other. On turning, flipping, or rotating the congruent segments, they still remain to be congruent. The symbol used to depict congruence between any two congruent line segments is .

To brief it, congruent segments is just another name given to congruent line segments or congruent lines in geometry. All three terms are mathematically the same. Now, let us look into some examples of congruent line segments we find in mathematics.

Examples of congruent line segments:

• Sides of an equilateral triangle.

Let’s look into the diagram below showing congruent line segments.

Here line segment PQ XY since the double vertical bars on each line segment, PQ and XY depict their equality.

Congruent Meaning In Geometry

The word ‘congruent’ means ‘exactly equal’ in terms of shape and size. Even when we turn, flip, or rotate the shapes, they remain equal. For example, draw two circles of the same radius, then cut them out and place them on one another. We will notice that they will superimpose each other, that is, they will be placed completely over each other. This shows that the two circles are congruent. The following circles are said to be congruent since they have an equal radius, and they can be placed exactly over one another. The symbol that is used to show the congruence of figures is “”. Since circle A is congruent to circle B, we can express this fact as follows: Circle A Circle B.

Read Also: How To Find Time In Physics

Congruent Angle Sample Questions

Here are a few sample questions going over congruent angles.

Question #1:

Angles 1 and 2 are corresponding angles. If the measure of Angle 2 is 67°, what is the measure of Angle 1?

164°

Question #4:

The city of Seattle is building a walking path that crosses over a pair of railroad tracks. The walking path is represented by the transversal t in the image below. The railroad tracks are represented by the parallel lines l and m. If the city wants to have the walking path cross the tracks at a 135° angle , what will the values of Angles 2, 3, and 4 be?

2 = 45° 3 = 135° 4 = 45°

2 = 45° 3 = 45° 4 = 135°

2 = 145° 3 = 45° 4 = 45°

2 = 180° 3 = 45° 4 = 45°

Answer:

1 and 4 are congruent because they are vertical angles. If 1 equals 135°, then 2 must be equal to 45° because their sum needs to be 180° in order to form a straight line. Now that we know 2 equals 45°, we also know that 3 equals 45° because they are vertical angles.

Question #5:

Kelcy has a rectangular garden that she wants to divide equally into two sections diagonally. One section will be for carrots and the other section will be for kale. She separates the garden into two triangular pieces similar to the image below. If the measure of DCA is 40° what is the measure of CAB?

Definition Of Congruence In Analytic Geometry

In a Euclidean system, congruence is fundamental it is the counterpart of equality for numbers. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.

A more formal definition states that two subsetsA and B of Euclidean spaceRn are called congruent if there exists an isometryf : Rn â Rn ) with f = B. Congruence is an equivalence relation.

Don’t Miss: What Are All The Laws Of Physics

Congruent Triangle Theorem And Postulates

Two triangles are said to be congruent if they have same shape and same size. When triangles are congruent corresponding sides and corresponding angles are congruent .

There are two theorems and three postulates that are used to identify congruent triangles.

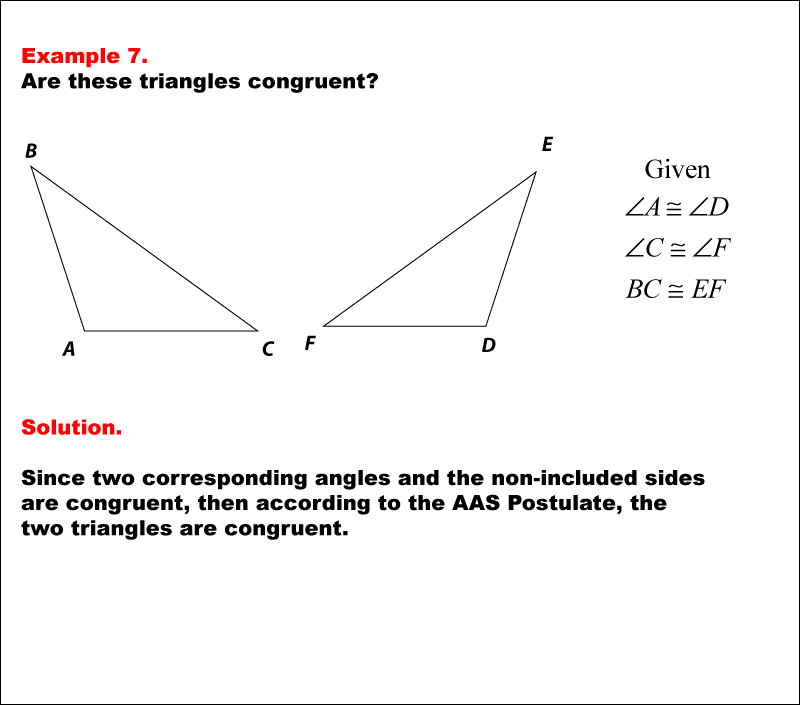
Angle-Angle-Side Theorem

As per this theorem the two triangles are congruent if two angles and a side not between these two angles of one triangle are congruent to two corresponding angles and the corresponding side not between the angles of the other triangle.

Example:

Hypotenuse-Leg Theorem

If the hypotenuse and one of the legs of a right triangle are congruent to hypotenuse and corresponding leg of the other right triangle, the two triangles are said to be congruent.

Side-Side-Side Postulate

If all three sides of a triangle are congruent to corresponding three sides of other triangle then the two triangles are congruent.

Angle-Side-Angle Postulate

According to this postulate the two triangles are said to be congruent if two angles and the side between these two angles of one triangle are congruent to corresponding angles and the included side of the other triangle.

Side-Angle-Side Postulate

If two sides and the included angle of one triangle are congruent to the corresponding two sides and the included angle of a second triangle, then the two triangles are congruent.

Congruent Triangles On A Sphere

As with plane triangles, on a sphere two triangles sharing the same sequence of angle-side-angle are necessarily congruent . This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point thus ASA is valid.

The congruence theorems side-angle-side and side-side-side also hold on a sphere in addition, if two spherical triangles have an identical angle-angle-angle sequence, they are congruent .

The plane-triangle congruence theorem angle-angle-side does not hold for spherical triangles. As in plane geometry, side-side-angle does not imply congruence.

You May Like: How Did Geography Affect Ancient Greece

What Are The Properties Of Congruence

The properties of congruence are applicable to lines, angles, and figures. They can be listed as follows: Reflexive property, Symmetric property, and Transitive property.

• The reflexive property of congruence says that a line segment, an angle, or a shape is always congruent to itself. For example, PP
• The symmetric property says that if one figure is congruent to another, then the second one is also congruent to the first. For any two angles P and Q, if P Q, then Q P.
• The transitive property of congruence states that if line 1 is congruent to line 2, and line 2 is congruent to line 3, then line 1 is also congruent to line 3.

Congruent Meaning In Maths

The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.

Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is the same as the other.

Recommended Reading: Definition Of Equilateral Triangle In Geometry

Congruent And Similar Triangles

• Congruent and Similar Triangles

In mathematics, we say that two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection. If the objects also have the same size, they are congruent.

Contents

• Problem Solving – Intermediate

Three Ways To Prove Triangles Congruent

A video lesson on SAS, ASA and SSS.

Read Also: What Is The Importance Of Measurement In Physics

Using Two Column Proofs To Prove Triangles Congruent

Triangle Congruence by SSSHow to Prove Triangles Congruent using the Side Side Side Postulate? If three sides of one triangle are congruent to three sides of another triangle, then the two trianglesare congruent.

Triangle Congruence by SASHow to Prove Triangles Congruent using the SAS Postulate? If two sides and the included angle of one triangle are congruent to two sides and the included angle ofanother triangle, then the two triangles are congruent.

Prove Triangle Congruence with ASA PostulateHow to Prove Triangles Congruent using the Angle Side Angle Postulate? If two angles and the included side of one triangle are congruent to two angles and the included sideof another triangle, then the two triangles are congruent.

Prove Triangle Congruence by AAS PostulateHow to Prove Triangles Congruent using the Angle Angle Side Postulate? If two angles and a non-included side of one triangle are congruent to two angles and a non-includedside of another triangle, then the two triangles are congruent.

Congruent Figures Lesson & Examples

41 min

• Introduction to identifying congruent figures

• Write a congruence statement for the pair of congruent figures
• 00:18:54 Write a congruence statement for the pair of congruent figures
• 00:27:30 Find x and y given pair of congruent quadrilaterals
• 00:31:04 Find x and y given pair of congruent triangles
• 00:33:43 Give the reason for each statement
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Also Check: What Is The Physical Geography Of Africa

How To Prove Two Line Segments Are Congruent

Given two line segments, the lengths can be measured using a ruler which helps us to compare their equality. If the lengths of two line segments are equal, they are known to be congruent. For example, sides of an equilateral triangle are congruent as all the three sides are of equal measure. The distance between two lines which are line segments and are congruent have a distance of zero units between them.

When Is A Line Segment Congruent To Itself

When a line segment is compared to itself, the line segment is congruent to itself since they exactly measure the same. This is the reflexive property followed by a congruent line segment. For example, consider a line segment, MN of length 7.5 cm. When this line segment is compared to itself they become congruent i.e., MN MN.

Recommended Reading: What Is The Definition Of Potential Energy In Physics

What Are Congruent Lines Angles

When two line segments exactly measure the same, they are known as congruent lines. For example, two line segments XY and AB have a length of 5 inches and are hence known as congruent lines. When two angles exactly measure the same, they are known as congruent angles. For example, the internal angles of a square are congruent as each angle measures 90º.

Congruent Definition In Geometry

The word “congruent” is an adjective, and it describes these two squares:

These are congruent squares their corresponding parts are identical, so they have congruency. The word “congruency” is the noun for what these figures have. Congruent figures have congruency. Whether you have just two figures or a whole chessboard of congruent squares, they are all congruent

Read Also: Who Coined The Term Geography

Determining Congruence Of Polygons

For two polygons to be congruent, they must have an equal number of sides . Two polygons with n sides are congruent if and only if they each have numerically identical sequences side-angle-side-angle-… for n sides and n angles.

Congruence of polygons can be established graphically as follows:

• First, match and label the corresponding vertices of the two figures.
• Second, draw a vector from one of the vertices of the one of the figures to the corresponding vertex of the other figure. Translate the first figure by this vector so that these two vertices match.
• Third, rotate the translated figure about the matched vertex until one pair of corresponding sides matches.
• Fourth, reflect the rotated figure about this matched side until the figures match.

If at any time the step cannot be completed, the polygons are not congruent.

Construction Of Two Congruent Angles

Let’s learn the construction of two congruent angles step-wise.

Step 1- Draw two horizontal lines of any suitable length with the help of a pencil and a ruler or a straightedge.

Step 2- Take any arc on your compass, less than the length of the lines drawn in the first step, and keep the compass tip at the endpoint of the line. Draw the arc keeping the lines AB and PQ as the base without changing the width of the compass.

Step 3 – Keep the compass tip on point D and expand the legs of the compass to draw an arc of any suitable length. Draw that arc and repeat the same process with the same arc by keeping the compass tip on point S.

Step 4- Draw lines that will join AC and PR.

This is how we get two congruent angles in geometry, CAB, and RPQ.

Don’t Miss: What Do You Do In Chemistry

What Is Congruent Segment Midpoint

The congruent segment midpoint is defined as that point on a line segment that exactly divides the line segment into two parts of equal length and hence the two newly formed segments are congruent to each other. For example, for a line segment of length 10 cm, the midpoint will exactly be at 5 cm and the newly formed segments will be 5 cm each.

What Are Congruent Angles

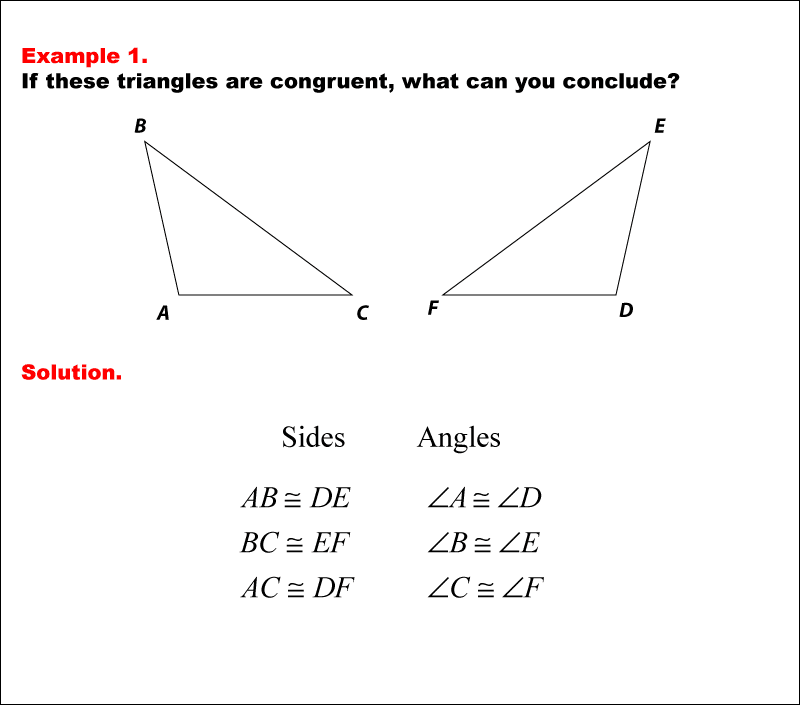
In mathematics, the definition of congruent angles is “angles that are equal in the measure are known as congruent angles”. In other words, equal angles are congruent angles. It is denoted by the symbol “”, so if we want to represent A is congruent to X, we will write it as A X. Look at a congruent angles example given below.

In the above image, both the angles are equal in measurement . They can completely overlap each other. So, as per the definition, we can say that both the given angles are congruent angles.

Don’t Miss: Big Ideas Math Geometry 4.5 Answers

Congruent And Similar Figures

There is a difference between congruent and similar figures. Congruent figures have the same corresponding side lengths and the corresponding angles are of equal measure. However, similar figures may have the same shape, but their size may not be the same.

For example, observe the following triangles which show the difference between congruent and similar figures. In the congruent figures, we can see that all the corresponding sides and angles are of equal measure. However, if we notice the similar figures, we see that the corresponding angles are of equal measure, but the sides are not of equal length.

Difference Between Congruent Figures And Similar Figures

The significant difference between congruent figures and similar figures is that:

As per the above diagram, Congruent Figures are represented by ABC and DEF, whereas Similar Figures are represented by MNO and XYZ

In regards to Congruent Figures,

Side AC = DF, AB = DE and BC = EF,

A = D, B = E and C = F

Therefore, ABC DEF, as both the corresponding angles and the lengths of the corresponding side are equal to each other.

Whereas, with respect to Similar Figures.

Only the angles are equal to each other, which are M = X, N = Y and O = Z.

The length of the corresponding sides are not equal to each other.

Hence, MNO and XYZ are similar to each other.

However, they are not congruent to each other.

You May Like: What Is Potential Difference In Physics