What Does Hm Mean In Math

What Is The Comparison Between The Arithmetic Geometric And Harmonic Means

Mean | Types of Mean | Relation between AM, GM, HM |

Algebra is the branch of mathematics that deals with numbers and symbols and provides the rules to manipulate these symbols and numbers. An algebraic expression is formed of numbers, variables, and mathematical operators. Example: 6y+2 is an algebraic expression. Comparing numerical values is an important aspect of mathematics, and algebra helps us deal with this. Mean is another entity that is used for finding relationships between Numbers/ Variables. There are three kinds of mean available: Arithmetic Mean, Geometric Mean, Harmonic Mean in algebraic mathematics which helps us in calculating Mean. Now, we will discuss the three means in mathematics: Arithmetic Mean, Geometric Mean, Harmonic Mean, and compare three of them on the basis of magnitude.

Arithmetic Mean

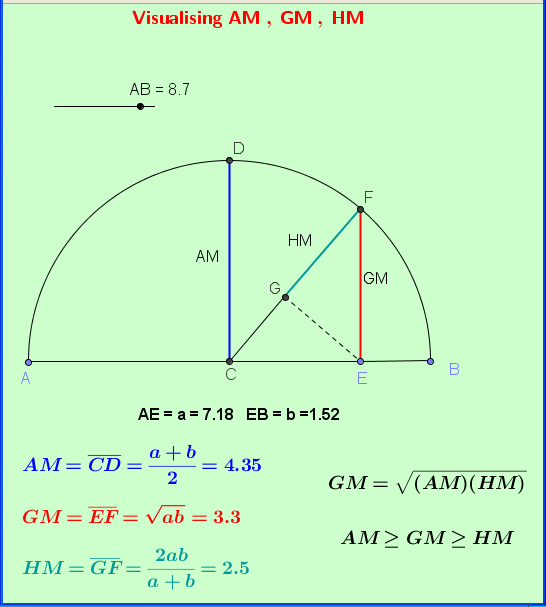
In mathematics, arithmetic Mean evaluates the total sum of the numbers upon the total count of numbers. Arithmetic Mean in simple terms is basically the average of all the given numbers whose Arithmetic Mean needs to be calculated. Consider two variables R and S then the arithmetic mean of these variables would be given by the formula:

Let the total number of entities under consideration, here the two variables are entities so, assign entities the value of 2.

AM = /N

= /2

Geometric Mean

Let the total number of entities under consideration, here the two variables are entities so, assign entities the value of 2.

GM = 1/N

= 1/2

Harmonic Mean

Relationship With Other Means

proof without wordsmaxroot mean square quadratic mean arithmetic mean geometric mean harmonic meanminab

The harmonic mean is one of the three Pythagorean means. For all positive data sets containing at least one pair of nonequal values, the harmonic mean is always the least of the three means, while the arithmetic mean is always the greatest of the three and the geometric mean is always in between.

It is the special case Mâ1 of the power mean:

H â 1 ,x_,\ldots ,x_\right)=M_\left=^+x_^+\cdots +x_^}}}

Since the harmonic mean of a list of numbers tends strongly toward the least elements of the list, it tends to mitigate the impact of large outliers and aggravate the impact of small ones.

The arithmetic mean is often mistakenly used in places calling for the harmonic mean. In the speed example below for instance, the arithmetic mean of 40 is incorrect, and too big.

The harmonic mean is related to the other Pythagorean means, as seen in the equation below. This can be seen by interpreting the denominator to be the arithmetic mean of the product of numbers n times but each time omitting the j-th term. That is, for the first term, we multiply all n numbers except the first for the second, we multiply all n numbers except the second and so on. The numerator, excluding the n, which goes with the arithmetic mean, is the geometric mean to the power n. Thus the n-th harmonic mean is related to the n-th geometric and arithmetic means. The general formula is

How To Choose The Correct Mean

We have reviewed three different ways of calculating the average or mean of a variable or dataset.

The arithmetic mean is the most commonly used mean, although it may not be appropriate in some cases.

Each mean is appropriate for different types of data for example:

If values have the same units: Use the arithmetic mean.
If values have differing units: Use the geometric mean.
If values are rates: Use the harmonic mean.

The exceptions are if the data contains negative or zero values, then the geometric and harmonic means cannot be used directly.

Don’t Miss: What Is Biological Pest Control

Relation To Other Means

The harmonic mean of x, … , x is equal to the reciprocal of the arithmetic mean of 1/x, … , 1/x.

If there are only two numbers, you can compute the harmonic mean as the ratio of the geometric mean squared and the arithmetic mean: H = G2 / A.

For any list of positive numbers, the harmonic mean exceeds neither the arithmetic and nor the geometric mean.

How To Calculate Harmonic Mean

Below are steps to obtain the harmonic mean of a particular data set:

For a given set of data say \.

Step 1: Find the reciprocal of every value as \.

Step 2: Obtain the average of reciprocal values.

Step 3: Calculate the reciprocal of the average received by the formula:

Check out this article on probability.

Section 3 Of : How To Use Hm

Talk about a person who is hard to please. When you’re annoyed at someone for being too needy, demanding, or financially draining, it’s totally reasonable to discuss those frustrations with another person. Message a trustworthy friend about your troubles over Snapchat, text, or another app.

You: “Ugh, my date last night was a bust! They were so HM, it was ridiculous.”

Them: “Oh no! I’m sorry. I’m here if you need to vent about it.”

Harmonic Mean Vs Geometric Mean

Both harmonic mean and geometric mean are measures of central tendencies. Here are the differences between these two means:

Harmonic mean	Geometric Mean
Given a data set, the harmonic mean can be evaluated by dividing the total number of terms by the sum of the reciprocal terms.	When we are given a data set consisting of n number of terms then we can find the geometric mean by multiplying all the terms and taking the nth root.
Its value is always lesser than the other two means.	Its value is always greater than the harmonic mean but lesser than the arithmetic mean.
It is the arithmetic mean of the data set with certain reciprocal transformations.	It can be thought of as the arithmetic mean with certain log transformations.
Example: If we are given a sequence 1, 2, 4, 7. n = 4	GM = 1/4 = 2.735

Recommended Reading: What Is Molarity In Chemistry

Degree Of Variation Between The Means

If all the values in a data set are the same, then all the three means will be identical. As the variability in the data increases, the difference among these means also increases. Arithmetic mean is always greater than the GM, which in turn is always greater than the HM.

The other measures of central tendency and the guidelines for selecting the appropriate measure of central tendency will be dealt with in the subsequent issue.

Concept Of Harmonic Mean

Arithmetic Mean, Geometric mean, and Harmonic Mean | AM, GM and HM | #SSC #CDS

Harmonic mean is a type of numerical average that is usually used in situations when the average rate or rate of change needs to be calculated. Harmonic mean is one of the three Pythagorean means. The remaining two are the arithmetic mean and the geometric mean. These three means or averages are very important as they see widespread use in the field of geometry and music.

If we are given a data series or a set of observations then the harmonic mean can be defined as the reciprocal of the average of the reciprocal terms. This implies that the harmonic mean of a particular set of observations is the reciprocal of the arithmetic mean of the reciprocals.

Also Check: Different Kinds Of Lines In Geometry

Hm For Ungrouped Data

Let x1, x2, …, xn be the n observations then the harmonic mean is defined as

Example 5.11

A man travels from Jaipur to Agra by a car and takes 4 hours to cover the whole distance. In the first hour he travels at a speed of 50 km/hr, in the second hour his speed is 64 km/hr, in third hour his speed is 80 km/hr and in the fourth hour he travels at the speed of 55 km/hr. Find the average speed of the motorist.

Solution:

Average speed of the motorist is 60.5km/hr

Real World Applications Of The Geometric Mean

It turns out that there are many practical uses for the geometric mean, as multiplicative-ish relationships abound in the real world.

One canonical example is:

Compound Interest

Assume we have $100,000 that accrues a varying rate of interest each year for 5 years:

annual interest rates: 1%, 9%, 6%, 2%, 15%

Wed like to take a shortcut to find our average annual interest rate, & thus our total amount of money after 5 years, so we try to average these rates:

÷ 5 = .066 = 6.6%

Then we insert this average % into a compound interest formula:

Total interest earned = $100,000 * = $37,653.11Interest + principal = $37,653.11 + 100,000 = $137,653.11Final total = $137,653.11

Just to be sure were not fooling ourselves, lets do this the long way & compare results:

Year 1: 100,000 + = 100,000 * 1.01 = $101,000Year 2: 101,000 * 1.09 = $110,090Year 3: 110,090 * 1.06 = $116,695.40Year 4: 116,695.40 * 1.02 = $119,029.31Year 5: 119,029.31 * 1.15 = $136,883.70Actual final total = $136,883.70

What happened? Our shortcut overestimated our actual earnings by nearly $1,000.

We made a common error: We applied an additive operation to a multiplicative process, & got an inaccurate result.

Now lets try again with the geometric mean:

1.01 * 1.09 * 1.06 * 1.02 * 1.15 = 1.3688370425th root of 1.368837042 = 1.064805657Geometric mean = 1.064805657

Plugging the geometric mean of the interest rates into our compound interest formula:

Thats more like it.

What else is the geometric mean good for?

Harmonic Mean Definition: Formula And Examples

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master’s in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

What Is Harmonic Mean

Which unit represents 100 meters? hectometer kilometer decameter centimeter

The harmonic mean is a measure of central tendency. Say we want to determine a single value that can be used the describe the behavior of data around a central value. Then such a value is known as a measure of central tendency. In statistics, there are three measures of central tendency. These are the mean, median, and mode. The mean can be further classified into arithmetic mean, geometric mean, and harmonic mean.

Section 4 Of : How To Respond To Hm

Offer to lend a supportive ear. If someone sends a message where “HM” means “high maintenance,” they may be looking to talk about a significant other or friend. Do your best to sympathize with them, and ask for more details if they don’t explain the situation right away. For example:

Them: “My girlfriend can be so HM sometimes.”

You: “That’s gotta be frustrating. Did something happen?”

Them: “Yeah. We were picking out a restaurant for dinner.”

How Do You Calculate Hm

It is calculated by dividing the number of observations by the reciprocal of each number in the series. Thus, the harmonic mean is the reciprocal of the arithmetic mean of the reciprocals. The reciprocal of a number n is simply 1 / n.

How do you calculate HM and GM?

The relation between AM GM HM can be represented by the formula AM × HM = GM2.

What two numbers are HM?

Harmonic Mean of two numbers is an average of two numbers. In particular, Let a and b be two given numbers and H be the HM between them a, H, b are in HP. Again, if three terms are in HP, then the middle term is called the Harmonic Mean between the other two, so if a, b, c are in HP, then b is the HM of a and c.

Recommended Reading: What Is Math Models Class In High School

Formula For Harmonic Mean

The general formula for calculating a harmonic mean is:

Harmonic mean = n /

n the number of the values in a dataset
x_i the point in a dataset

The weighted harmonic mean can be calculated using the following formula:

Weighted Harmonic Mean = /

Where:

w_i the weight of the data point
x_i the point in a dataset

Geometric And Harmonic Mean

Arithmetic Mean | Geometric Mean | Harmonic Mean | B.Com (P/H) | Business Statistic

The geometric mean and the harmonic mean forms an important measure of the central tendency of data. They tell us about the central value of the data about which all the set of values of data lies. Suppose we have a huge data set and we want to know about the central tendency of this data set.

We have so many ways by which we can do so. But what if the data sets are fluctuating or we need to add or remove some of the data value? Calculating the average value or the central value will be a tiresome and troublesome task. So, we use geometric and harmonic means as our rescuer.

Also Check: What Is Qc In Chemistry

Relationship Between Arithmetic Mean Geometric Mean And Harmonic Mean

The three means such as arithmetic mean, geometric mean, harmonic means are known as Pythagorean means. The formulas for three different types of means are:

Arithmetic Mean = / n

Harmonic Mean = n /

If G is the geometric mean, H is the harmonic mean, and A is the arithmetic mean, then the relationship between them is given by:

G2 = A.H

The Basics Of A Harmonic Mean

The harmonic mean helps to find multiplicative or divisor relationships between fractions without worrying about common denominators. Harmonic means are often used in averaging things like rates .

The weighted harmonic mean is used in finance to average multiples like the price-earnings ratio because it gives equal weight to each data point. Using a weighted arithmetic mean to average these ratios would give greater weight to high data points than low data points because price-earnings ratios aren’t price-normalized while the earnings are equalized.

The harmonic mean is the weighted harmonic mean, where the weights are equal to 1. The weighted harmonic mean of x1, x2, x3 with the corresponding weights w1, w2, w3 is given as:

\displaystylew_i}\frac}} i=1nxiwii=1nwi

Also Check: What Is The Biological Significance Of Genetic Diversity Between Populations

Harmonic Average Of Two Or Three Numbers

For two positive numbers, x and y, the harmonic mean formula simplifies to the following:

H = 2 * x * y / ,

i.e., you need to double the product of x and y and divide it by the sum of x and y.

For instance, the harmonic mean of x = 2 and y = 8 is equal to:

H = 2 * 2 * 8 / = 32 / 10 = 3.2

For three positive numbers x, y and z we have the following harmonic mean formula:

H = 3 * x * y * z /

As an example, let’s calculate the harmonic mean of x = 2, y = 5, and z = 10:

H = 3 * 2 * 5 * 10 / = 300 / 80 = 15 / 4 = 3.75

Application Of Geometric Mean

If Am & GM of 10 observations are both 15,then value of HM is?

The greatest assumption of the G.M is that data can be really interpreted as a scaling factor. Before that, we have to know when to use the G.M. The answer to this is, it should be only applied to positive values and often used for the set of numbers whose values are exponential in nature and whose values are meant to be multiplied together. This means that there will be no zero value and negative value which we cannot really apply. Geometric mean has a lot of advantages and it is used in many fields. Some of the applications are as follows:

It is used in stock indexes. Because many of the value line indexes which is used by financial departments use G.M.
It is used to calculate the annual return on the portfolio.
It is used in finance to find the average growth rates which are also referred to the compounded annual growth rate.
It is also used in studies like cell division and bacterial growth etc.

Recommended Reading: What Does Scale Drawing Mean In Math

What Is The Abbreviation For Hectometer

Hectometers Length / Distance Conversions. The symbol for hectometer is hm and the International spelling for this unit is hectometre. The base unit for a hectometer is meter and the prefix is hecto. The prefix hecto is derived from the Greek hekaton meaning hundred and is symbolized as h in the Metric System.

Harmonic Mean Of Two Or Three Numbers

Average speed

In many situations involving rates and ratios, the harmonic mean provides the correct average. For instance, if a vehicle travels a certain distance d outbound at a speed x and returns the same distance at a speed y , then its average speed is the harmonic mean of x and y â not the arithmetic mean . The total travel time is the same as if it had traveled the whole distance at that average speed. This can be proven as follows:

Average speed for the entire journey= Total distance traveled/Sum of time for each segment= 1/x+1/y

However, if the vehicle travels for a certain amount of time at a speed x and then the same amount of time at a speed y, then its average speed is the arithmetic mean of x and y, which in the above example is 40 km/h.

Average speed for the entire journey= Total distance traveled/Sum of time for each segment= xt+yt/2t= x+y/2

The same principle applies to more than two segments: given a series of sub-trips at different speeds, if each sub-trip covers the same distance, then the average speed is the harmonic mean of all the sub-trip speeds and if each sub-trip takes the same amount of time, then the average speed is the arithmetic mean of all the sub-trip speeds.

Learn how and when to remove this template message)

Electricity

However, if one connects the resistors in series, then the average resistance is the arithmetic mean of x and y . This principle applies to capacitors in parallel or to inductors in series.