Different Kinds Of Lines In Geometry

Examples Of Curved Lines

A curve is shown in the figure. This is a curve of parabola. The equation of this parabola is y = ax2 where a> 0.

Its general equation is y = ax2 where a0.

If one draws this parabola on a piece of graph paper, some graphs would be too narrow and some would be too wide. It completely depends on the different values of a.

If the values of a increases, the graph gets narrow. On the other hand, if the values of a decreases, the graph gets wide to wider. You can have a check by drawing graph of y = ax2 for different values of a.

If you want to dive deep into general graph, let us go and start the next section.

Consider the general equation of curved line, y = axn where a> 0 and n is even. It represents several graphs depending on the different values of a and n.

What Is A Line

A line has length but no width. A line is a type of geometric figure that can move in both directions. A line is made up of an endless number of points. It is infinite and has no ends on both sides. A line is one dimentional.

In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects having negligible width and depth. It is often described in terms of two points. For example:

A line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation in the concept of analytic geometry whereas, a line may be an independent object, distinct from the set of points which lie on it in the concept of incidence geometry.

Also read:

• 3D Shapes in Real Life

Euclidean Geometry And History Of Non

In about 300 BCE, Euclid penned the Elements, the basic treatise on geometry for almost two thousand years. Euclid starts of the Elements by giving some 23 definitions. After giving the basic definitions he gives us five postulates. The postulates are the assumptions used to define what we now call Euclidean geometry.

The five axioms for Euclidean geometry are:

The fifth postulate is called the parallel postulate. Euclid used a different version of the parallel postulate, and there are several ways one can write the 5th postulate. They are all equivalent and lead to the same geometry.

• “If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.”
• “The sum of the angles in a triangle is exactly 180 degrees.”
• given a line L, and a point P not on that line, there is exactly one line through P which is parallel to L.

Recommended Reading: What Does K Mean In Algebra

Identifying Lines And Angles And Classifying Shapes By Properties Of Lines And Angles

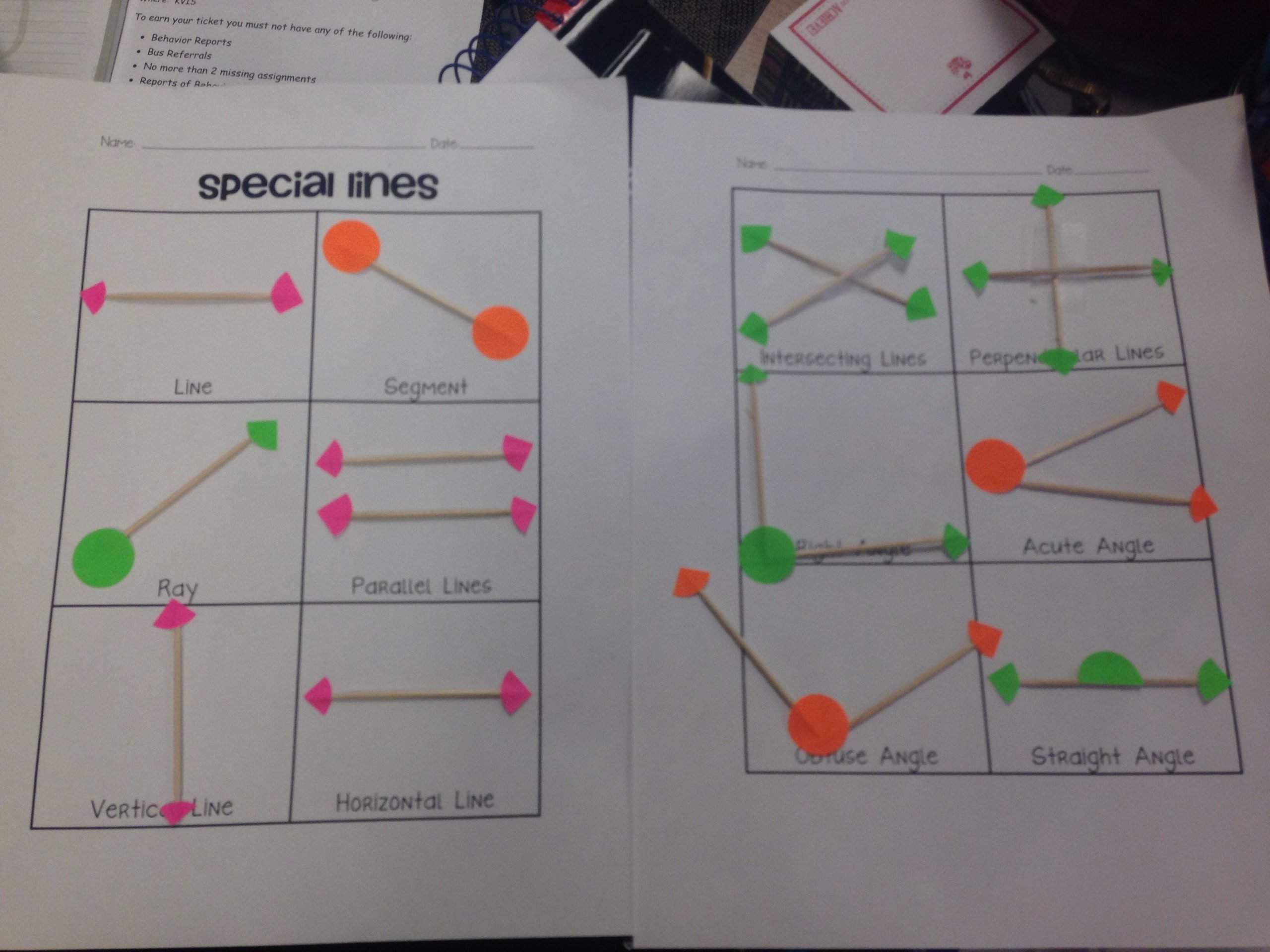
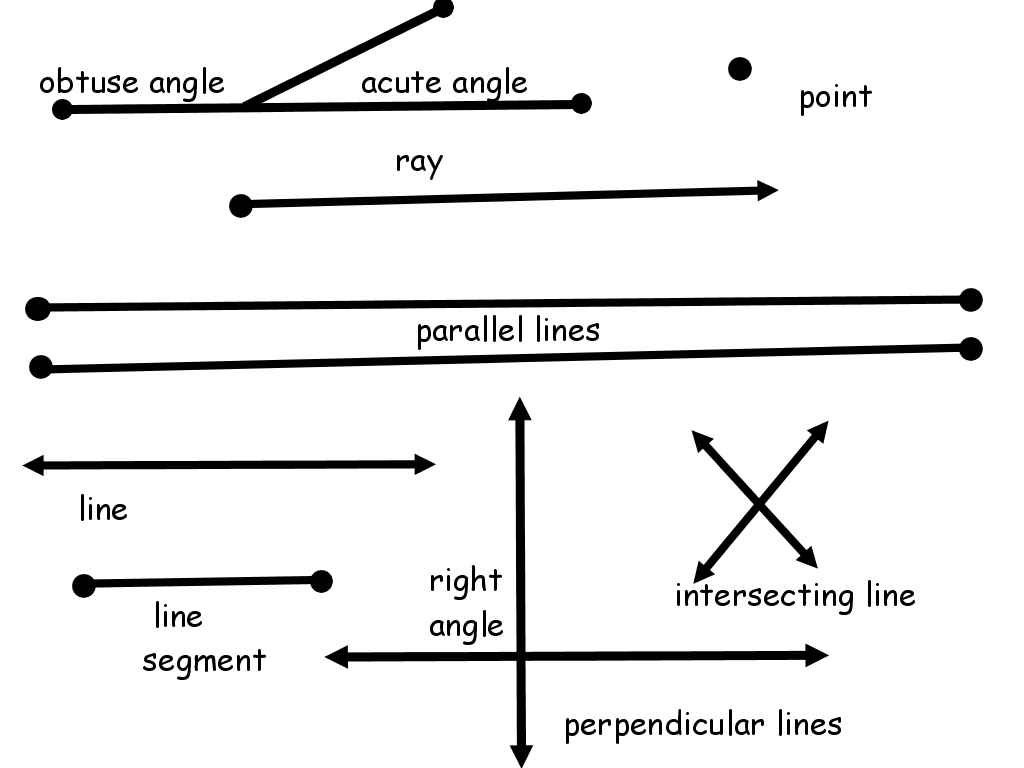
• Identifying line, line segments, and rays: In grade 4, the kids are introduced to geometric objects like line, line segments, and rays. They learn to define geometry lines, line segments, and rays. They also understand the relationship between them. For example, they learn that a ray has one end point and a line segment has two end points. They learn to identify these in two-dimensional figures.

The kids find it easier to understand line segments as they see examples of it in daily life. However, they find the concept of ray and line in geometry little abstract. They also learn geometry symbols for naming geometric line and ray in geometry.

• Understanding Triangles: In grade 4, the kids develop a deeper understanding of the triangle geometry. They get a geometry review of triangles. They learn to classify triangles as equilateral, isosceles, and scalene. They understand that triangle whose all angles or all sides are equal is called an equilateral triangle. A triangle whose exactly two angles or two sides are equal is called an isosceles triangle. A triangle whose no two sides or angles are equal is called scalene triangle.

Lines And Angles Definitions Properties Types Practice Questions

Ancient mathematicians introduced the concept of lines to represent straight objects which had negligible width and depth. Considered as a breadth less length by Euclid, lines form the basis of Euclidean geometry.

When two rays intersect each other in the same plane, they form an angle. The point of intersection is called a vertex.

In this article, we go over the basic properties, definitions, and types of lines and angles related to geometry. Well also look at a few examples for you to understand the properties of lines and angles in a better manner. Before we move forward, take a look at the five-step GMAT Preparation plan to score 700+ on the GMAT:

A line does not have any endpoints. It has an infinite length.

Recommended Reading: What Does Abiotic Mean In Biology

General Curve Of Parabola: Case 1

Let the general equation of parabola be y = axn where a> 0 and n is even. It represents all parabolic graphs of same look but some of them would be wider or narrow. For a> 0, the parabolas are opening to the top.

More precisely, if a = 1 and n = 2, the equation takes the form:y = x2.

Similarly, if a = 2, 3, 4, 5, … and n = 4, 6, 8, 10, … respectively, the equation takes the form:y = 2×4,

General Curve: Case 7

Consider the general equation, x = ayn where a> 0 and n is odd. It generates some equations of graphs for different values of a and n.

Suppose the equation, x = ayn where a> 0 and n is odd. It represents all graphs of same look. For a = 1 and n = 1, it takes the form: x = y.

If you draw x = y, it produces a straight line. But we know a straight line is also a curved line. That is, a straight line is always a curve with curvature zero. This line passes through the origin . And it also goes through …,, , , ,… .

Again, for a = 1 and n = 3, 5, 7, 9, …, the equation x = ayn takes the form:x = y3,

Assume the general equation, x = ayn where a< 0 and n is odd. It represents all graphs of same look. For a = -1 and n = 1 odd, it takes the form: x = -y.

If someone draws x = -y, it renders a straight line that is also a curve. That is, a line is always a curved line. This line passes through the origin . And it also goes through …,, , , ,… .

Again, for a = -1 and n = 3, 5, 7, 9, …, the equation x = ayn takes the form:x = -y3,

One can draw graph of the any equation on the table, all of them look same shapes. Moreover, all the graphs always start from positive x to negative x and from negative y to positive y.

You May Like: What Is The Molecular Geometry Of Ccl4

Line Segments And Rays

There are two kinds of lines: those that have a defined start- and endpoint and those that go on for ever.

Lines that move between two points are called line segments. They start at a specific point, and go to another, the endpoint. They are drawn as a line between two points, as you would probably expect.

The second type of line is called a ray, and these go on forever. They are often drawn as a line starting from a point with an arrow on the other end:

Definition Of A Line Segment

A line segment is a segment of a line, or in other words, we can say that a line segment is a line with two endpoints.

For example, The diagram shows a line L and one segment of this line is AB.

In a plane, there can be many lines or line segments.

And, these lines can be divided into a few types based on the relative positioning of a line with another line.

Recommended Reading: Holt Geometry Lesson 4.5 Practice B Answers

General Curve: Case 6

Let the general equation be y = axn where a< 0 and n is odd. It produces number of equations of graphs depending on the different values of a and n.

Considering the equation, y = axn where a< 0 and n is odd, it represents all graphs of same shape style. For a = -1 and n = 1 odd, it takes the form: y = -x.

If someone draws y = -x, its graph will be a straight line that is also a special cuved line. That is, a straight line, we have previously discussed already, is always a curved line with curvature zero. This straight line passes through the origin . And it also passes through …,, , , ,… .

It goes from positive x to negative x and negative y to positive y.

Again, for a = -1 and n = 3, 5, 7, 9, …, the equation y = axn takes the form:y = -x3

If you draw graph of the any equation on the table, all of them look same shapes. Again, all the graphs always start from positive x to negative x and from negative y to positive y.

General Curve: Case 5

Consider the general equation, y = axn where a> 0 and n is odd. It represents several equations of graphs depending on the different values of a and n.

Suppose the equation, y = axn where a> 0 and n is odd. It gives all graphs of same look. For a = 1 and n = 1, it takes the form: y = x.

If you draw y = x, it will be drawn a straight line that is also a special curved line. That is, a straight line is always a curve with curvature zero. This line passes through the origin . And it also goes through …, , , , , … .

Again, for a = 1 and n = 3, 5, 7, 9, …, the equation y = axn takes the form:y = x3,

If you draw graph of the any equation on the table, all of them look same shapes. Moreover, all the graphs always start from negative x to positive x and from negative y to positive y.

Don’t Miss: Lewis Structure Of Ccl4

What Are Line Segments

Look at the edges of this chessboard.

Each edge is a line segment.

A line segment is a straight path with two endpoints.

A line segment is drawn with points on either end.

Can you measure the length of a line segment?

Yes! You can!

This is because, at a certain point, a line segment ends.

To name a line segment, use its endpoints.

For example, this line segment can be called Line segment AB or Line segment BA.

When writing the name, put a line on top of the label.

Frequently Asked Questions Different Types Of Lines

Q.1. What is a line?Ans: A line is a set of points in a straight path that extends in opposite directions without an end.

Q.2. What are the two types of lines in \- dimensional geometry?Ans:In \-dimensional geometry, the two types of lines are skew lines and coplanar lines.

Q.3. What is a vertical line?Ans:The line that is parallel to \ -axis is called a vertical line.

Q.4. What is a horizontal line?Ans: The line that is parallel to \-axis is called a horizontal line.

Q.5. What are the \ types of lines?Ans: The \ types of lines are horizontal, vertical, parallel, perpendicular, tangent, secant, concurrent, skew, coplanar, oblique, tangent, and intersecting lines.

We hope this detailed article on different types of lines helped you in your studies. If you have any doubts or queries regarding the topic, comment down below and we will be more than happy to help you.

Also Check: Geometry Dash Demon Key Hack

Scale Symmetry And Fractals

Scale symmetry means that if an object is expanded or reduced in size, the new object has the same properties as the original. This is not true of most physical systems, as witness the difference in the shape of the legs of an elephant and a mouse . Similarly, if a soft wax candle were enlarged to the size of a tall tree, it would immediately collapse under its own weight.

A more subtle form of scale symmetry is demonstrated by fractals. As conceived by Benoît Mandelbrot, fractals are a mathematical concept in which the structure of a complex form looks similar at any degree of magnification, well seen in the Mandelbrot set. A coast is an example of a naturally occurring fractal, since it retains similar-appearing complexity at every level from the view of a satellite to a microscopic examination of how the water laps up against individual grains of sand. The branching of trees, which enables small twigs to stand in for full trees in dioramas, is another example.

Because fractals can generate the appearance of patterns in nature, they have a beauty and familiarity not typically seen with mathematically generated functions. Fractals have also found a place in computer-generated movie effects, where their ability to create complex curves with fractal symmetries results in more realistic virtual worlds.

Learn About Lines Line Segments And Rays

Do you know what geometry is?

Geometry is the math of shapes and spaces.

In geometry, we work with different kinds of shapes.

In geometry, we also work with more simple things like points, lines, line segments, and rays.

These are the building blocksof geometry.

In this lesson, let’s learn about each of them.

Don’t Miss: Geometry Segment Addition Postulate Worksheet

Properties Of Parallel Lines

If two lines are intersected by a transversal,pair of acute angles are equal in measure, pairs of obtuse angles are also equal in measure,and any acute angle is supplementary to any obtuse angle.

If line m is || to line n, then:

Alternate interior angles will be equal in measure.

Corresponding angles will be equal in measure.

The sum of degree measures of two interior angles on the same side of the transversal is 180.

Also, the sum of the degree measures by any acute angle and any obtuse angle will be 180.

Some Other Types Of Symmetry

We have different types of symmetries considered depending on the various cases. They are

1.Translational Symmetry

An object or image is moving forward or backward or changing the position from one place to another, but there is no change in the image or object. This type of Symmetry is called Translational Symmetry.

2.Rotational Symmetry

An object or image is rotated in a particular direction but the position of an object or image is identical to the origin of an image or object, then it is called rotational symmetry. It is also called radial symmetry.

From the above figure, we can observe the rotational symmetry. If you rotate the hexagonal object or image in a 60° clockwise direction with respect to the origin, there is no change in the shape of an image. More Examples for Rotational Symmetry are Circle, Hexagonal, Square, Rectangle, and etc

3.Reflexive Symmetry

Reflexive Symmetry is the same as a line of symmetry. Yes, in this type of symmetry one part of the image or object represents the mirror image of another part of the image. Reflexive Symmetry is also called a line of symmetry or mirror symmetry. The below figure is a better example of Reflexive symmetry.

The above object is divide into two parts and the left side part is the mirror image of the right side of the image.

4.Glide Symmetry

It is the combination of both translation symmetry and reflection symmetry.

You May Like: Formal Charge Of Cf4

Points: A Special Case: No Dimensions

A point is a single location in space. It is often represented by a dot on the page, but actually has no real size or shape.

You cannot describe a point in terms of length, width or height, so it is therefore non-dimensional. However, a point may be described by co-ordinates. Co-ordinates do not define anything about the point other than its position in space, in relation to a reference point of known co-ordinates. You will come across point co-ordinates in many applications, such as when you are drawing graphs, or reading maps.

Almost everything in geometry starts with a point, whether its a line, or a complicated three-dimensional shape.

Different Types Of Lines In Geometry Basic Definition And Examples

A line is a one-dimensional geometric figure having length but no width. It is made up of points that are extended in opposite directions infinitely. The different types of lines are horizontal, vertical, parallel, perpendicular, curved, and slanting lines. The definitions of each type of line with an image are given below. Go through the entire article to learn in detail about the Types of Lines in Geometry and examples for each one of them.

Also Check: Prince And Paris Jackson Biological Father

Lines Segments And Rays

Although we all know intuitively what a line is, it is actually difficult to give a good mathematical definition. Roughly, we can say that a line is an infinitely thin, infinitely long collection of points extending in two opposite directions. When we draw lines in geometry, we use an arrow at each end to show that it extends infinitely.

A line can be named either using two points on the line or simply by a letter, usually lowercase .

A line segment has two endpoints. It contains these endpoints and all the points of the line between them. You can measure the length of a segment, but not of a line.

A segment is named by its two endpoints, for example, A ¯ .

A ray is a part of a line that has one endpoint and goes on infinitely in only one direction. You cannot measure the length of a ray.

A ray is named using its endpoint first, and then any other point on the ray (for example, B