Times/ 3 Times/ 4 Times
Question- Maria has 5 packets of gems, and Anderson has 2 times more of Marias packets. How many packets Anderson have?
| Solution- 2 times means we have to multiply Marias packets of Gems with 2, then we get the number of packets Anderson has.No. of Gems packets Maria have= 5No. of Gems packets Anderson have= 2 5=10 |
Conversion Of Units Measurements
Different units are used to measure different quantities. Let us explore the units used to measure the following:
- Length
| inch , feet , yards , miles | |
| Temperature | Kelvin , Fahrenheit , Celsius |
| Area | Square Inch, Square Feet, Acre, Square Yard, Square Mile |
| Volume | Fluid Ounces , pint , quarts , gallons |
| Weight | Ounces, Pounds , Tons |
Non-standard units of measurement are used in the early years of learning, to introduce children to the concept of measuring without them having to read any scales. Reading scales of any kind is a difficult skill in itself, so the idea of non-standard measures is to focus the child on the concept of heavier, lighter, longer, shorter, etc. before they move onto the next step of measuring using standard units.
To measure the length of the objects the non-standard measure used is that of hand spans. Using a handspan to measure objects is an informal way of figuring out the lengths. However, the measurements may vary owing to the subjectivity involved.
Given below is a unit conversion table depicting the relationship between different units.
| Quantity | |
|---|---|
| 1 mile = 1760 yards = 5280 feet = 63,360 inches | |
| Temperature | |
| 1 gallon = 4 quarts = 8 pints = 128 fluid ounces | |
| Weight | 1 ton = 2000 pounds = 32,000 ounces |
Conversions Of Multiple Units
So far you’ve seen examples with only one conversion factor, but this method can be used for more complicated situations. When it’s time to leave for home from your day trip in Mexico, you realize you have just enough gas to make it back across the border into the US before you have to fill up. You notice that you could buy gas for 6.50 pesos per liter before you head home. At first glance that seems more expensive than the $2.87 per gallon at home, but is it really? You need to convert to be sure. Fortunately you came prepared, and looked up the currency exchange rate and volume conversion the morning before you left.
This conversion is more complicated than the previous examples for two reasons. First, imagine that you do not have a single direct conversion factor for the monetary conversion . You know that 1 peso = 8.95 cents, and you also know that 100 cents = 1 dollar. Together, these two facts will let you convert the currency. The second twist is that you are not only changing the money unit you also need to convert the volume unit as well. These two conversions can be done in a single set-up. The order does not matter, but both must be done. Try to set this one up for yourself first, and then run the animation or see the equation below to reveal the solution:
Read Also: Theory Of Everything 2 Song
Base And Derived Units
For most quantities, a unit is absolutely necessary to communicate values of that physical quantity. Imagine you need to buy some rope to tie something onto the roof of a car. How would you tell the salesperson how much rope you need without using some unit of measurement?
However, not all quantities require a unit of their own. Using physical laws, units of quantities can be expressed as combinations of units of other quantities. Therefore, only a small set of units is required. These units are called base units, and other units are derived units. Derived units are a matter of convenience, as they can be expressed in terms of basic units.
Different systems of units are based on different choices of base units. The most widely used system of units is the International System of Units, or SI. There are seven SI base units, and all other SI units can be derived from these base units.
The seven base SI units are:
- Length: m
- Thermodynamic Temperature: K
- Amount of Substance: mol
- Luminous Intensity: cd
The base units of SI are actually not the smallest set possible smaller sets have been defined. For example, there are unit sets in which the electric and magnetic field have the same unit. This is based on physical laws that show that electric and magnetic fields are actually different manifestations of the same phenomenon.
- Area: m2
- Force: \text\cdot\text^2, or the Newton
- Energy: \text\cdot\text, or the Joule
What Are Some Real

-
Suppose an object is moving at 66 ft/sec. How fast would you have to drive a car in order to keep pace with this object?
Content Continues Below
A car’s speedometer doesn’t measure feet per second, so I’ll have to convert to some other measurement. I choose “miles per hour”. I know the following conversions: 1 minute = 60 seconds, 60 minutes = 1 hour, and 5280 feet = 1 mile.
If 1 minute equals 60 seconds , then
Note: The fact that the conversion can be stated in terms of “1”, and that the conversion ratio equals “1” no matter which value or unit is on top, is crucial to the process of cancelling units.
I have a measurment in terms of feet per second I need a measurement in terms of miles per hour. To convert, I start with the given value with its units and set up my conversion ratios so that all undesired units are cancelled out, leaving me in the end with only the units I want.
Affiliate
They gave me something with “seconds” underneath so, in my “60 seconds to 1 minute” conversion factor, I’ll need the “seconds” on top to cancel off with what they gave me. This will leave “minutes” underneath on my conversion factor so, in my “60 minutes to 1 hour” conversion, I’ll need the “minutes” on top to cancel off with the previous factor, forcing the “hour” underneath. Since I want “miles per hour” , things are looking good so far.
Here’s what my conversion set-up looks like:
I would have to drive at 45 miles per hour.
Read Also: What Does Percent Error Mean In Chemistry
What Are Some Examples Of Converting Between Units
-
Convert 3 gallons to quarts.
Quarts are smaller than gallons every gallon has four quarts. Since I’m converting from a larger unit to a smaller unit , my answer needs to be a bigger number. So I multiply:
= 12
-
Convert 7920 yards to miles.
Miles are bigger than yards there are 1760 yards in every mile. Since I’m converting from a smaller unit to a bigger unit , my answer needs to be a smaller number. So I divide:
7920 ÷ 1760 = 4.5
Then:
Answer: 4.5 miles
Note: The above conversions were between two “Imperial” units. Converting between two metric units is so much easier!
The above are examples of one-step conversions between units of the same type namely, Imperial units. To do that type of conversion, you use one conversion factor to convert from the one unit to the other.
Affiliate
But sometimes conversions are more complicated, or you’re not sure which unit is “bigger”. This applies especially in the case of conversions between English and metric units. For instance, which is “bigger”, decaliters or Imperial gallons? Or consider rates: which is “bigger”, 80 miles an hour or 40 meters per second? It’s hard to see how the term “bigger” would apply here.
Unit Conversion And Conversion Factors
A unit conversion expresses the same property as a different unit of measurement. For instance, time can be expressed in minutes instead of hours, while distance can be converted from miles to kilometers, or feet, or any other measure of length. Often measurements are given in one set of units, such as feet, but are needed in different units, such as chains. A conversion factor is a numeric expression that enables feet to be changed to chains as an equal exchange.
Javier constructed 41 chains of dozer line.Notice that Table 2.2 has two conversions for each set of units. When setting up the cancellation table, it is not important which conversion factor is used. What is important is that the appropriate units cancel so that the correct end result is achieved.
Recommended Reading: Holt Geometry Chapter 7 Test Form B Answers
How To Solve Mass Conversion Problems
- Category:
- Learning Resources, Measurement & Data
In todays post, we are going to see some examples of mass conversion problems with different units of mass and we will look at how to solve them.
Remember that previously, we have seen how to solve conversion problems with distance measures. Before beginning with the conversion problems with mass measures, you should review the principle mass measures by visiting the following post: Mass Measurement Problems
Lets begin! First, take notice of the scale of the main units of mass measurement. You will be able to use them to help you with the conversions.
How To Calculate How Much Protein Powder You Need Daily
Nurses need to know how to convert measurements to administer medications and fluids. A physician orders medication with the dose written in milligrams , for example. To administer the medication you must draw it up in a syringe. But syringes aren’t marked in milligrams. You must convert the milligram dose to an amount that you can measure in a syringe, measuring cup or other device, such as a milliliter or cubic centimeter.
Don’t Miss: Is Paris Jackson Michael Jacksons Biological Daughter
How Do You Do Complicated Conversions Like Between Metric And Imperial
For these sorts of conversion, we use as many conversion factors as we need, setting up a long multiplication so the units we don’t want cancel out. Note: I’m not talking here about numbers “cancelling out”, like when you’re multiplying fractions. Instead, I’m talking about treating the units as though they were numbers, and cancelling them.
How To Pick A 1
You might be wondering how I knew to pick that particular fractionthat was equal to 1. There are just two simple steps:
Find a conversion factor between the given units and thedesired units, and write it as an equation.
Example: whether you have miles and need kilometers, oryou have kilometers and need miles, you can use eitherconversion factor between miles and kilometers, namely1 mi = 1.61 km or 1 km = 0.621 mi.Either equation will work equally well.
Convert that equation to a fraction with thedesired units on top and the given units on the bottom.More formally, divide both sides by the value of the side thatcontains the given units.
Example: To convert from miles to kilometers, you need afraction with the desired units on top and the givenunits on the bottom. Based on the above conversion factors, thatfraction must be either
1.61 km 1 km ------- or -------- 1 mi 0.621 mi
Those fractions look different, but remember that theyre bothequal to 1 and therefore they are just different forms of the samefraction. Either one will work just fine for the conversion.
Once youve selected a useful fractional form of 1, multiply theoriginal measurement by the fraction, and simplify.
Example: If the original measure was 15.7 miles, you wouldmultiply by either of the above fractions and obtain 25.3 km.
Recommended Reading: Draw The Lewis Structure For Ccl4.
Useful Tricks To Solve Math Problems Easily
Does your child always struggle with problem sums?
Is your child always leaving them blank, not knowing how to start solving them?
Or does he have problems expressing the problem in the right mathematical statements?
Many parents thought that their child may have problems understanding the question.
However, the underlying problem is deeper than that.
If you think about it, the language used in Primary School Math are not that tough.
We dont see bombastic words or fancy phrases.
Instead, we usually see straightforward statements like:
John has 20 more apples than Mary,
He gave 1/2 of his apples to Mary,
They had equal number of fruits in the end etc
If your child read the question slowly and carefully, he will probably knows what the question mean.
But
Example : Miles Per Second To Miles Per Hour
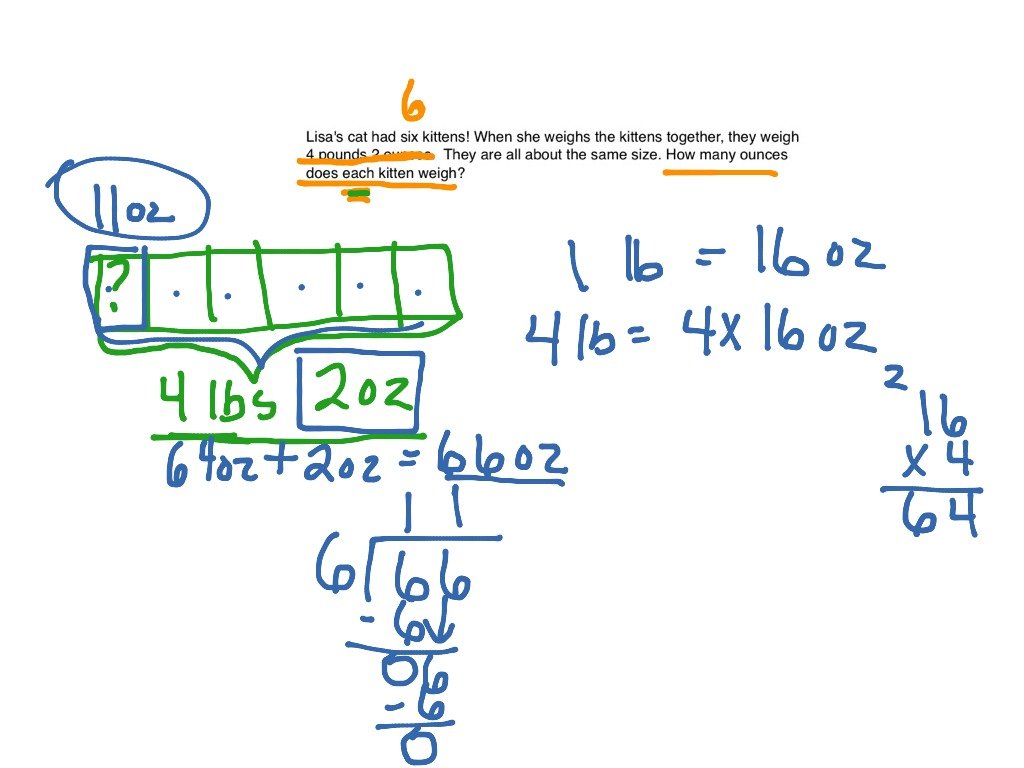
Escape velocity from the earths surface is about 7.0 mi/sec. What isthat in mi/hr?
| Here again, youre converting only one unit, seconds to hours , and the miles per is just along for the ride. But whats different here is that the units youre converting are in the denominator of the fraction, not in the numerator. Look what happens if you apply the old rule of desired units on the top: |
7.0 mi 1 hr------ × -------- sec 3600 sec |
| and you end up with |
7.0 mi hr------------3600 sec sec |
This is no good: you cant simplify this fraction to remove theseconds . Rule 2 in picking a fraction, asoriginally stated, only applied when the units to be converted were inthe top of the fraction .
Heres the more general form of Rule 2,the form that will always work:when picking your fraction that equals 1,put the given units in the opposite position from where they are in the originalmeasurement. If the original measurement had the given units on thetop, your 1-fraction will have them on the bottom but if the givenunits are on the bottom of the original measurement then your1-fraction must have them in the top. Do this so that you can dividetop and bottom by the given units when simplifying.
Lets come back to the example, 7.0 mi/secconverted to mi/hr, and do it the right way:
| Write the conversion equation: |
about 25,000 mi/hr |
Don’t Miss: John Thomas Brother Of Beth Thomas
Example : Square Feet To Square Meters
Sometimes you have to deal with squared units. In the US, you oftensee them with a sq prefix. But they are actually easier tomanipulate if you treat them just like variables and use the² sign.
I correspond with a friend outside the US, and we are describingour homes to each other. If my apartment measures 850 square feet, whatis that in square meters? In other words, convert 850 ft² tom².
Solution: I need a fraction equal to 1, with m² on the top andft² on the bottom. The way to obtain that is to form a fractionequal to 1 with plain m on the top and plain ft on the bottom, andthen square it .
| As it happens, I dont remember the conversion from feet to meters, but I do remember the conversions between both of them and inches: |
1 ft = 12.00 in1 m = 39.37 in |
| So I construct my fraction in two steps: |
1 = 1 × 1 1 m 12.00 in1 = -------- × -------- 39.37 in 1 ft 12.00 m1 = -------- 39.37 ft 0.3048 m1 = -------- ft |
| Now remember that the original measurement is in ft². Therefore I must multiply the original measurement, 850 ft², by the square of the above fraction, to get ft² in the denominator and match the ft² in the original measurement: |
²850 ft² × |
| When a fraction is squared, thats the same as squaring the top and squaring the bottom, including units: |
850 × 0.3048² ft² m² -------------------- ft² |
| Divide through by ft² top and bottom, and do the arithmetic to get the answer: |
850 ft² = 79 m² |
But My Calculator Has A Convert Key
So? sooner or later youll have to convert a measurement withunits that arent in your calculator. At that point a lot of studentsstart to guess, and the more complex the units the more likely theyllguess wrong. If you understand what youre doing, using the techniqueson this page, youll have smooth sailing.
You can also use these same techniques to do currency conversions,which are probably not on your calculator because the rates fluctuate.See the practice problems.
Don’t Miss: Geometry Mcdougal Littell Answers
Is This Really Multiplying By 1
But wait a minute! I hear you say. Youstarted with 4.5 and ended up with 270. How is that multiplying by 1?The answer is that we didnt start with a dimensionless pure number4.5, but with 4.5 hours and we didnt end up with a pure number 270but with 270 minutes. You should be able to convince yourself that ifyou bake a turkey for 270 minutes or 4½ hours, either way youwait the same length of time for dinner.
A number with units is different from a numberwithout units or with different units, just as 8x is differentfrom both 8 and 8y. Think of it this way: 3.27 dollars or eurosis the same as 327 cents, when you multiply by the carefully chosenform of 1, 100 cents/dollar or 100 cents/euro. If the top and bottomof the fraction are equal, the fraction equals 1 and the value aftermultiplying is the same as the value before multiplyingbutexpressed in different units, which of course is the whole point.
You might be asking yourself, Why all the fuss?Anybody knows that to convert hours to minutes you have to multiply by60. Well, yes, thats true. But I deliberately chose a simple exampleto show the method. Ill try to use more realistic examples from here on.
Converting Units Of Measure In The Same System
Imagine you are catering for a party and go to the wholesale shop to buy flour. You need 200 g of flour for each batch of cookies you will be making and need to make 30 batches. You can buy a 5 kg bag of flour but arent sure if that will be enough.
In order to work out if you have enough flour, you need both measurements to be in the same unit kg or g before you can do the calculation. For units of measure that are in the same system its a simple process to convert one measurement into another.
For now we will focus on what is known as the metric system of measurement . In most cases, if you want to convert between units in the metric system you will just need to multiply or divide by 10, 100 or 1000.
Take a look at the diagrams below which explain how to convert each type of measurement unit.
Recommended Reading: Ccl4 Geometry