What Is The Definition Of Point In Geometry

Bounds On Standard Deviation

For a set of N> 4 data spanning a range of values R, an upper bound on the standard deviation s is given by s = 0.6R.An estimate of the standard deviation for N> 100 data taken to be approximately normal follows from the heuristic that 95% of the area under the normal curve lies roughly two standard deviations to either side of the mean, so that, with 95% probability the total range of values R represents four standard deviations so that s R/4. This so-called range rule is useful in sample size estimation, as the range of possible values is easier to estimate than the standard deviation. Other divisors K of the range such that s R/K are available for other values of N and for non-normal distributions.

Standard Deviation Of Average Height For Adult Men

If the population of interest is approximately normally distributed, the standard deviation provides information on the proportion of observations above or below certain values. For example, the average height for adult men in the United States is about 70 inches, with a standard deviation of around 3 inches. This means that most men have a height within 3 inches of the mean one standard deviation and almost all men have a height within 6 inches of the mean two standard deviations. If the standard deviation were zero, then all men would be exactly 70 inches tall. If the standard deviation were 20 inches, then men would have much more variable heights, with a typical range of about 5090 inches. Three standard deviations account for 99.73% of the sample population being studied, assuming the distribution is normal or bell-shaped .

Point Masses And The Dirac Delta Function

Often in physics and mathematics, it is useful to think of a point as having non-zero mass or charge . The Dirac delta function, or function, is a generalized function on the real number line that is zero everywhere except at zero, with an integral of one over the entire real line. The delta function is sometimes thought of as an infinitely high, infinitely thin spike at the origin, with total area one under the spike, and physically represents an idealized point mass or point charge. It was introduced by theoretical physicist Paul Dirac. In the context of signal processing it is often referred to as the unit impulse symbol . Its discrete analog is the Kronecker delta function which is usually defined on a finite domain and takes values 0 and 1.

Also Check: What Is Physics In High School

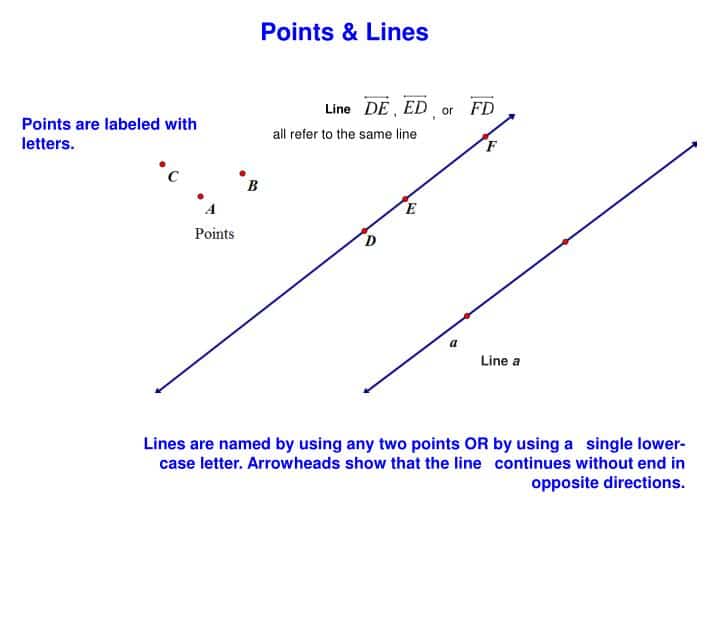
Line Segments And Rays

A line segment, or segment, is a part of a line and contains two endpoints and all points between them. Whereas a ray consists of one endpoint, or initial point, and extends in only one direction. When writing lines, planes, or segments, the order of each point is not important but when naming rays we must always list the endpoint first.

Line Segments in Geometry

Rays in Geometry

Together we will look at the theory behind these terms and accurately identify and represent them all while working through countless examples.

Collinear Points In Real Life

Anytime you have a series of individual items in a single straight line, you have models of collinear points. Suppose you have eggs in a carton each egg in one row is a collinear point:

Students seated at a long cafeteria table are collinear. Football players on the line of scrimmage are collinear. Rings on a shower curtain, plants in one row in a garden, numbers on a ruler, moviegoers in a ticket line, and commuters seated on a train are collinear.

For real-life examples to be good models of collinear points, you need to be able to draw a straight line through them. Think of the individual kernels on one row of an ear of corn.

Also Check: What Is Po4 In Chemistry

Complete Rejection Of The False Grammatical Account: Geometric Points Are Not Names Of Objects

But the word ‘point’ is not used in geometry to name anything. A point is not a “geometric object” it is not an “atomic dot”. There are no objects in geometry. A point is a location a ‘geometric point’ is a point of reference. That is the grammar of the word.

A point is a location in space. Or in plane geometry: a point is a location in the plane. That is the best general definition of the word ‘point’ as it is used in geometry that I can think of: However, that definition is not by itself the clearest definition for it does not specify everything it should.

A point is an address. In Euclidean geometry, “a point is a relation” — a relation to what? To other points in the plane. That is, when we say that ‘point’ = ‘an address in the plane’, that address look like this: ABC — i.e. the address of point B is given relative to points A and C. It is possible to begin a proof: “Let A be a point of line n”, because that too states a relationship .

By the word ‘point’ we mean ‘a unique location in the plane’. How is that location determined? Relative to other locations. Is that circular? Only in the sense that every system of assigning addresses begins with an arbitrarily assigned point of reference — and there must be other points in the system.

What Does A Parallelogram Look Like

Take a rectangle and push either its left or ride side so it leans over you have a parallelogram. A rectangle is a type of parallelogram.

You can draw parallelograms. Use a straightedge to draw a horizontal line segment, then draw another identical line segment some distance above and to one side of the first one, so they do not line up vertically.

Make sure that second line segment is parallel to the first line segment. Connect the endpoints, and you have a parallelogram!

Read Also: What Is 9th Grade Math

Three Undefined Terms: Point Line And Plane

Univ. of WisconsinJ.D. Univ. of Wisconsin Law school

Brian was a geometry teacher through the Teach for America program and started the geometry program at his school

In Geometry, we have several undefined terms: point, line and plane. From these three undefined terms, all other terms in Geometry can be defined. In Geometry, we define a point as a location and no size. A line is defined as something that extends infinitely in either direction but has no width and is one dimensional while a plane extends infinitely in two dimensions.

Types Of Points And Lines

There are different types of points in geometry. Let us discuss them to identify them easily.

Collinear Points and Non-Collinear PointsIf three or more points lie on a single straight line then the points are called collinear points. If the group of points do not lie on the same line then those points are called non-collinear points.Coplanar Points and Non-Coplanar PointsIf a group of points lie on the same plane then they are said to be coplanar points. A set of points that do not lie on the same plane are non-coplanar points.Observe the following figure which shows the different types of points.

Recommended Reading: What Are The Five Subfields Of Geography

Philosophy Of Mathematics Is The View From Outside Mathematics: What We Imagine About Points Is Of No Importance To Geometry

When I began to teach myself geometry — as any child might do — I used the form of expression ‘Place a point P on line n such that …’ rather than ‘Choose a point P on line n such that …’ — What is remarkable is that this did not matter in the least: it did not affect my proofs.

‘Place a point’ and ‘Choose a point’ can be used interchangeably with no harm done. Use any form of expression you like as long as you don’t break the rules of the game or ask for nonsense .

This is an important method of proof: ‘If p, then q but not-q. Therefore not-p.’ We use this e.g. to prove that two lines have no more than one point in common — by assuming that they have two points in common. But we do not break the rules of the game to do this that is the difference between a postulate and a theorem: we can propose any theorem we like without changing the rules of the game. A theorem is proved or disproved, but we do not prove the contrary of a postulate we simply discard it .

Go ahead! talk about points as though ‘point’ were the name of an invisible object. It does no harm.

Philosophy of Mathematics is the view from outside it is the understanding of the calculus that is not needed for calculating. “What is mathematics?” is not a mathematical question. And mathematicians can dismiss it as a “matter of opinion”, something to chat about.

No theorem necessarily has an application outside geometry

Corrected Sample Standard Deviation

If the biased sample variance is used to compute an estimate of the population’s standard deviation, the result is

s

2 , }=}\gamma _}}\sum _^\left^}},}

where 2 denotes the population excess kurtosis. The excess kurtosis may be either known beforehand for certain distributions, or estimated from the data.

Read Also: How To Find Dipole Moment Physics

What Is The Definition Of A Mathematical Point

A point is defined in the elements as that which have no parts, but what does this mean? There is nothing in the physical world that doesn’t have an extension. You can’t say a point is primitive notion because primitive notions are for objects which fall under our senses but mathematical points don’t. So how to define a mathematical point?

The brief answer: It depends on the context. Different areas of mathematics use the notion of a point. Here is a small sample:

Uncorrected Sample Standard Deviation

The formula for the population standard deviation can be applied to the sample, using the size of the sample as the size of the population . This estimator, denoted by sN, is known as the uncorrected sample standard deviation, or sometimes the standard deviation of the sample , and is defined as follows:

,\,x_,\,\ldots ,\,x_\}} are the observed values of the sample items, and x ¯ }} is the mean value of these observations, while the denominator N stands for the size of the sample: this is the square root of the sample variance, which is the average of the squared deviations about the sample mean.

This is a consistent estimator , and is the maximum-likelihood estimate when the population is normally distributed. However, this is a biased estimator, as the estimates are generally too low. The bias decreases as sample size grows, dropping off as 1/N, and thus is most significant for small or moderate sample sizes for N 75 the bias is below 1%. Thus for very large sample sizes, the uncorrected sample standard deviation is generally acceptable. This estimator also has a uniformly smaller mean squared error than the corrected sample standard deviation.

Also Check: Who Wrote Psychology And Industrial Efficiency

A Line Segment And A Ray

A line segment is a line that has two definite endpoints. If a line segment has two endpoints A and B, then it is denoted by AB bar.

A ray is a line that starts from a point and extends indefinitely in a direction. It has only one endpoint.

An example of a ray is a torch light that starts from an end and goes endlessly in one direction.

We Know The Word’s Meaning Until We Are Asked To Explain It

We know how to use the word ‘point’ well enough until we are called to give an account of it . Because we try to give the wrong type of account. Rather than try to describe the use of a word as we know it, we try to explain “what a point is” — i.e. to theorize about an invisible object. We become like a philosopher gesticulating with the sign ‘I know’ . We say ‘A point is …’ while the meaning of these words “seems to float before our eyes” and we want to point to that as proof positive that we understand what we are saying. But the logic of our language does not work that way.

That we now have ways to describe — i.e. to remind ourselves of — the use of a word shows the value of Wittgenstein’s work.

But if it is simply grammar that excludes ‘name of an ideal object’ as a part of speech, then why not make just this rule: to allow it as a part of speech? But is there any need for that? It already is a part of speech — in fairy tales.

Suppose we made this rule: that by ‘point’ we mean an invisible object. But does just uttering that rule accomplish anything? It gives us a picture with one hand , and then erases it with the other this is an example of grammar stripping. Does it give us a picture at all?

But is the grammar of ‘point’ like the grammar of ‘elf’ — is this a helpful comparison? Is this a useful grammatical set: ?

Don’t Miss: What Does Hc Stand For In Chemistry

What Is A Point Is A Question That Belongs To The Philosophy Of Geometry

But what right have I to talk about geometry if I have studied no more than plane geometry? — As if knowing more geometry would throw light on its use of the word ‘point’!

The question of “what a point is” is a question, not of geometry, but of philosophy .

We must try to approach the question from all possible points of view, in order to free ourselves from the charm of any particular one of them.

“It is high time we compare these phenomena to something different” — one may say. — I am thinking e.g. of mental illnesses.

I am thinking of mathematical signs we always compare this language to name-of-object language.

Reality is number, which is both its stuff and form

From one point of view, the stuff of reality is always changing its form. From another point of view, what changes is not the form of reality but its stuff. But from the Pythagorean point of view, this is a distinction without a difference: reality is number:

The Pythagoreans defined ‘point’ as: a unit with position. But the combination of words ‘a unit with position’ is nonsense unless there is more than one unit — i.e. position is relative or, in other words, a relation among points. A ‘figure’ is a ‘constellation of points’. And the word ‘unit’ indicates that a point’s location in the constellation must be unique. This is where geometry begins: A point is that without parts, two points define a line, three points not all in one line define a plane. This is Euclid.

The Forms as non-mathematical-numbers

Diagonals Of A Parallelogram

Start at any vertex . Write a capital letter, then move either clockwise or counterclockwise to the next vertex. Use a different capital letter. For our parallelogram, we will label it WXYZ, but you can use any four letters as long as they are not the same as each other.

The four line segments making up the parallelogram are WX, XY, YZ, and ZW. Notice that line segments WX and YZ are congruent. Line segments XY and ZW are also congruent.

The interior angles are W, X, Y, and Z. The opposite angles are congruent. In our parallelogram, that means W = Y and X = Z.

Connecting opposite vertices gives you diagonals WY and XZ. One interesting property of a parallelogram is that its two diagonals bisect each other . Another property is that each diagonal forms two congruent triangles inside the parallelogram.

Recommended Reading: How Hard Is The Ut Math Assessment

Definition Of Population Values

Let be the expected value of random variableX with density f:

X

Using words, the standard deviation is the square root of the variance of X.

The standard deviation of a probability distribution is the same as that of a random variable having that distribution.

Not all random variables have a standard deviation. If the distribution has fat tails going out to infinity, the standard deviation might not exist, because the integral might not converge. The normal distribution has tails going out to infinity, but its mean and standard deviation do exist, because the tails diminish quickly enough. The Pareto distribution with parameter ] has a mean, but not a standard deviation . The Cauchy distribution has neither a mean nor a standard deviation.

Points Lines And Shapes

Definitionof points, lines and shapes in geometry:

Point: A point is the fundamental element of geometry. If we put the tip of a pencil on a paper and press it lightly, we see a very small mark on the paper. This mark is known as a point.

The smallest mark denotes the existence of a point. We say that a point does not have any length, breadth or thickness, but it has a definite position.

It can be named by a capital letter of the English alphabet like A, B, C, . etc.

In short, we can make a small dot on a paper by using a sharp pencilor a tip of the needle. It is called a point. It represents a position and ismarked by a capital letter A, B, C etc. A point has no size or shape. So, on aline an infinite number of points exist.

Line: If two pointsare made at a distance on a surface and are joined by a pencil then a part of aline is formed. The part of the line will be straight if the surface is planeand curved if the surface is curved.

Thus, if we join any two points with a ruler and extend iton both sides, a line is formed.

A line is indicated by drawing arrow-heads on both sides ofthe part of a line.

The arrow-heads at the ends indicate that the line goes onin both directions. A line has no end, so it has not a definite length.

The name of a line is indicated by two capital letters ofthe English alphabet.

The symbol is placed over the letters as AB, CD.

Recommended Reading: What Is Br In Chemistry