Corrosionpedia Explains Tension Force
Tension force is one of the most common forces. For this, many materials are specified by what is known as their tensile strength. The tensile strength helps designers understand the amount of tension force a material would be able to withstand. From what is known as the yield tensile strength, the amount of tension force that would cause a material to plastically deform can be calculated. From the ultimate tensile strength, the tension force at which a material failure would occur can be calculated.
Tension forces are encountered in many different applications. One example of a tension force is a seat belt clip in a car upon impact. The seat belt clip must be able to withstand the force of a body being propelled forward during a traffic accident. Another example is a less acute instance of a tension force occurs in a suspension bridge that constantly undergoes the onboarding and offloading of cars. If the cable material does not have an adequate tensile strength, then a bridge failure could occur.There is no one formula to calculate the tension force in all circumstances. Often, Newton’s second law is used to calculate the normal force:Every physical object that is in contact with another object exerts some type of force on it and vice versa. The contact forces are referred to by different terms based on the nature of objects. If one of the forces in question that is the exerting object is a rope, cable or chain, it is referred to as tension.
Causes Of Surface Tension
Various intermolecular forces, such as Van der Waals forces, draw the liquid particles together. Along the surface, the particles are pulled toward the rest of the liquid, as shown in the picture to the right.
Surface tension is defined as the ratio of the surface force F to the length d along which the force acts:
gamma=F / d
Units of Surface Tension
Surface tension is measured in SI units of N/m , although the more common unit is the cgs unit dyn/cm .
In order to consider the thermodynamics of the situation, it is sometimes useful to consider it in terms of work per unit area. The SI unit, in that case, is the J/m2 . The cgs unit is erg/cm2.
These forces bind the surface particles together. Though this binding is weak – it’s pretty easy to break the surface of a liquid after all – it does manifest in many ways.
Some Phenomena Based On Surface Tension
1. Medicines used for washing wounds, as dettol, have a surface tension lower than water.
2. Hot soup is more tasteful than the cold one because the surface tension of the hot soup is less than that of the cold and so it spreads over a larger area of the tongue.
3. Insects and mosquitoes swim on the surface of water in ponds and lakes due to surface tension. If kerosene oil is sprayed on the water surface, the surface tension of water is lowered and the insects and mosquitoes sink in water and are dead.
4. If we deform a liquid drop by pushing it slightly, then due to surface tension it again becomes spherical.
5. The detergents are used for cleaning the dirty clothes. The molecule of detergent can attached with water and dirt molecules and they take away the dirt with them, when we wash the clothes with detergent.
Surface Tension:In Physics, the tension of the surface film of a liquid because of the attraction of the surface particles by the bulk of the liquid, which tries to minimize surface area is called surface tension. When the surface of the liquid is strong enough, then surface tension is applicable. It is strong enough to hold weight.
Read Also: Climate Of The New England Colonies
How Can We Find The Direction Of The Tension Force
The direction of tension is the pull which is given the name tension. Thus, the tension will point away from the mass in the direction of the string/rope. In case of the hanging mass, the string pulls it upwards, so the string/rope exerts an upper force on the mass and the tension will be in the upper side.
In What Cases Would The Force Of Tension Between Two Bodies Connected By The Same Rope Differ
The rope acts as a transferring agent of the force, so there should never be a scenario in which two objects connected by one rope experience tension forces of different magnitudes.
Stay tuned to BYJUS and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Also Check: College Algebra Hawkes
Terms Which Are Critical In Relation To The Tension
Surface Tension:
Surface tension is the inclination of liquid surfaces to contract into the minimum surface zone conceivable. Surface tension permits insects like water striders and other such insects, normally denser than water, to buoy and slide on a water surface.
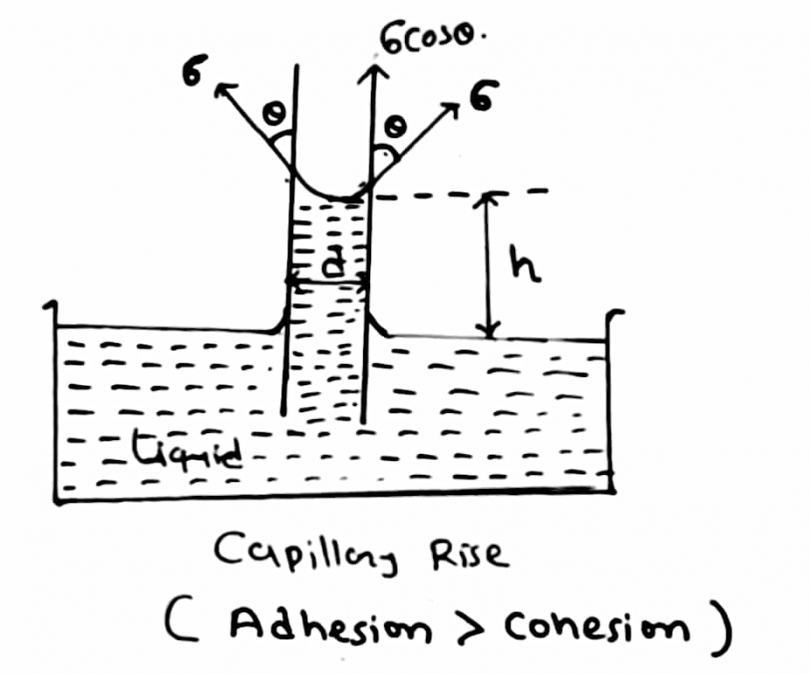
At liquid-air interfaces, surface tension results from the more noteworthy fascination of fluid particles to one another than to the atoms noticeable all around . The net impact is an internal force at its surface that makes the fluid carries on as though its surface which was secured with an extended flexible layer. Along these lines, the surface goes under tension from the imbalanced forces, which is most likely where the expression “surface tension” originated from. As a result of the moderately high fascination of water particles to one another through a network of the hydrogen bond, water has a higher surface tension than most of the other fluids. Surface tension is a critical factor in the marvel of capillarity. Surface tension has the component of force per unit length, or of energy per unit area. These two are comparable, however when alluding to energy per unit of the region, usually to utilize the term surface energy, which is a progressively broad term as it applies likewise to solids. In Physics, surface tension is utilized for either surface tension or surface energy.
Tensile Strength:
Quarters In A Full Glass Of Water
Needed materials:
- 10 to 12 Quarters
- glass full of water
Slowly, and with a steady hand, bring the quarters one at a time to the center of the glass. Place the narrow edge of the quarter in the water and let go.
As you continue with more quarters, you will be astonished how convex the water becomes on top of the glass without overflowing!
Possible Variant: Perform this experiment with identical glasses, but use different types of coins in each glass. Use the results of how many can go in to determine a ratio of the volumes of different coins.
Recommended Reading: Lesson 4.5 Practice B
Example 1 Weight On An Incline A Two
Consider the skier on a slope shown in Figure 2. Her mass including equipment is 60.0 kg. What is her acceleration if friction is negligible? What is her acceleration if friction is known to be 45.0 N?
Figure 2. Since motion and friction are parallel to the slope, it is most convenient to project all forces onto a coordinate system where one axis is parallel to the slope and the other is perpendicular . N is perpendicular to the slope and f is parallel to the slope, but w has components along both axes, namely w and \textbf_. N is equal in magnitude to w, so that there is no motion perpendicular to the slope, but f is less than w, so that there is a downslope acceleration .
Strategy
Solution
The magnitude of the component of the weight parallel to the slope is _= \sin = mg\sin , and the magnitude of the component of the weight perpendicular to the slope is _=\cos = mg\cos.
Neglecting friction. Since the acceleration is parallel to the slope, we need only consider forces parallel to the slope. The forces parallel to the slope are the amount of the skiers weight parallel to the slope w and friction f. Using Newtons second law, with subscripts to denote quantities parallel to the slope,
_=\frac_\parallel }}
where _\parallel}=_=mg\sin, assuming no friction for this part, so that
is the acceleration.
_\parallel }=_-f
and substituting this into Newtons second law, _=\frac_\parallel }}, gives
_=\frac_\parallel}}=\frac_-f}=\frac\sin-f}.
We substitute known values to obtain
What Is Surface Tension In Physics
Surface Tension:Surface tension is the property of any liquid by virtue of which it tries to minimise its free surface area.
Surface tension of a liquid is measured as the force acting per unit length on an imaginary line drawn tangentially on the free surface of the liquid.
We are giving a detailed and clear sheet on all Physics Notes that are very useful to understand the Basic Physics Concepts.
Also Check: Paraguay Geography Features
Determining Tension On A Single Strand
The Tension In One Dimension:
In one dimension string,the tension is a scalar quantity. The tension is not negative. When the tension is zero, the string is loose. Unlike ropes and strings,which have a dimension of length yet no cross-section, ropes and strings are massless. Since the tension is constant along the string, there will be no bends not caused by vibrations and pulleys, as they occur with vibrations and pulleys.
According to Newton’s third law, these are the forces applied on the ends of the string or rope by the objects to which the ends are attached. When a string vibrates, the frequencies it produces are determined by its tension. These frequencies are derived from Newton’s law of motion.
Read Also: Is Michael Jackson Biological Father
What Is Tension Force
Imagine that you pick up a basketball from the ground. You would feel the ball’s weight in your hands because of the force of gravity acting on the ball’s mass. Now imagine tying a rope around the ball, which you then use to lift the ball again. You would still feel the ball’s weight through the rope. In this situation, the rope is now in tension. What keeps the rope together is called the tension force. Cutting the rope will release the tension force and would put the ball in free fall.
Tension force is an axial force that passes through an object that pulls, like a rope, string, or chain. We can also observe tension force in other materials, like rods and bars, given that they are subjected to external pulling or tensile loads. Materials with high tensile strength make the best rods and bars as they don’t break easily when subjected to tension forces. You can check our stress-strain calculator which discusses about elasticity to learn more about tensile strength.
Tension force is also a great example of Newton’s Third Law of Motion. Newton’s Third Law of Motion states that when a body exerts a force on a second body, the second body exerts an equal force in the opposite direction back onto the original body. Tension force is a reactive force that counteracts an external pulling force. This characteristic of tension force is the reason why it is, in a way, quite similar to normal force, which you can learn more about by visiting our normal force calculator.
Newton’s Laws And Tension Force:
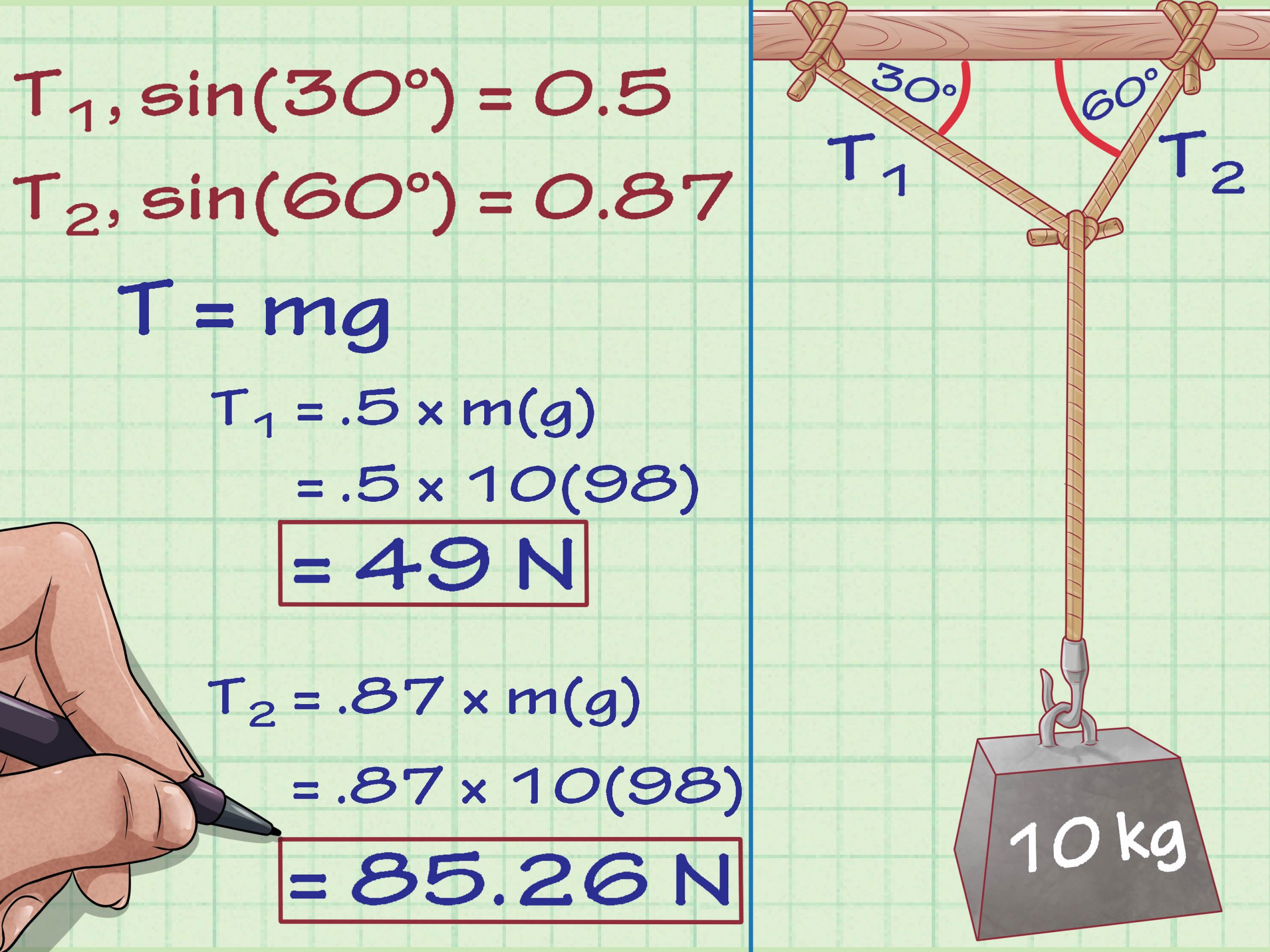
Newton’s law is applied to tension in the final application. Cables and rope are usually used to transmit force, which causes tension. For example, let’s consider a rope pulling a block. People pulling at one end of the rope cannot exert direct force on the block at the other end as they are not in contact with the block. So the rope exerts a force on the block which is transmitted to the block by the rope. An object experiencing tension force is a block.
Massless ropes or cables are the basis of classical mechanics. A massless cable or rope transmits force equally from one end to the other. By using the massless rope as an example, a person pulling a massless rope with the force 30 N then the pull experienced by the block will be the same 30 N.
The total force on a massless rope should always be zero. This can be proven using Newtons second law. The mass of a massless rope equals the force acting upon it, so a net force on a rope causes infinite acceleration A=F/m and zero mass.
It is physically impossible to experience the net force in the situation described above, so the massless rope cannot experience it.
Consequently, all of the massless ropes will undergo equal and opposite tension forces. When a man pulls a block with a rope, the rope experiences tension from the pull in one direction, and tension from the reactive force of the block in the opposite direction.
Don’t Miss: Segment Addition Postulate And Midpoint Worksheet
Definition Based On Work And Energy
In order to attract a molecule from the interior to the surface, it is necessary that the forces acting on the molecule exceed the net force. In other words, work is needed to increase the interfacial surface.
The greater the net intermolecular force, the greater the work to be done and the greater the input of energy. For this reason, interfacial tension is also defined as a function of work or energy, as mentioned below:
Interfacial tension is the work required to create a unit of area at the interface. Likewise, interfacial tension is defined as the free energy needed per unit of area created.
Force Of Tension In Two Dimensions
Consider a hanging pot rack. There are two ropes holding up a 30-kg rack, each at an angle of 15 degrees from the corners of the rack.
To find the tension in either rope, the net force in both the x- and y-directions must be balanced.
Start with the free-body diagram for the pot rack.
Of the three forces on the rack, the force of gravity is known, and it must be balanced equally in the vertical direction by both of the vertical components of the forces of tension.
and because FT1,y= FT2,y :
In other words, each rope exerts a force of 147 N upwards on the hanging pot rack.
To get from here to the total force of tension in each rope, use trigonometry.
The trigonometric relationship of sine relates the y-component, the angle and the unknown diagonal force of tension along the rope on either side. Solving for the tension on the left:
This magnitude would be the same on the right hand side as well, though the direction of that force of tension is different.
What about the horizontal forces each rope exerts?
The trigonometric relationship of tangent relates the unknown x-component to the known y-component and the angle. Solving for the x-component:
Because the horizontal forces are also balanced, this must be the same magnitude of force exerted by the rope on the right, in the opposite direction.
Related Articles
Don’t Miss: Lewis Dot For Ccl4
Pressure Inside A Soap Bubble
To consider the pressure inside the soap bubble, we consider the radius R of the bubble and also the surface tension, gamma, of the liquid .
We begin by assuming no external pressure . You then consider a cross-section through the center of the bubble.
Along this cross section, ignoring the very slight difference in inner and outer radius, we know the circumference will be 2piR. Each inner and outer surface will have a pressure of gamma along the entire length, so the total. The total force from the surface tension is, therefore, 2gamma .
Inside the bubble, however, we have a pressure p which is acting over the entire cross-section pi R2, resulting in a total force of p.
Since the bubble is stable, the sum of these forces must be zero so we get:
2 gamma =porp= 4 gamma / R
Obviously, this was a simplified analysis where the pressure outside the bubble was 0, but this is easily expanded to obtain the difference between the interior pressure p and the exterior pressure pe:
p – pe= 4 gamma / R
Definition Of Tension Formula
Tension is a force working along the length of a medium, especially this force is carried by a flexible medium, like a rope or cable. The flexible cords which carry muscle forces to other parts of the body are known as tendons.
Any flexible connector like a string, rope, chain, wire, or cable, can exert pulls only parallel to its length. Therefore, a force carried by a flexible connector is a tension with a direction parallel to the connector.
It is important to understand that tension is a pull in the connector. The tension force pulls outward along the two ends of the string. This Tension in the rope must equal to the weight of the supported mass, which can be easily proved using Newtons second law. Here, the only external forces acting on the mass will be its weight W and the tension T supplied by the rope. Thus,
Net force = \,
where T and w are the magnitudes of the tension and weight and their signs indicate a direction, with up being positive here. Thus, just as we may expect, the tension equals the weight of the supported mass.
Read Also: What Was The Climate Like In The New England Colonies