What Is Sss In Math

How Do You Respond To Sus

Side Side Side Postulate-> If the three sides of a triangle are congruent to the three sides of another triangle, then the two triangles are congruent. Examples : 1) In triangle ABC, AD is median on BC and AB = AC.

What is SSS reading? The FCAT Reading and Mathematics Sunshine State Standards test was a criterion-referenced test. It assessed student achievement on the knowledge and skills described in the state curriculum framework called the Sunshine State Standards.

Caution Don’t Use Aaa

AAA means we are given all three angles of a triangle, but no sides.

This is not enough information to decide if two triangles are congruent!

Because the triangles can have the same angles but be different sizes:

Without knowing at least one side, we can’t be sure if two triangles are congruent.

Congruent Triangles On A Sphere

As with plane triangles, on a sphere two triangles sharing the same sequence of angle-side-angle are necessarily congruent . This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point thus ASA is valid.

The congruence theorems side-angle-side and side-side-side also hold on a sphere in addition, if two spherical triangles have an identical angle-angle-angle sequence, they are congruent .

The plane-triangle congruence theorem angle-angle-side does not hold for spherical triangles. As in plane geometry, side-side-angle does not imply congruence.

Read Also: What Is The Study Of Geography

Using Two Column Proofs To Prove Triangles Congruent

Triangle Congruence by SSSHow to Prove Triangles Congruent using the Side Side Side Postulate? If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

Triangle Congruence by SASHow to Prove Triangles Congruent using the SAS Postulate? If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

Prove Triangle Congruence with ASA PostulateHow to Prove Triangles Congruent using the Angle Side Angle Postulate? If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.

Prove Triangle Congruence by AAS PostulateHow to Prove Triangles Congruent using the Angle Angle Side Postulate? If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the two triangles are congruent.

Three Ways To Prove Triangles Congruent

A video lesson on SAS, ASA and SSS.

Read Also: Infinite Algebra 1 Multi Step Inequalities

What Is Triangle Congruence

Triangle congruences are the rules or the methods used to prove if two triangles are congruent. Two triangles are said to be congruent if and only if we can make one of them superpose on the other to cover it exactly.

These four criteria used to test triangle congruence include:

Side Side Side , Side Angle Side , Angle Side Angle , and Angle Angle Side .

There are more ways to prove the congruency of triangles, but in this lesson, we will restrict ourselves to these postulates only.

Before going into the detail of these postulates of congruency, it is important to know how to mark different sides and angles with a certain sign which shows their congruency. You will often see the sides and angles of a triangle are marked with little tic marks to specify the sets of congruent angles or congruent sides.

You will see in the diagrams below that the sides with one tic mark are of the same measurement, the sides with two tic marks also have the same length, and the sides with the tic marks are equal. The same goes for the angles.

Triangle Congruence Postulates Sss & Sas Explained W/ 13 Examples

// Last Updated:

Did you know that there are five ways you can prove triangle congruency?

Jenn, Founder Calcworkshop®, 15+ Years Experience

Its true!

In todays geometry lesson, were going to tackle two of them, the Side-Side-Side and Side-Angle-Side postulates.

Youll quickly learn how to prove triangles are congruent using these methods.

In addition, youll see how to write the associated two column proof.

Lets jump in!

So we already know, two triangles are congruent if they have the same size and shape. This means that the pair of triangles have the same three sides and the same three angles .

Thankfully we dont need to prove all six corresponding parts are congruent we just need three!

Why?

Because if we can show specific sides and/or angles to be congruent between a pair of triangles, then the remaining sides and angles are also equal.

But there is a warning we must be careful about identifying the accurate side and angle relationships!

As Math is Fun accurately states, there only five different congruence postulates that will work for proving triangles congruent. So we need to learn how to identify congruent corresponding parts correctly and how to use them to prove two triangles congruent.

Read Also: What Is Psychology Foundations Applications And Integration

Sss Similarity Theorem Examples

Let us take a look at SSS similarity theorem examples.

Check if the given triangles are similar or not.

SSS similarity theorem example, Mouli Javia – StudySmarter Originals

Solution:

Here to determine similar triangles we need to check the proportional sides. So first we will find the ratios of the corresponding sides.

So all the corresponding sides of both the triangles are equal.

Proof Of Sss Congruence Rule

SSS or Side-Side-Side congruence rule states that if three sides of one triangle are equal to three corresponding sides of another triangle, then the triangles are congruent. Let’s perform an activity to show SSS proof. Draw two right-angled triangles with the hypotenuse of 6 inches and one side of 4 inches each. Cut these triangles and try to place one triangle over the other such that equal sides are placed over one another. Do you observe that these two triangles superimpose on each other completely? This means these two triangles are congruent. This completes the SSS proof.

Don’t Miss: What Is Reverse Psychology In Relationships

Congruent Triangles Explanation & Examples

You must be well aware of the photocopy machine. When you put an A4 page inside the machine and activate it, you get an identical copy of that page. If you rotate or flip the page, it will remain the same as the original page. Even if you cut them out, you can line them up again easily. We can say the pages are similar or congruent.

Further, the A4 page is in a rectangular shape, so when you cut it diagonally, you will get the triangle. If you cut both the photocopies in the same manner, you will see both of them form the same kind of a triangle, which has the same sets of angles and sides.

Why Did We Determine The Largest Angle In The First Step

If we know the cosine of an angle, we can easily determine whether the angle is acute or obtuse depending upon the following conditions:

The condition for the acute Angle

$\cos \theta > 0%%EDITORCONTENT%%nbsp for $0^ < \theta < 90^$

The condition for the obtuse Angle

$\cos \theta < 0%%EDITORCONTENT%%nbsp for $90^ < \theta < 180^$

Since the $\gamma 92^$ was obtuse, we already figured out that the angles $\alpha$ and $\beta$ must be acute. This is the reason a single triangle cannot have multiple obtuse angles.

It is also very important to remember that if the largest angle is acute, then the remaining two angles would also be acute.

Example 2

In triangle $ABC$, $a = 24$, $b = 18$ and $c = 29$ cm. Solve the triangle.

Solution:

We are given three sides $a = 24$, $b = 18$, and $c = 29$. Thus, we will apply the three-step method to solve a SSS triangle.

Step 1 of 3

The angle $\gamma$ is opposite the longest side $c = 29$. Thus, we need to find the $\gamma$.

Applying the law of cosines

$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos\:\gamma$

$\cos\:\gamma=\frac$

substituting $a = 24$, $b = 18$ and $c = 29$ in the formula

$\cos\:\gamma=\frac$

$\cos\:\gamma=\frac$

$\cos\:\gamma=\frac$

$\gamma = \cos^ $

$\gamma 86^$

Step 2 of 3

Now it is very straightforward to determine angle. Thus, we will determine the angle $\beta$.

Applying the law of sines

$\frac=\:\frac$

$\sin\:\beta=b\:\frac$

substituting $b = 18$, $c = 29$ and $\gamma = 86.084^$

$\sin\:\beta=18\:\frac}$

$\sin\:\beta=18\:\frac$

You May Like: What Is Curie Temperature In Physics

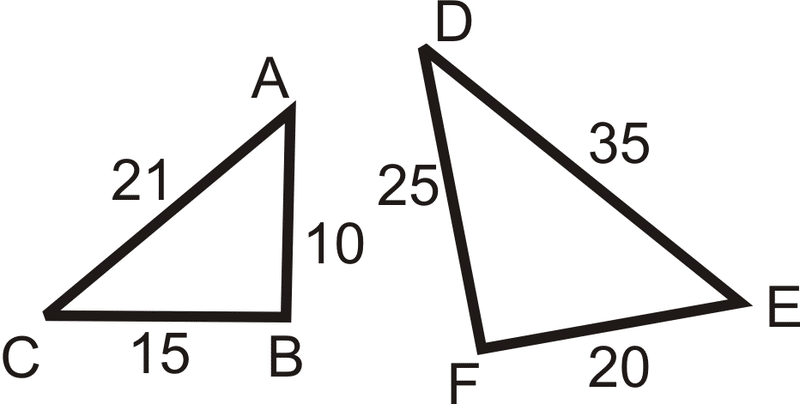
Side Side Side Congruence

Conditions for the SSS – Side Side Side congruence

Two triangles are said to be congruent if three sides of one triangle arerespectively equal to the three sides of the other triangle.

Experiment to prove Congruence with SSS:

Draw LMN with LM = 3 cm, LN = 4 cm, MN = 5cm.

Also, draw another XYZ with XY = 3cm, XZ =4cm, YZ= 5cm.

We see that LM = XY, LN = XZ and MN = YZ.

Make a trace copy of XYZ and try to make it cover LMN with X on L, Y on M and Z on N.

We observe that: two triangles cover each other exactly.

Therefore LMN XYZ

Worked-out problems on side side side congruence triangles :

1. LM = NO and LO = MN. Show that LON NML.

Solution:

LN = NL common

Therefore, LON NML, by side-side-side congruence condition

2. In the given figure, apply SSS congruence condition and state the resultin the symbolic form.

Solution:

LN = NL = 4.5 cm

Therefore, LMN LON, by side side side congruence condition

3. In the adjoining figure, apply S-S-S congruence condition and state the result in the symbolic form.

Solution:

LM = PO = 8.5cm

Therefore, LNM OQP, by Side Side Side congruence condition

4. OLM and NML have common base LM, LO = MN and OM = NL. Which of thefollowing are true?

LMN LMO

LO = MN and OM = NL given

LM = LM common

Thus, MLN LMO, by SSS congruence condition

Therefore, statement is true. So, and statements are false.

5. By Side Side Side congruence prove that ‘Diagonal of the rhombus bisects each other at rightangles’.

Side LO is common

Determining Congruence Of Polygons

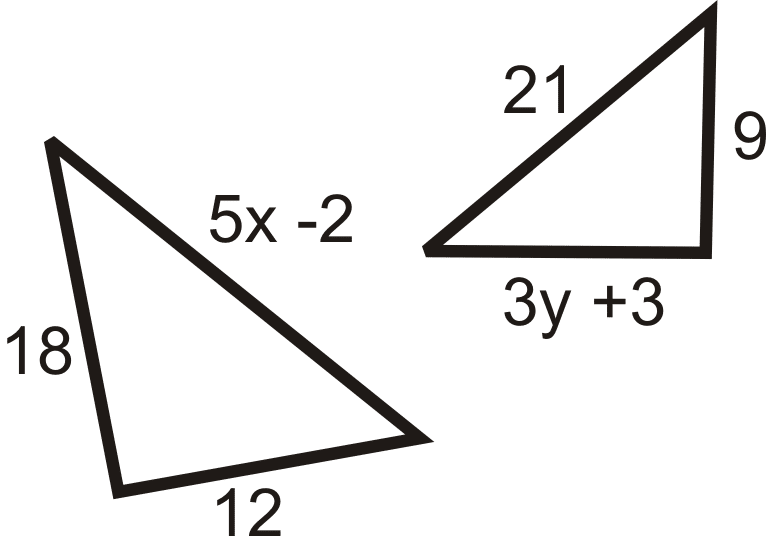
For two polygons to be congruent, they must have an equal number of sides . Two polygons with n sides are congruent if and only if they each have numerically identical sequences side-angle-side-angle-… for n sides and n angles.

Congruence of polygons can be established graphically as follows:

• First, match and label the corresponding vertices of the two figures.
• Second, draw a vector from one of the vertices of the one of the figures to the corresponding vertex of the other figure. Translate the first figure by this vector so that these two vertices match.
• Third, rotate the translated figure about the matched vertex until one pair of corresponding sides matches.
• Fourth, reflect the rotated figure about this matched side until the figures match.

If at any time the step cannot be completed, the polygons are not congruent.

Read Also: Algebra 2 Simplifying Radicals Imaginary Numbers Worksheet

Side Side Side Postulate

A postulate is a statement taken to be true without proof. The SSS Postulate tells us,

Congruence of sides is shown with little hatch marks, like this: . For two triangles, sides may be marked with one, two, and three hatch marks.

If ACE has sides identical in measure to the three sides of HUM, then the two triangles are congruent by SSS:

Definition Of Congruence In Analytic Geometry

In a Euclidean system, congruence is fundamental it is the counterpart of equality for numbers. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.

A more formal definition states that two subsetsA and B of Euclidean spaceRn are called congruent if there exists an isometryf : Rn â Rn ) with f = B. Congruence is an equivalence relation.

Read Also: What Is Osmotic Pressure In Chemistry

Congruence Of Triangles: Conditions

Content Curator| Updated On -Jun 9, 2022

Congruence of triangles is a property of two triangles. Any two triangles are said to be congruent if all the 3 corresponding sides and angles of triangles are equal in measure. Read this entire article to know about the congruence of triangles, conditions for congruence of two triangles, corresponding parts of congruent triangles and solved examples related to congruence of triangles. Two shapes are said to be congruent if their size and shape are the same. Images of two shapes are in a way that the mirror image of one should coincide with the other.

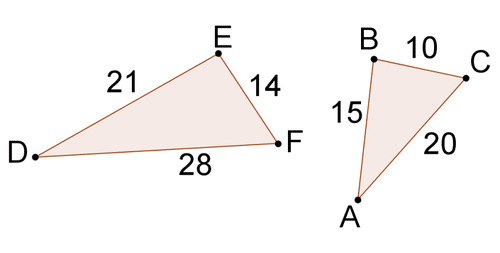
Two triangles are said to be congruent if their all-corresponding sides and angles are equal.

Sides: AB=BC=AC=PQ=QR=PR

Angles: A=B=C=P=Q=R

So, we can say both triangles ABC and PQR are congruent.

Conditions For Congruence Of Triangles

If there are two triangles A and B then if they fulfil any of the below mentioned conditions then they are said to be congruent and they are mentioned like below:

A\ B

A = 40°

Ques2: What is CPCT?

Ans. CPCT stands for Corresponding Parts of Congruent Triangles. It is a theorem which states that if two or more triangles which are congruent to each other then the corresponding angles and sides are also congruent to each other.

Ques3: Is it possible two equilateral triangles are always congruent?

Ans. No it is not always possible. Equilateral triangle angles are of 60 degrees each but it is noy necessary that their sides are always equal.

Ques4: The length of two sides of an isosceles triangle are 5cm and 8 cm, find perimeter of triangle.

Ans. If we consider two sides of isosceles triangles are 5 cm and third one 8 cm then perimeter will be 5 cm+5 cm+8 cm= 18 cm

Ans. In LMN and ONM

LM=ON

MN=NM

Ans.

Read Also: What Is An Experimental Study In Psychology

Congruent Meaning In Maths

The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.

Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is the same as the other.

What Is The Sss Formula

Using the SSS Formula, the congruency or similarity of any two triangles can be checked when two sides and the angle between these sides for both the triangles follow the required criterion. There are different SSS Triangle formulas used to prove the congruence or similarity between two triangles.

SSS Congruence Rule

The Side-Angle-Side theorem of congruency states that, if two sides and the angle formed by these two sides are equal to two sides and the included angle of another triangle, then these triangles are said to be congruent.

The SSS Similarity Rule

The SSS similarity criterion states that if the three sides of one triangle are respectively proportional to the three sides of another, then the two triangles are similar.

Let us see the applications of the SSS formula in the following solved examples section.

Break down tough concepts through simple visuals.

You May Like: What Does The Term Geography Mean

Rules For Triangle Congruency

Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.

We can tell whether two triangles are congruent without testing all the sides and all the angles of the two triangles. In this lesson, we will consider the four rules to prove triangle congruence. They are called the SSS rule, SAS rule, ASA rule and AAS rule.In another lesson, we will consider a proof used for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.

The following diagrams show the Rules for Triangle Congruency: SSS, SAS, ASA, AAS and RHS. Take note that SSA is not sufficient for Triangle Congruency. Scroll down the page for more examples, solutions and proofs.

Triangle Congruency Lesson & Examples

38 min

• Introduction to triangle congruency lesson
• 00:00:13 What are SAS and SSS Postulates?

• Are the triangles congruent by SSS?
• 00:18:12 Write SAS, SSS or Not Congruent
• 00:32:20 Complete the two-column proof
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

You May Like: Algebra 2 Cp Geometric Series Worksheet Answers