Segment Addition Postulate In Geometry

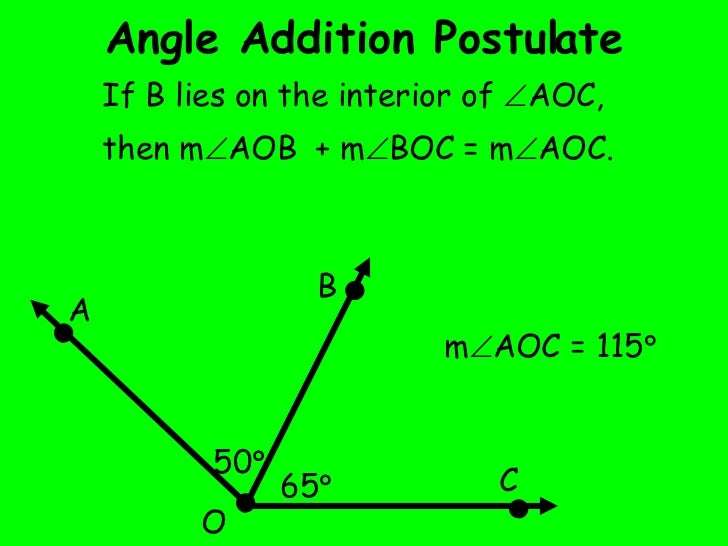
Angle Addition Postulate Definition

The definition of angle addition postulate states that “If a ray is drawn from point O to point P which lies in the interior region of MON, then MOP + NOP = MON”. This postulate can be applied to any pair of adjacent angles in math. In other words, the angle addition postulate can be defined as ‘the sum of two angles joined together through a common arm and a common vertex is equal to the sum of the resulting angle formed’.

Segment Addition Postulate Formula

Based on the definition of the postulate, it is effortless to formulate a definition that follows the theoretical background. This is the basic addition operation, and in this case, it looks like this:

AB + BC = AC

The designations refer to the distance values, respectively, between points A and B, B and C, and A and C.

What Is Angle Addition Postulate In Geometry

The angle addition postulate in geometry is a mathematical axiom which states that if there is a ray drawn from O to Q which is any point inside the region of angle POR, then the sum of angles POQ and QOR is equal to POR. It can be represented in the form of a mathematical equation as POQ + QOR = POR.

Recommended Reading: What Is Isomerism In Chemistry

Use A Manipulative To Teach The Measuring Segments

My advice would be to use blocks or cut outs like these to teach this lesson. I think establishing the connection between these real-world things and the algebra behind the geometry make these postulates much easier to learn. If you just go in with and number line and some numbers on the chalk board it probably wont stick. I even think the measuring segments worksheets you use need to have more realistic pictures and problems in them.

Give them the squares that they can touch and manipulate. They do not have to be anything fancy. You can actually just give them square pieces of precut paper to play around with. Give them a ruler or yard stick, things they can touch and see themselves actually doing in the real world.

Segment Addition Postulate Calculator

• FAQ

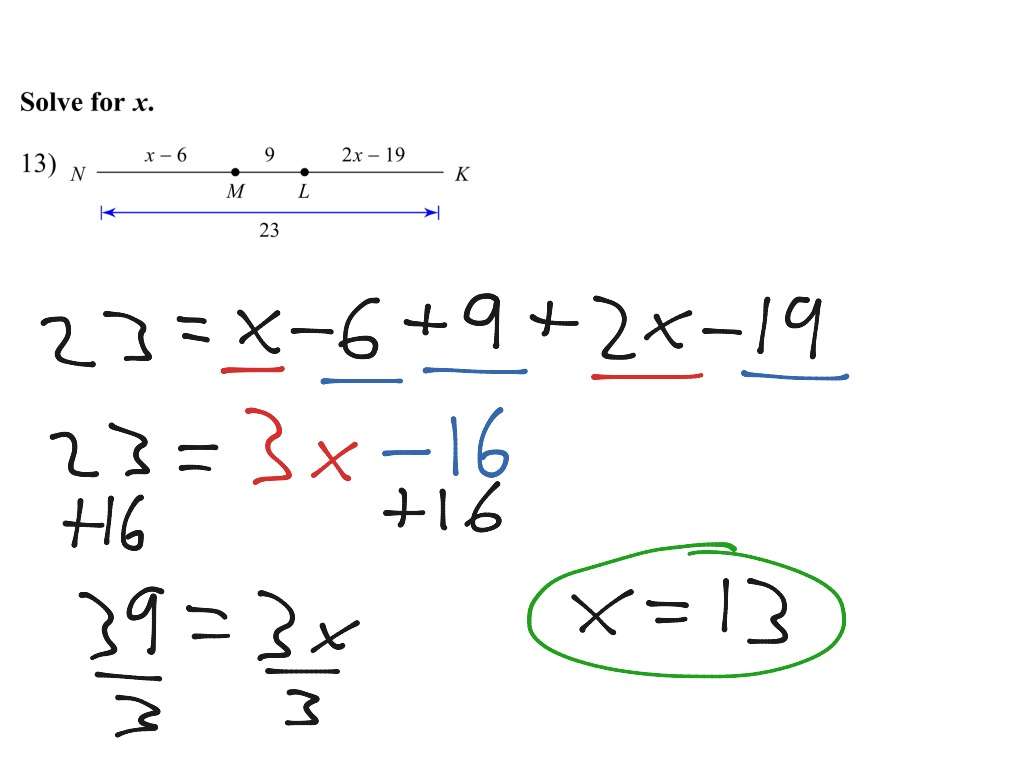
The segment addition postulate calculator allows you to apply this property by addingthe lengths of two adjacent segments and finding the value of the total segment. We will also see the definition of the segment addition postulate, how the segment addition calculator works, and examples of the segment addition postulate.

Recommended Reading: What Is Psychological Well Being

What Does That Actually Mean

So, if you place two angles side by side, they are adjacent. Then the new angle made by both together is the sum of the two original angles.

You can picture this using two arrowheads.

The blue arrowhead has sides BL and UL, so the vertex is L. The tip of the arrow forms the angle BLU which measures 40°.

The green arrowhead has sides GR and NR, so the vertex is R. These three points create GRN which measures 60°.

This has created a new angle measured from side B to N. This is angle BRN.

So in this case

So, there you have it! The BRN is 100°.

Heres a fun tool to play around with and explore how changing the size of two adjacent angles affects the size of their resulting angle.

You will find that changing points A, D, or C will affect the resulting angle it makes, without affecting the adjacent angle.

However notice how the resulting angle changes? This is because it is the sum of the two adjacent angles.

Now you know how the postulate works, lets work through an example and calculate the resulting angle.

As you can see these angles share the same side KL, so they are adjacent.

The angle JKL is a right angle so it is 90°, and from the diagram, you will see LKM is 30°.

You can find their resulting angle as the sum of 90° and 30° so JKM is 120°.

Segment Vs Angle Addition Postulate

For the sake of comparison, we will take the angle addition postulate as an example. The definition of this one tells you that when you place two or more angles next to each other in such a way that their vertices are common, the sum of these adjacent angles is equal to the total sum of the angles.

For instance, the sum of the resulting angle. To apply this, you need to place the corner points next to each other. The main difference between these postulates is that the first one considers the lines. On the other hand, the second deals with the relationship of angles.

Also Check: What Can You Do Masters In Psychology

How Do We Use The Segment Addition Postulate Practically

The practical applications of this segment addition postulate calculator can also be extended to random scenarios as follows:

• You happen to cut a thread into two or more pieces and want to find the total length of the original thread just add up the individual lengths!

• You have bent a stretch of wire to form a rectangle and want to find the total length of the wire just add up the lengths of the individual sides!

• You want to split an ultra-long sandwich among your friends for lunch simply dividethe total length of the sandwich , and enjoy your share!

Some other interesting applications of addition in different contexts are:

The Angle Addition Postulate Angle Pair Relationships Understanding Geometric Diagrams And Notation

Geometry segment addition postulate worksheet answer key. 2 If AC 14 find the value of x. The actual angle is provided on the answer key so in addition to identifying whether an angle is obtuse or acute you can suggest that students mesaure the angle with a protractor and supply. F 32J0 l1 s1X OKeu xtHa2 3SWorfht Hwdadr We9 ULZL 5Ci.

We have a great collection of 100 free geometry worksheets with answer keys for use by teachers students and homeschool parentsmost worksheets contain an answer key and are formatted for fast and easy printing The Angle Addition Postulate Date_____ Period____ 1 Find mKLM Statement Of Purpose For Fine Arts if mKLB 26 and mBLM 60. Angle addition postulate the angle addition postulate states that if. Worksheet angle and segment addition postulate date.

Segment addition postulate worksheet answer key a vector could be used to spell a translation. 0 z um3abd4er vw pi 0t nhm fiynbfgi lnwi0t ye and vgueso gmhe utzr2y p 4 worksheet from kuta software llc kuta software infinite geometry name of the postulated segment given. 20 Write a segment addition problem using three points like question 11 that asks the student to solve for x but has a solution x.

1 If AC 24 find the value of x. December 25 2020 on Geometry Segment Addition Postulate Worksheet Answer Key Kuta Software. 3 if rs 2x 1 and st 3x 2 and rt 24 find the value of x.

S is between d and t. It helps them see the work ahead. Worksheet on acids and bases 20 telugu full movie online.

• Get link

You May Like: What Is Thermite Process In Chemistry

Segment Addition Postulate Calculator Example

In this case, our Segment Addition Postulate Calculator will help you with all the necessary measurements. It calculates the length of the segment line using a formula you probably already know. We will take as an example that you know the value of the distance of points A and B. The distance is 20 cm. Considering that point B is a bisector of the segment line, conclude that the distance of points B and C is also equal to 20 cm.

In the end, the distance of points A and C is equal to the sum of the previous lengths. By entering all of the above, you can get the same values as we stated. It is up to you to try and see for yourself.

How Do We Use The Segment Addition Postulate

Given a line segment AC and a point B in between, if we know the lengths AB and BC, we can find AC using the equation AC = AB + BC.

The segment addition property is used in this segment addition postulate calculator, which also helps you find if a particular point lies on a line segment if the lengths are known.

If the sum of the segments equals the total length, the points must be on the same line, and we say they are collinear. The calculator can check if this is the case by selecting the mode I want to… check if points are collinear.

Recommended Reading: Why Do We Sleep Psychology

Proof In Algebra Geometry Meets Algebra

In a previous blog post about proofs in algebra, I wrote about how to a geometric style proof to solving an algebraic equation. The video embedded into this post models how to justify the solving of an equation with a two-column proof and the justifying of two problems involving the segment addition postulate and the angle addition postulate. Introducing proofs with algebra makes sense. You build upon your knowledge of solving equations to learn the new skill of creating proofs.

To be able to write proofs effectively, you must know definitions, postulate, properties and theorems. As always, I hope this information in the video and blog is helpful. Feel free to comment or ask a question.

What Are The 7 Postulates

Terms in this set

• Through any two points there is exactly one line.
• Through any 3 non-collinear points there is exactly one plane.
• A line contains at least 2 points.
• A plane contains at least 3 non-collinear points.
• If 2 points lie on a plane then the entire line containing those points lies on that plane.

Don’t Miss: How Is Psychology Related To Geography

What Is Segment Addition Postulate In Geometry

The segment addition postulate in geometry is the axiom which states that a line segment divided into smaller pieces is the sum of the lengths of all those smaller segments. So, if we have three collinear points A, B, and C on segment AC, it means AB + BC = AC. It is a mathematical fact that can be accepted without proof.

Segment Bisector Definition And Types

In fact, the human eye can quickly and accurately visually divide things into two equal, symmetrical parts. When we talk about the bisector of a line segment, it denotes the intersection of the segment into two halves or pieces. A bisector can be in the form of apoint, direction, ray, or segment line that will intersect another segment line.

The fundamental characteristic of the bisector is that it always passes through the central part of the segment, dividing it into two parts. It can be vertical, and if it is a bisector in the form of a ray or a direction, it will have infinity.

Don’t Miss: What Is The Geography Of Connecticut

Segment Addition Postulate Examples

Using The Segment Addition Postulate To Solve A Problem

Suppose AC = 48, find the value of x. Then, find the length of AB and the length of BC.AB + BC = AC + = 48

2x + 3x – 4 + 2 = 48

5x – 4 + 2 = 48Add 4 to both sides of the equation.5x – 4 + 4 + 2 = 48 + 45x + 2 = 52Subtract 2 from both sides.5x + 2 – 2 = 52 – 25x = 50Divide both sides by 55x / 5 = 50 / 5x = 10

Now that we have the value of x, we can find the length of AB and the length of BC.

AB = 2x – 4

The length of BC is 32.

Recommended Reading: Do You Capitalize Bachelor’s Degree In Psychology

The Pythagorean Theorem And The Segment Addition Postulate

We also included a segment addition postulate worksheet below. These will include the problems involving distance formula, the Pythagorean Theorem, and the ruler postulate.

We also are giving you a Measuring Segments Worksheet, Exit Quiz, Bell Work Assignment, a Power Point Presentation, and some Segment Addition Postulate Guided Notes!

How To Solve For X With Segment Addition Postulate

If we have a missing length, let’s say x, and we know the total length and the length of the other part of the segment, then we can apply the segment addition postulate to find x. For example, if AB = 3, BC = x, and AC = 5, then we can find x by subtracting AB from AC. This implies AC – AB = 5 – 3 = 2.

You May Like: What Is The Biological Species Concept

Segment Addition Postulate Example

For instance, in a line segment AC, if you know that AB = 10 cm and BC = 20 cm, here’s how you can find the total length of AC:

The extra-cool feature is that if you know the total length and the length of one segment, the calculator will automatically find the length of the other segment for you!

Segment Addition Postulate And The Midpoint

Suppose XA = 3x and AY = 4x – 6. If A is the midpoint of XY, what is the length of XY?

3x 4x – 6_________________________________X A Y

The trick in this problem is to see that if A is the midpoint, then XA = AY.Since XA = AY, 3x = 4x – 6

Subtract 3x from both sides.3x – 3x = 4x – 3x – 60 = x – 6Add 6 to both sides of the equation.0 + 6 = x – 6 + 66 = x

To compute XA, you can either use 3x or 4x – 6Using 3x, we get XA = AY = 3 × 6 = 16

Using 4x – 6, we get XA = AY = 3 × 6 – 6 = 18 – 6 = 12

XY = XA + AY = 16 + 16 = 32

The length of XY is 32.

Read Also: How Did Geography Discourage Greek Unity

Here Are Ten Important Geometry Postulates That You Absolutely Need To Know

Postulate 1.1

Through two points, there is exactly 1 line. Line t is the only line passing through E and F.

Postulate 1.2

Two lines can meet or intersect in exactly 1 point. In the figure below, the point of intersection is called A.

Postulate 1.3

Two planes can intersect in exactly 1 line. The figure below has 2 planes. Plane ZXY in yellow and plane PXY in blue intersect in line XY shown in red.

Postulate 1.4

Through any three points that are not on the same line, there is exactly one plane. Notice that we don’t need 4 points to define a plane. This makes sense since a chair with only 3 legs will not fall over.

The 3 black points determine exactly 1 plane. The 3 red points determine exactly 1 plane.

Postulate 1.5 or ruler postulate

Each point on a line can be assigned a real number. The distance between any 2 points is the absolute value of the difference of the corresponding numbers.

Postulate 1.6 or segment addition postulate

If A, B, and C are collinear, and B is between A and C, AB + BC = AC

For a more thorough coverage of the ruler postulate, check the link above.

Postulate 1.7 or protractor postulate

Let O be the midpoint of line AB. Rays OA, OB, and all the rays with endpoints O that can be drawn on one side of line AB can be paired with the real numbers from 0 to 180 such that OA is paired with 0 degree and OB is paired with 180 degrees.

Postulate 1.8 or angle addition postulate

If AOB is a straight angle, then m AOC + m COB = 180

Postulate 1.9

Postulate 1.10

What Is Segment Addition Postulate In Proofs

The segment addition postulate does not require any proof. It is accepted as a mathematical fact. But many times, we use this axiom in stating proofs for line segments. One such proof is given as “If two congruent segments are added to the line segments of the same length, then their sum is also equal.”

Read Also: What Is Method Of Loci In Psychology