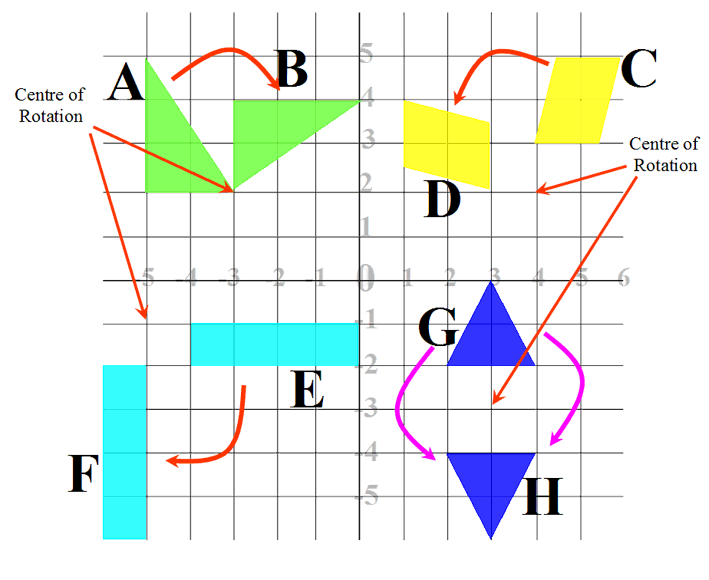
How To Rotate Shapes In Geometry

How To Rotate A Shape Without Using Tracing Paper

To rotate a shape without tracing paper, draw horizontal and vertical arrows from the centre of rotation to each corner of the shape. The new corner can be found by rotating each of these arrows according to the following rules:

For example, rotate the shape 90° clockwise without using tracing paper.

The first step is to draw horizontal and vertical arrows connecting the centre of rotation to a corner on the shape.

The corner selected below is one square right and one square up from the centre of rotation.

Using the rules above, a right-facing arrow will be facing down following a 90° clockwise rotation. An upwards-facing arrow will be facing right after a 90° clockwise rotation.

Instead of the corner being one right and one up, it will now be one down and one right.

Using the new position of this corner, the rest of the shape can be drawn in. The same process can be repeated for all corners to check the result.

Here is another example. Rotate the shape 270° clockwise without using tracing paper.

Draw horizontal and vertical arrows from the centre of rotation to each corner.

After a 270° clockwise rotation all upwards-facing arrows will be facing left and all left-facing arrows will be facing down.

Once all corners are drawn in their new positions, the rotated shape can be drawn by connecting these together.

Now try our lesson on Rotational Symmetry where we learn how to find the order of rotational symmetry for a shape.

Rotate Points On The Coordinate Plane

We will now look at how points and shapes are rotated on thecoordinate plane. It will be helpful to note the patterns of thecoordinates when the points are rotated about the origin atdifferent angles.

A rotation is an isometric transformation: the original figure andthe image are congruent. The orientation of the image also staysthe same, unlike reflections. To perform a geometry rotation, wefirst need to know the point of rotation, the angle of rotation,and a direction . A rotationis also the same as a composition of reflections over intersectinglines.

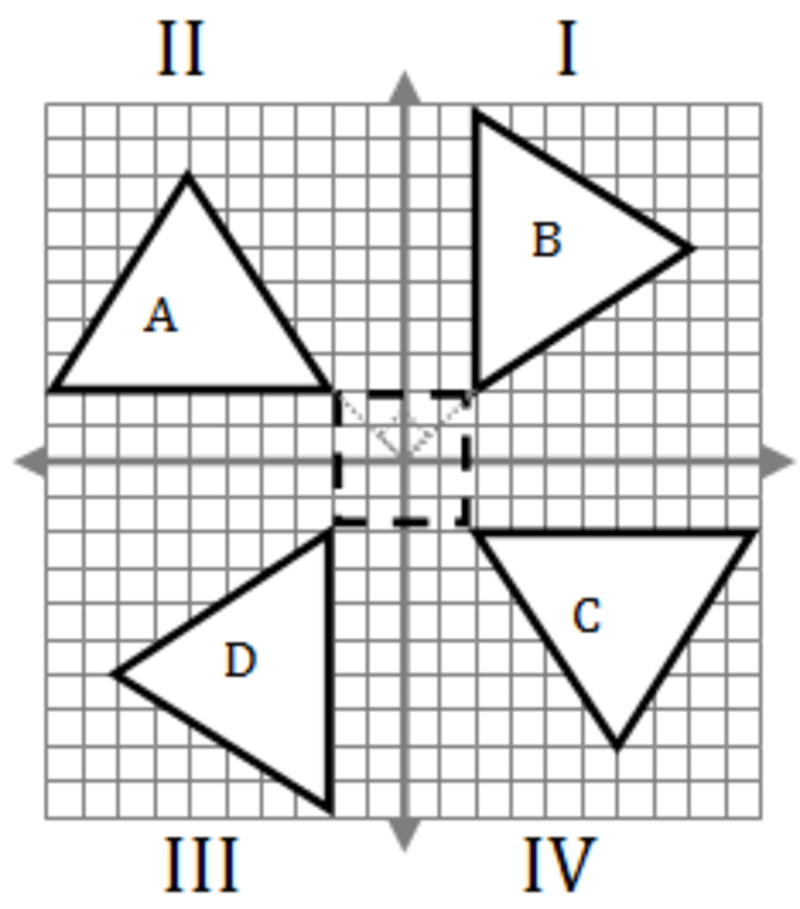
The following diagrams show rotation of 90°, 180° and 270° about the origin. Scroll down thepage for more examples and solutions.

How to rotate points on the coordinate plane?

The following videos show clockwise and anticlockwise rotation of 0, 90, 180and 270about the origin . The pattern of the coordinates are also explored.

Example 0: 90 Degrees Clockwise About The Origin

Since the rotation is 90 degrees, you will rotating the point in a clockwise direction.

Now imagine rotating the entire 4th quadrant one-quarter turn in a clockwise direction:

Point D

Plot Point D

Note the location of Point D, the image of Point D after a -90-degree rotation.

And this process could be repeated if you wanted to rotation Point D -180 degrees or -270 degrees counterclockwise:

Point D after -180 rotation

Point D after -270 rotation

This example should help you to visually understand the concept of clockwise geometry rotations. Next, you will learn the rules for performing clockwise rotations.

> > > Before you move on, take some time to visualize what rotations look like on the coordinate plane.

< > < > < >

Don’t Miss: Who Is The Father Of Modern Physics

The Angle Of Rotation

Given an object, its image and the center of rotation, we can find the angle of rotation using thefollowing steps.

Step 1: Choose any point in the given figure and join thechosen point to the center of rotation.

Step 2: Find the image of the chosen point and join it tothe center of rotation.

Step 3: Measure the angle between the two lines. The signof the angle depends on the direction of rotation. Anti-clockwise rotation is positive and clockwiserotation is negative.

Example:Figure ABC is the image of figure ABC. O is the center of rotation.Find the angle of rotation.

Solution:Step 1: Join A to O.

Step 2: Join A to O.

Step 3: Measure the angle AOA.

The angle of rotation is 62 anticlockwise or +62

Manual rotation of a polygon about a given point at a given angle

You will need a straightedge, a protractor, and a compass. We will perform rotations about apoint inside the figure, one outside the figure and one on the figure.

Examples:

• Show Video Lesson

Linear And Multilinear Algebra Formalism

When one considers motions of the Euclidean space that preserve the origin, the distinction between points and vectors, important in pure mathematics, can be erased because there is a canonical one-to-one correspondence between points and position vectors. The same is true for geometries other than Euclidean, but whose space is an affine space with a supplementary structure see an example below. Alternatively, the vector description of rotations can be understood as a parametrization of geometric rotations up to their composition with translations. In other words, one vector rotation presents many equivalent rotations about all points in the space.

A motion that preserves the origin is the same as a linear operator on vectors that preserves the same geometric structure but expressed in terms of vectors. For Euclidean vectors, this expression is their magnitude . In components, such operator is expressed with n×northogonal matrix that is multiplied to column vectors.

As it was already stated, a rotation is different from an arbitrary fixed-point motion in its preservation of the orientation of the vector space. Thus, the determinant of a rotation orthogonal matrix must be 1. The only other possibility for the determinant of an orthogonal matrix is 1, and this result means the transformation is a hyperplane reflection, a point reflection , or another kind of improper rotation. Matrices of all proper rotations form the special orthogonal group.

x

=e^ /2},}

Read Also: What Does Fg Mean In Physics

What Is A Rotation In Geometry

A rotation in geometry is a transformation that has one fixed point. The geometric object or function then rotates around this given point by a given angle measure. This measure can be given in degrees or radians, and the direction clockwise or counterclockwise is specified.

The most common point of rotation is the origin . The point of rotation may be a vertex of a given object or its center in other situations.

Rotating Shapes And Coordinates

Questions on rotation can be combined with coordinates. For example, a child might be shown this shape:They might be asked the following question:

If this shape is rotated 90 clockwise about point B, what will the co-ordinates of point A be on the newly rotated shape?

They would then need to rotate the shape and see where point A would be on the rotated shape .

Read Also: How To Do Math Problems

What Does It Mean To Rotate A Shape

Rotating a shape means to change its direction by turning it. The size and shape do not change during rotation. A shape is often rotated about a specific point called the centre of rotation. We also need to know what angle and direction the shape is rotated in.

For example, this triangle has been rotated 90° counter-clockwise about the point.

You can tell that a shape has been rotated because it is not facing the same direction as it was originally. The original shape is called the object and the rotated shape is called the image.

When rotated, a shape remains the same distance away from the centre of rotation. It is just in a different direction.

How To Rotate A Point

The demonstration below that shows you how to easily perform the common Rotations . There is a neat ‘trick’ to doing these kinds of transformations. The basics steps are to graph the original point , then physically ‘rotate’ your graph paper, the new location of your point represents the coordinates of the image. It’s much easier to understand these steps if you watch the visual demonstration below.

You May Like: Algebra 1 Solving Systems Of Equations By Substitution Worksheet

Video Lesson & Examples

• Draw the image given the rotation
• 00:16:41 Find the coordinates of the vertices after the given transformation
• 00:19:03 How to describe the rotation after two repeated reflections
• 00:26:32 Identify rotational symmetry, order, and magnitude of the rotation?
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

How To Rotate Shapes

Children need to have a good knowledge of angles before they can carry out tasks involving rotating shapes. They need to know off-by-heart that 90 is a quarter turn, 180 degrees a half turn, 270 a three-quarter turn and 360 a full turn.

They may be given a shape like the following one in blue and asked to rotate it 90 clockwise about the vertex marked with the red dot:They should end up with a new shape like this:Alternatively, they may be given a shape and asked to rotate it about its centre. In this case, someone started with the pink shape and rotated it 180 anticlockwise about the vertex marked with the red cross, resulting in the green shape:It is a good idea to give children cut-out shapes so that they can physically rotate the shapes to gain a better understanding of this concept. They then need to move onto being able to work out how to rotate the shapes without this support.

You May Like: Differential Equations And Linear Algebra 4th Edition

How To Rotate A Shape Using Tracing Paper

To rotate a shape using tracing paper:

The easiest way to rotate a shape is to use tracing paper.

For example, use tracing paper to rotate the shape 90° clockwise about the point.

After a 90° clockwise rotation, the upwards arrow is facing right. Use the grid lines of the paper to help line up the arrow correctly, ensuring that it is completely horizontal.

Then draw in the shape below.

Here is another example. Rotate the shape 270° clockwise about the point using tracing paper.

Every lot of 90° is equivalent to a quarter turn. 270° is 3 lots of 90° and so, 270° is equivalent to three-quarters of a turn.

The upward-facing arrow will be facing to the left after a 270° clockwise rotation.

We draw the shape in below.

Example : Describe A Rotation

Describe the rotation of shape A to shape B

Trace the shape.

Use a pencil and trace the object shape onto a piece of tracing paper.

Rotate the tracing paper.

Have a think about where the centre of rotation might be. Use the pencil and put the tip onto that point. Pivot the tracing paper to check. It may take a few tries until you find the correct centre of rotation.

Write down the description.

Make sure you state that it is a rotation. Then give the angle of rotation and if necessary the direction of rotation. Also give the coordinates of the centre of rotation.

Rotation 180^o about the point

Since the rotation is a half-turn, no direction is needed.

Since the rotation was 180^o, if we connect the vertices in corresponding pairs, these lines all cross at the centre of rotation.

Don’t Miss: Algebra Functions Examples With Answers

Lesson Explainer: Rotations About A Point Mathematics

In this explainer, we will learn how to rotate points, line segments, and shapes about given points.

In geometry, we often use the congruence of shapes, angles, and line segments to prove results. This means that we want to find methods of checking the congruence of these objects. Often, this involves comparing the properties of two of these objects, but this is not the only way of studying congruence.

We can also ask, What transformation can we apply to an object that does not affect its size or shape? If a transformation does not affect these properties, then we can apply the transformation to any object to construct a congruent object. In particular, if we can show that two objects differ by one or more of these transformations, then we can conclude they are congruent.

There are many different transformations that do not affect the size or shape of an object we can slide the object around, changing its position , we can find a mirror image of the object , and we can also rotate the object about a point .

We will focus on rotating objects about a point. To start this, lets consider exactly what rotation is. A rotation is defined by the center of the rotation and the amount of the rotation. In particular, we rotate each point around a circle centered at the center of the rotation. For example, lets say we have the following rotation of a point

Related Definitions And Terminology

The rotation group is a Lie group of rotations about a fixed point. This fixed point is called the center of rotation and is usually identified with the origin. The rotation group is a point stabilizer in a broader group of motions.

For a particular rotation:

• The axis of rotation is a line of its fixed points. They exist only in n> 2.
• The plane of rotation is a plane that is invariant under the rotation. Unlike the axis, its points are not fixed themselves. The axis and the plane of a rotation are orthogonal.

A representation of rotations is a particular formalism, either algebraic or geometric, used to parametrize a rotation map. This meaning is somehow inverse to the meaning in the group theory.

Rotations of spaces of points and of respective vector spaces are not always clearly distinguished. The former are sometimes referred to as affine rotations , whereas the latter are vector rotations. See the article below for details.

Also Check: What Is Psychology Of Women

Ways To Rotate A Shape

These 3 methods to rotate a shape were super helpful for my students!

Rotating a shape can be a difficult concept for both students and teachers. After seeing my students struggle with this topic, I came up with a few strategies to make rotations easier.

These 3 strategies work with different levels of learners. I encourage you to try all 3!

This article contains affiliate links to products. I may receive a commission for purchases made through these links.

Rotations Are Direct Isometries

Rotation notation is usually denoted R

• “Center” is the ‘center of rotation.’ This is the point around which you are performing your mathematical rotation.
• “Degrees” stands for how many degrees you should rotate. A positive number usually by convention means counter clockwise.

A rotation is a direct isometry , which means that both the distance and orientation are preserved.

As you can see in diagram 1 below, triangle $$ \triangle ABC $$ is rotated by $$90^$$ to its image $$ \triangle A’B’C’ $$. And the distance between each of the vertices of the preimage is maintained in its image.

$m \overline = 4 \\m \overline = 4 \\\\m \overline = 5 \\m \overline = 5 \\\\m \overline = 3 \\m \overline = 3 $

You can also see that the orientation of the letters is preserved, i.e. that the vertices in the original shape are ordered $$ABC$$ , in clockwise order, and that the image maintains the same clockwise order, making rotations a direct isometry.

Don’t Miss: How To Do Unit Conversions In Chemistry

Example : Rotate A Shape About A Fixed Point

Rotate the shaded shape 90^o clockwise about the fixed point:

Use a pencil and trace the shape onto a piece of tracing paper.

2Rotate the tracing paper about the centre of enlargement.

Use the pencil and put the tip onto the fixed point. Pivot the tracing paper a quarter turn clockwise.

3Draw the rotated shape onto the grid.

Carefully lift the tracing paper and draw the rotated shape in the correct position.

Note: one of the vertices of the triangle has not moved. This is also known as an invariant point of the shape.

Rules For Rotating A Shape About The Origin

The rules for rotating shapes using coordinates are:

How to Rotate a Shape by 90 Degrees

To rotate shape 90° clockwise about the origin, all original coordinates becomes . To rotate a shape 90° counter-clockwise about the origin, the coordinates become . Simply switch the x and y coordinates and multiply the coordinate with the negative sign by -1.

For example, use the rule to to rotate the shape 90° clockwise.

To use this rule, simply switch the to and then make the 3 negative to get .

How to Rotate a Shape by 180 Degrees

To rotate a shape by 180° clockwise or counter-clockwise, the rule is to replace the coordinates with . For example, a coordinate at will move to after a 180° rotation.

Simply multiply each coordinate by -1 to rotate a shape 180°.

If a coordinate is negative, it will become positive after a 180° rotation. For example, the coordinate , will move to after a 180° rotation.

How to Rotate a Shape by 270 Degrees

To rotate shape 270° clockwise about the origin, all original coordinates becomes . To rotate a shape 270° counter-clockwise about the origin, the coordinates become . Simply switch the x and y coordinates and multiply the coordinate with the negative sign by -1.

For example, to rotate the point 270° clockwise, it becomes . Simply switch the x and y coordinates to get and then multiply the 1 by -1 to get .

You May Like: What Is Archimedes Principle In Physics