Characteristics Of Sound Waves
Following are the characteristics of sound waves.
- The waves crest is its highest point.
- The trough is the lowest point of the wave.
- A wave is formed by one crest and one trough. The distance between one crest/trough and the next is measured in wavelength.
- Wave height is the distance between the trough and the crest.
- The wave steepness is defined as the ratio of wave height to wavelength.
- The amplitude is the distance between the waves center and the bottom of the trough.
- The wave period is the amount of time it takes for one full wavelength to pass through a specific place.
Period Frequency And Amplitude
- The period is the time taken for one oscillation cycle.
- The frequency is defined as the inverse of the period. It refers to how many cycles it completes in a certain amount of time, \.
- The period of an object oscillating in simple harmonic motion is related to theangular frequencyof the object’s motion, \ and \.
- The amplitude is the maximum displacement from the equilibrium position in an oscillation. It is an important property that is related to the energy of a wave. The amplitude is not affected by a wave’s period or frequency. There can be two waves with the same frequency, but with different amplitudes.
- Trigonometric functions are used to model waves and oscillations, so we use these equations to find the amplitude and period, \\). To determine the amplitude, \. To determine the period, \.
Characteristics Of Simple Harmonic Motion
A very common type of periodic motion is called simple harmonic motion . A system that oscillates with SHM is called a simple harmonic oscillator.
Simple Harmonic Motion
In simple harmonic motion, the acceleration of the system, and therefore the net force, is proportional to the displacement and acts in the opposite direction of the displacement.
A good example of SHM is an object with mass m attached to a spring on a frictionless surface, as shown in . The object oscillates around the equilibrium position, and the net force on the object is equal to the force provided by the spring. This force obeys Hookes law _=\textkx, as discussed in a previous chapter.
If the net force can be described by Hookes law and there is no damping , then a simple harmonic oscillator oscillates with equal displacement on either side of the equilibrium position, as shown for an object on a spring in . The maximum displacement from equilibrium is called the amplitude . The units for amplitude and displacement are the same but depend on the type of oscillation. For the object on the spring, the units of amplitude and displacement are meters.
What is so significant about SHM? For one thing, the period T and frequency f of a simple harmonic oscillator are independent of amplitude. The string of a guitar, for example, oscillates with the same frequency whether plucked gently or hard.
Recommended Reading: Glencoe Algebra 2 Chapter 5 Answer Key
Period Frequency And Amplitude Of Trigonometric Functions
Trigonometric functions are used to model waves and oscillations. This is because oscillations are things with periodicity, so they are related to the geometric shape of the circle. Cosine and sine functions are defined based on the circle, so we use these equations to find the amplitude and period of a trigonometric function.
$$y=a\ c\mathrm\left$$
The amplitude will be given by the magnitude of \.
$$\mathrm=\left|a\right|$$
The period will be given by the equation below.
$$\mathrm=\frac$$
The expression for the position as a function of the time of an object in simple harmonic motion is given by the following equation.
$$x=A\cos\left$$
Where \ is the amplitude in meters, \, and \ is time in seconds,\.
From this equation, we can determine the amplitude and period of the wave.
$$\mathrm=\left|A\right|$$
$$\mathrm=\fracT}\right|}=T$$
Relationship Between Period Frequency And Amplitude
The period, frequency, and amplitude are all related in the sense that they are all necessary to accurately describe the oscillatory motion of a system. As we will see in the next section, these quantities appear in the trigonometric equation that describes the position of an oscillating mass. It is important to note that the amplitude is not affected by a wave’s period or frequency.
It is easy to see the relationship between the period, frequency, and amplitude in a Position vs. Time graph. To find the amplitude from a graph, we plot the position of the object in simple harmonic motion as a function of time. We look for the peak values of distance to find the amplitude. To find the frequency, we first need to get the period of the cycle. To do so, we find the time it takes to complete one oscillation cycle. This can be done by looking at the time between two consecutive peaks or troughs. After we find the period, we take its inverse to determine the frequency.
Displacement as a function of time for simple harmonic motion to illustrate the amplitude and period. Distance from \ to \ is the amplitude, while the time from \ to \ is the period, StudySmarter Originals
Read Also: How Did Geography Discourage Greek Unity
What Are Amplitude Frequency And Period
The amplitude is the maximum displacement from the equilibrium position in an oscillation. It is an important property that is related to the energy of a wave. The period is the time taken for one oscillation cycle. The frequency is defined as the inverse of the period. It refers to how many cycles it completes in a certain amount of time.
The Attempt At A Solution
- 0
Maxx573 said:Looking at the conservation of energy:K = \frac kA^2\sin^2 = \fracmv^2U = \frac kA^2\cos^2 = \frackx^2E = \frackA^2 = \fracmv^2 + \frackx^2OK, obviously something here should help me, but I just keep running into the same things. When U = E, then x = A and v = 0. When K = E, then a = 0 and t = 0. Acceleration is at its maximum when all the energy is potential energy , and velocity is at its maximum when the spring is at equilibrium .All of this makes perfect sense to me, but I haven’t been able to apply it to solving for A or x without already knowing one of them. I feel like the answer is staring me in the face, but I just can’t find it.
alphysicist said:In setting up this problem I would say there are three types of energies to keep track of: kinetic, gravitational potential, and spring potential. The two points you are interested in are the initial position, and the lowest point in the motion.What is the kinetic, gravitational potential, and spring potential energies at the intial point? at the final point? Setting the total energy at the initial point equal to the total energy at the final point should give you the answer.
Read Also: What Does Mixture Mean In Chemistry
Is Amplitude Always Positive
Amplitudes are always positive numbers and are never negative . Amplitudes are positive because distance can only be greater than zero or equal to zero negative distance does not exist.
George Jackson is the founder and lead contributor of Physics Network, a popular blog dedicated to exploring the fascinating world of physics. George has always been passionate about physics and its ability to explain the fundamental workings of the universe. He received his Ph.D. in physics from the University of California, Berkeley, where he conducted research on particle physics and cosmology. After completing his degree, George worked as a postdoctoral researcher at CERN, the world’s largest particle physics laboratory. It was there that he first had the idea to create a resource for physics enthusiasts of all levels to learn about and discuss the latest developments in the field. When he’s not busy exploring the mysteries of the universe, George enjoys hiking and spending time with his family.
How To Calculate The Amplitude Of Motion
We have understood what is amplitude of motion now the next question that arises is how to calculate the amplitude of motion. The simple harmonic motion is a sinusoidal wave function therefore, the SHM equation can be represented as a function of sine or cosine.
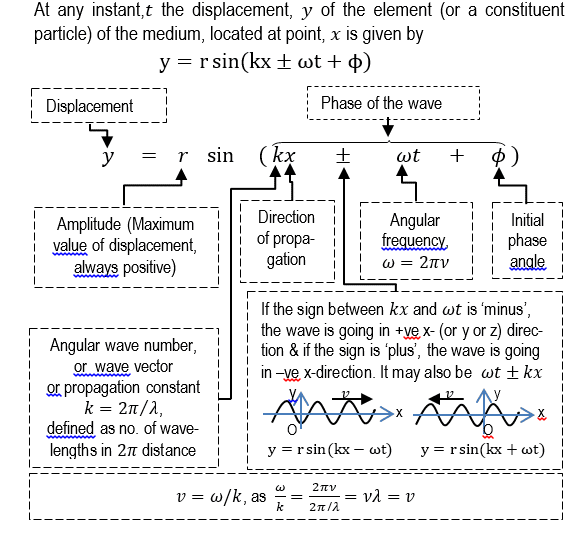
x = A sin or x = A cos
Here,
x is the displacement of the wave
A is the amplitude of motion
is the angular frequency
t is the period
is the phase angle
From the above equation, we can calculate the amplitude of the motion.
Suppose we are given the SHM equation as x = 2sin. Now, comparing the equation with sinusoidal wave equation x = A sin , we get amplitude as 2 metres.
For the given diagram, we can easily calculate the amplitude. From the figure, the amplitude is 5 m.
Don’t Miss: What Is R And S In Chemistry
The Relationship Between Wave Frequency Period Wavelength And Velocity
Since wave frequency is the number of waves per second, and the period is essentially the number of seconds per wave, the relationship between frequency and period is
just as in the case of harmonic motion of an object. We can see from this relationship that a higher frequency means a shorter period. Recall that the unit for frequency is hertz , and that 1 Hz is one cycleâor one waveâper second.
The speed of propagation vw is the distance the wave travels in a given time, which is one wavelength in a time of one period. In equation form, it is written as
From this relationship, we see that in a medium where vw is constant, the higher the frequency, the smaller the wavelength. See Figure 13.8.
Amplitude Period And Frequency
Here is a ball moving back and forth with simple harmonic motion :
Its position \ as a function of time \ is:
\ = A \cdot \cos \Bigl\)
where \ is the amplitude of motion: the distance from the centre of motion to either extreme
\ is the period of motion: the time for one complete cycle of the motion.
Don’t Miss: What Is Oxidizing Agent In Chemistry
University Physics Volume 1
- Define the terms period and frequency
- List the characteristics of simple harmonic motion
- Explain the concept of phase shift
- Write the equations of motion for the system of a mass and spring undergoing simple harmonic motion
- Describe the motion of a mass oscillating on a vertical spring
When you pluck a guitar string, the resulting sound has a steady tone and lasts a long time ). The string vibrates around an equilibrium position, and one oscillation is completed when the string starts from the initial position, travels to one of the extreme positions, then to the other extreme position, and returns to its initial position. We define periodic motion to be any motion that repeats itself at regular time intervals, such as exhibited by the guitar string or by a child swinging on a swing. In this section, we study the basic characteristics of oscillations and their mathematical description.
Figure 15.2 When a guitar string is plucked, the string oscillates up and down in periodic motion. The vibrating string causes the surrounding air molecules to oscillate, producing sound waves.
Definition Of Amplitude And Period

- Posted 6 years ago. Direct link to Rakesh Reddy’s post Shouldn’t the amplitude g…moreShouldn’t the amplitude get lower and lower with each cycle? If you imagine a spring that has been extended and then let go, it wouldn’t come back to the original position after one cycle, rather it would be slightly less displaced. Am I missing something?AnswerAnswer Rakesh Reddy’s post Shouldn’t the amplitude g…Button opens signup modal
You May Like: Why Is Statistics Important In Psychology
What Is Amplitude In Physics
As we hearsound every day and sometimes we enjoy it as well while sometimes we get irritated. Here, we will learn about a few terms which are related to sound. The term amplitude in physics is said to be the maximum displacement or distance that is moved by a point on a body that is vibrating orwave measured from itsequilibrium position. It is more or less said to be equal to one-half the length of the vibration path. The amplitude of a pendulum is thus one-half the distance that the bob traverses in moving from one side to the other while oscillating. Waves are generated by the source which is vibrating.
The definition of amplitude in Physic refers to the length and width of waves, such as sound waves, as they move or vibrate. Moreover, Amplitude is also known as a measure of the intensity, loudness, power, strength, or volume level of a signal. For instance In an electrical circuit operating on alternating current , the amplitude is measured as the Voltage level and is expressed as +V and V, depending on the direction of the current.
Define Amplitude In Physics
The amplitude which is the peak-to-peak amplitude that is the abbreviated pp is the change between peaks that is the highest amplitude value. The lowest amplitude value can be negative as well. So with appropriate circuitry, we can say that the peak-to-peak amplitudes of electric oscillations can be measured by meters or by viewing the waveform on an oscilloscope.
The p-p or the peak-to-peak amplitude is a straightforward measurement on an oscilloscope. That way we can say the peaks of the waveform are easily identified and measured against the graticule. This generally remains as a common way of specifying amplitude but sometimes we can say that the other measures of amplitude are more appropriate.
For alternating currentelectric power generally, the universal practice is to specify RMS values of a sinusoidal waveform.
Don’t Miss: Glencoe Algebra 1 Chapter 6 Answer Key
Amplitude Period And Phase Shift Calculator
The amplitude period phase shift calculator is used for trigonometric functions which helps us in the calculations of vertical shift, amplitude, period, and phase shift of sine and cosine functions with ease. We have to enter the trigonometric equation by selecting the correct sine or the cosine function and clicking on calculate to get the results.
Amplitude Of A Wave Formula
Formula to find amplitude of wave is Position = amplitude * sine function
Amplitude of a wave is found directly from mathematical form of wave that is y=Asin. Amplitude is equal to A.
The above equation is formula to find amplitude of a wave. This formula can be used to find time period T, frequency , displacementy, phase difference and wavelength of a wave.
Recommended Reading: What Does K Stand For In Math
Period Frequency And Amplitude: Definitions
Period, frequency, and amplitude are important properties of waves. As we mentioned before, the amplitude is related to the energy of a wave.
The amplitude is the maximum displacement from the equilibrium position in an oscillation
The period is the time taken for one oscillation cycle. The frequency is defined as the reciprocal of the period. It refers to how many cycles it completes in a certain amount of time.
Theperiodis the time taken for one oscillation cycle.
The frequencydescribes how many oscillation cycles a system completes in a certain amount of time.
For example, a large period implies a small frequency.
$$f=\frac1T$$
Where \is the frequency in hertz, \,and\is the period in seconds, \.
Period Frequency And Amplitude: Examples
To visualize these concepts experimentally, imagine you and your friend grabbing a rope by the ends and shaking it up and down such that you create a wave that travels through the rope. Let’s say that in one second, the rope completed two cycles. The frequency of the wave would be \. The period would be the inverse of the frequency, so the period of the wave would be half a second, meaning it would take half a second to complete one oscillation cycle.
A student observing an oscillating block counts \. Determine its frequency and period.
$$f=45.5\ }\min}\times\frac1}=0.758\ }}$$
$$f=0.758\ \mathrm$$
$$T=\frac1f=\frac1}=1.32\ \mathrm s$$
The period for an object oscillating in simple harmonic motion is related to theangular frequencyof the object’s motion. The expression for the angular frequency will depend on the type of object that is undergoing the simple harmonic motion.
$$\omega=2\pi f$$
$$T=\frac\omega$$
Where \ is the angular frequency in radians per second, \.
The two most common ways to prove this are the pendulum and the mass on a spring experiments.
Theperiod of a spring is given by the equation below.
$$T_s=2\pi\sqrt$$
Where \is the mass of the object at the end of the spring in kilograms, \, and \is the spring constant that measures the stiffness of the spring in newtons per meter, \.
A block of mass \ is attached to a spring whose spring constant is \. Calculate the frequency and period of the oscillations of this springblock system.
$$T_p=2\pi\sqrt$$
Read Also: What Is Sum In Math
Is The Amplitude Half The Height
Wave height the vertical distance between the crest of a wave and its neighboring trough. This term is commonly used when describing water waves where the undisturbed surface is not easily determined. Amplitude the amount of displacement from the equilibrium or rest position. Equal to one half the wave height.
The Period And Frequency Of A Mass On A Spring

One interesting characteristic of the SHM of an object attached to a spring is that the angular frequency, and therefore the period and frequency of the motion, depend on only the mass and the force constant, and not on other factors such as the amplitude of the motion. We can use the equations of motion and Newtons second law to find equations for the angular frequency, frequency, and period.
Consider the block on a spring on a frictionless surface. There are three forces on the mass: the weight, the normal force, and the force due to the spring. The only two forces that act perpendicular to the surface are the weight and the normal force, which have equal magnitudes and opposite directions, and thus sum to zero. The only force that acts parallel to the surface is the force due to the spring, so the net force must be equal to the force of the spring:
Substituting the equations of motion for x and a gives us
Cancelling out like terms and solving for the angular frequency yields
The angular frequency depends only on the force constant and the mass, and not the amplitude. The angular frequency is defined as \omega =2\pi \textT, which yields an equation for the period of the motion:
The period also depends only on the mass and the force constant. The greater the mass, the longer the period. The stiffer the spring, the shorter the period. The frequency is
Don’t Miss: What Is Angle In Math