When Do Children Learn About Vertices Faces And Edges In Primary School
Children need to be formally introduced to the vocabulary of vertices, faces and edges in Year 2 when studying geometry. However, teachers may make the choice to introduce this vocabulary earlier on.
Year 2 pupils should be able to:
- identify and describe the properties of 3-D shapes, including the number of edges, vertices and faces
The non-statutory guidance states that:
- Pupils handle and name a wide variety of common 2-d and 3-d shapes including: quadrilaterals and polygons, and cuboids, prisms and cones, and identify the properties of each shape . Pupils identify, compare and sort shapes on the basis of their properties and use vocabulary precisely, such as sides, edges, vertices and faces.
From this point on, the national curriculum does not reference vertices, faces and edges explicitly again, so teachers in other year groups will have to continue to use this vocabulary when looking at shape
Edge Definition Illustrated Mathematics Dictionary
What Is The Edge Of A Cube
Math Fun Library: Question : How does ‘Deduce’ relate to Deduction ? Answer : Deduction is a noun derived from the verb Deduct. If derived from Deduce it means to infer, to draw conclusions by reasoning from given principles. To sieve out all the unnecessary information from a problem and draw out the plain facts In other words, you can think of frequency in an image as the rate of change. Parts of the image that change rapidly from one color to another contain high frequencies, and parts that change gradually contain only low frequencies
Recommended Reading: Holt Geometry Homework And Practice Workbook Answer Key
What Is Edge In Triangle
Edges are the lines that join to form vertices. A square has four edges and four vertices. A triangle has three of both. A square pyramid, a three-dimensional shape, has different numbers of edges and vertices. It has five vertices, or corners, but it has eight edges to join these vertices together.
What Is A Face In Math Study
edge definition: 1. the outer or furthest point of something: 2. the side of a blade that cuts, or any sharp part. Learn more Basic math in JavaScript numbers and operators. At this point in the course we discuss math in JavaScript how we can use operators and other features to successfully manipulate numbers to do our bidding. Basic computer literacy, a basic understanding of HTML and CSS, an understanding of what JavaScript is Beyond this, it is not only spheres which come in exotic versions. It is now known that 4-dimensional space itself comes in a variety of flavours. There is the usual flat space, but alongside it are the exotic R 4 s. Each of these is topologically identical to ordinary space, but not differentially so Math. Club O 30 2008Oct. 30, 2008 A graphis a bunch of vertices connected by edges. The simplest example for the talk is the tetrahedron K 4. A primein a graph is a closed path in the graph minimizing the number of edges traversed. This means no backtrack, no tails. Go around only once. Orientation counts. Starting point doesndoesnt count’t.
Recommended Reading: Holt Geometry Answers
What Are Vertices In Math
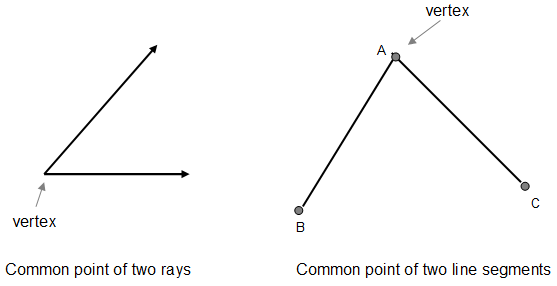
Vertices are the points, or corners, in geometrical and mathematical shapes where two or more lines meet but do not cross, according to Math Open Reference. Vertices can exist in two-dimensional and three-dimensional shapes. The singular form of vertices is vertex. Sometimes, the term vertex is also used to describe certain points on quadratic equations.
Vertices are often used as a description of the corner of a shape, generally a polygon. However, they can also exist at a point between any two lines which meet and form an angle but do not cross. If the lines cross, the point is considered an intersection and not a vertex. Vertices are a useful way to describe objects and their placement in two-dimensional and three-dimensional spaces. Two-dimensional objects have vertices where their lines meet, and three-dimensional objects have vertices where their planes meet. In this sense, vertices can sometimes be described as the corners of a geometric structure.
In mathematics, the term vertex can also refer to the peak of a parabola. A parabola is a curved shape that is generated by graphically representing a quadratic equation. The peak of a parabola is either the highest or lowest point on the curve, depending on whether it opens upwards or downwards.
Definition And Meaning Of Vertices And Edges
A vertex refers to a single point which joins edges together in a shape. Many individuals also call a vertex as a corner or a point. Furthermore, a vertex is where two lines meet. Every corner which exists in a geometrical shape represents a vertex.
The angle is certainly irrelevant to whether or not a corner is a vertex. Furthermore, different shapes would have different numbers of vertices.
Also, a square consists of four corners where the meeting of the pair of lines takes place. Hence, a square has four vertices. Moreover, a triangle has three vertices and a square pyramid has five.
Edges refer to the lines which join to form the vertices. Furthermore, the outline of a shape is made up by the edges. Also, the creation of an edge takes place when two vertices are joined by a line.
This matter can be somewhat confusing. This is because, in some two-dimensional shapes, there will be only as many vertices as there are edges.
A square certainly has four edges and four vertices. On the other hand, a triangle comprises of three vertices and edges. A square pyramid has a different number of edges and vertices.
Also Check: Holt Geometry Textbook Answers
In Mathematics The Largest Question Youll Probably Have Is What Does Coordinate Mean
Within this guide well attempt to describe what this means and how it is employed in math.
Coordinate is a procedure for translating a pair of coordinates. A few examples of coordinate are translating coordinates which are in relation to meters into the ones which are in terms of feet. They include translating one set of coordinates and translating one set of coordinates.
Coordinate can be of a website that writes essays for you two kinds. 1 kind of coordinate is called in, which stands for the x-direction or the x-axis. The other kind of coordinate is y, which stands for the y-direction or its y-axis. Lets go over these two sorts of coordinate.
For instance, the coordinate is generally used with the y and x axes. The x axis points at the very top and the y axis points.
In math coordinate might be used to tell the length of a lineup. Coordinate may also be used to inform the direction that the line is going, in addition to the number of amounts that it is currently going around the circle, called radians.
Coordinate can be used to measure distance force, mass, stress, or quantities. You can use coordinate to describe the areas of polygons, and the angles between the vertices. This is referred to.
The surface of a space is also referred to. What does coordinate mean in this circumstance?
An orthogonal projection is exactly what it seems like. It refers to a plane in space. Thus, what does discriminate imply at a plane?
Vertices In Computer Graphics
In computer graphics, objects are often represented as triangulated polyhedra in which the object vertices are associated not only with three spatial coordinates but also with other graphical information necessary to render the object correctly, such as colors, reflectance properties, textures, and surface normal these properties are used in rendering by a vertex shader, part of the vertex pipeline.
Read Also: Ccl4 Vsepr Shape
Vertices Faces And Edges
Vertices, Faces and Edges are the three properties that define any three-dimensional solid. A vertex is the corner of the shape whereas a face is a flat surface and an edge is a straight line between two faces. 3d shapes faces, edges and vertices, differs from each other.
In our day-to-day life activities, we come across a number of objects of different shapes and sizes. There are golf balls, doormats, ice-cream cones, coke cans and so on. These objects have different characteristic properties such as length, breadth, diameter, etc., which set them apart from one another. But no matter how different their dimensions are, all of them occupy space and have three dimensions. So they are referred to as three-dimensional Shapes or solids.
There are figures that can be represented on a plane and have 2 dimensions, length, and breadth. And they are referred to as two-dimensional or plane figures. In this article, we will discuss the faces, edges and vertex meaning in Maths for the solid objects.
Chambers 20th Century Dictionaryrate This Definition:
Graph
graf, n. a representation by means of lines, exhibiting the nature of the law according to which some phenomena vary: -graph is used as a terminal in many Greek compounds to denote an agent which writes, & c., as telegraph, seismograph, or the thing written, as in autograph, & c.âadjs.Graphâ²ic, –al, pertaining to writing, describing, or delineating: picturesquely described: vivid.âadv.Graphâ²ically.âns.Graphâ²icness Graphiolâ²ogy, the science or art of writing or delineating, or a treatise thereon Graphâ²is, a genus of lichens, remarkable for the resemblance which the fructification assumes to the forms of the letters of Oriental alphabets Graphâ²Ä«te, a mineral, commonly called blacklead or plumbago , largely used in making pencils.âadj.Graphitâ²ic.âns.Graphâ²ium, a stylus Grapholâ²ogy, the science of estimating character, & c., from handwriting.âGraphic arts, painting, drawing, engraving, as opposed to music, sculpture, & c. Graphic granite, a variety of granite with markings like Hebrew characters.
Read Also: 4 Goals Of Psychology Example
What Does Equidistant Mean In Maths
Equidistantequidistantequidistant
. Accordingly, what is equidistant math?
Equidistant pointsDefinition: A point P is equidistant from others if it is the same distance from them. A point is equidistant from other points if the line segments linking it to them are congruent .
Secondly, what is a synonym for equidistant? d?s t?nt, ?k w?-
In this way, what is the equidistant formula?
For example, consider the line segment containing the end points A and B and midpoint P. These points are said to be equidistant if the distance between the point A and P is equal to the distance between the point P and B, that means the point P is the mid point of A and B.
How do you find equidistant from 3 points?
In other words, it is the point that is equidistant from all three vertices. The circumcenter is constructed in the following way. Again, find the midpoints of the sides of the triangle. Next, construct the perpendicular line to the side that passes through the midpoint of each side.
Common Mathematical Symbols And Terminology Skillsyounee
What does this mean for you? All of the SL program is part of the HL, unlike how the current Group 5 courses, but similar to IB sciences. So, if you decide to pursue HL and then drop down to SL at a later date, provided your school permits this, you can do so without having to backfill the syllabus What does this mean for the other values? if x = 1, then y must be 2, z It would be tempting to define the valence or degree of the vertices in the graph in Figure 10 as the number of edges at a vertex. However, when one does this, it is not true that the sum of the valences of the vertices of the graph adds to twice the number of edges. In math, a function is a relationship between different mathematical quantities. A simple one might look like this: y = 2x. The Riemann zeta function follows the same basic principles The definition of congruent angles is two or more angles with equal measures in degrees or radians. Congruent angles need not face the same way or be constructed using the same figures . If the two angle measurements are equal, the angles are congruent. If angle B a n g l e B and angle D a n g l e D have the same. A Maths Dictionary for Kids is an online math dictionary for students which explains over 955 common mathematical terms and math words in simple language with definitions, detailed visual examples, and online practice links for some entries
Read Also: Sample Space Definition Math
What Is The Vertex Of A Parabola
When we graph a quadratic equation, we get a parabola.
The vertex definition of a parabola is the point where exactly it turns.
It is also called the minimum point.
When the parabola , opens down the vertex is called the maximum point.
The parabola vertex lies at the axis of symmetry.
In the standard form, we write the quadratic equation as \
In the standard form, the vertex of the parabola is given by:
| \ |
where D is the discriminant. \
The vertex equation of a parabola is of the form \^2 + k\)
The vertex of the parabola is at the coordinate
| Vertex of the parabola |
Example 1
Graph of \ = 1 – 2x -3\) is as shown below . Find the vertex of the parabola.
Solution
The coordinates of the vertex are.
Note that the parabola will open downward is negative), but the vertex has a positive y-coordinate.
| \ Vertex of the parabola is at \ |
Example 2
Find the vertex of the parabola \^28\)
Solution
We know that
The vertex equation of a parabola is of the form \^2 + k\) where is the vertex.
In the given equation, h = 3 and k = – 8
Therefore the vertex of the parabola is
| \ Vertex V of the parabola is at |
Reflections Across The Line Y = X
A reflection across the line y = x switches the x and y-coordinates of all the points in a figure such that becomes .
Triangle ABC is reflected across the line y = x to form triangle DEF. Triangle ABC has vertices A , B and C . Triangle DEF has vertices D , E , and F . All of the points on triangle ABC undergo the same change to form DEF.
Also Check: Draw The Lewis Structure For Ccl4.
How Do Vertices Faces And Edges Relate To Other Areas Of Maths
Students will use the knowledge of vertices, faces and edges when looking at 2d shapes as well as 3d shapes. Knowing what edges are and identifying them on compound shapes is crucial for finding the perimeter and area of 2d compound shapes. It is an important foundation for later years when dealing with different maths theorems, such as graph theory and parabolas.
Vertices Faces And Edges Of Common 3d Shapes
How many faces, edges and vertices does a cuboid have?
A cuboid has 8 vertices.
A cuboid has 12 edges.
A cuboid has 6 faces.
How many faces, edges and vertices does a cylinder have?
A cylinder has 0 vertices.
A cylinder has 2 edges.
A cylinder has 2 faces and 1 curved surface.
How many faces, edges and vertices does a hemisphere have?
A hemisphere has 0 vertices.
A hemisphere has 1 curved edge.
A hemisphere has 1 face and 1 curved surface.
How many faces, edges and vertices does a cone have?
A cone has 1 vertex.
A cone has 1 edge.
A hemisphere has 1 face and 1 curved surface.
How many faces, edges and vertices does a tetrahedron have?
A tetrahedron has 4 vertices.
A tetrahedron has 6 edges.
A tetrahedron has 4 faces.
How many faces, edges and vertices does a sphere have?
A sphere has 0 vertices.
A tetrahedron has 0 edges.
A tetrahedron has 1 curved surface.
How many faces, edges and vertices does a prism have?
A prism is a solid object, geometric shape or polyhedron where the faces of both ends are the same shape. As such, students will come across many types of prisms throughout their schooling. Common ones include cubes, cuboids, triangular prisms, pentagonal prisms and hexagonal prisms.
| Shape |
|---|
| 12 |
Read Also: Open Sentence Definition Math