What Is Sum In Math

Sum Of Integers Formula

Before learning the sum of integers formula, let us recall what are integers. Numbers without fractional or decimal components are integers. The sum of integers can be calculated by doing simple mathematics when the numbers to be added are less. But if it is required to add many consecutive integers at a time, we use the sum of integers formula. It simplifies our calculations involved and minimizes our time of addition.

What Is The Geometric Sum Formula

The geometric sum formula is defined as the formula to calculate the sum of all the terms in the geometric sequence. There are two geometric sum formulas. One is used to find the sum of the first n terms of a geometric sequence whereas the other is used to find the sum of an infinite geometric sequence.

How To Estimate A Sum To The Nearest Hundred

To estimate a sum to the nearest hundred, we will take the same steps with some changes:STEP 1: We round the summands to the nearest hundred.STEP 2: We add the rounded numbers.STEP 3: We look at the total amount of rounding, three things can happen:

• If weve rounded one value up and one down, the sum we have obtained is a correct estimation.
• If both summands have been rounded up and the amount of rounding is greater than 50, we subtract 100 from the estimate.
• If both summands have been rounded down and the amount of rounding is greater than 50, we must add 100 to the estimate.

Lets look at an example:

STEP 1: We round the summands.

STEP 2: We add the rounded numbers.

STEP 3: We look at the total amount of rounding.

We have rounded both numbers up. The amount of rounding is 13 +45 =58

Because 58 is greater than 50, we should subtract 100 from the result:

It was very easy, right? The next time you need to estimate sums, remember the advice that we have given you today. And remember that you can find exercises to practice this on Smartick! If you have not done so, sign up and use the Smartick free trial.

Learn More:

Don’t Miss: Who Is Paris Jackson’s Mom

Why Does The Formula Work

Let’s see why the formula works, because we get to use an interesting “trick” which is worth knowing.

First“S”NextSr

Notice that S and S·r are similar?

Now subtract them!

Wow! All the terms in the middle neatly cancel out.

S S·r = a arn

Let’s rearrange it to find S:

Saa

Which is our formula :

So what happens when n goes to infinity?

We can use this formula:

But be careful:

r must be between 1 and 1

and r should not be 0 because the sequence is not geometric

So our infnite geometric series has a finite sum when the ratio is less than 1

Let’s bring back our previous example, and see what happens:

Sum Of First N Natural Numbers

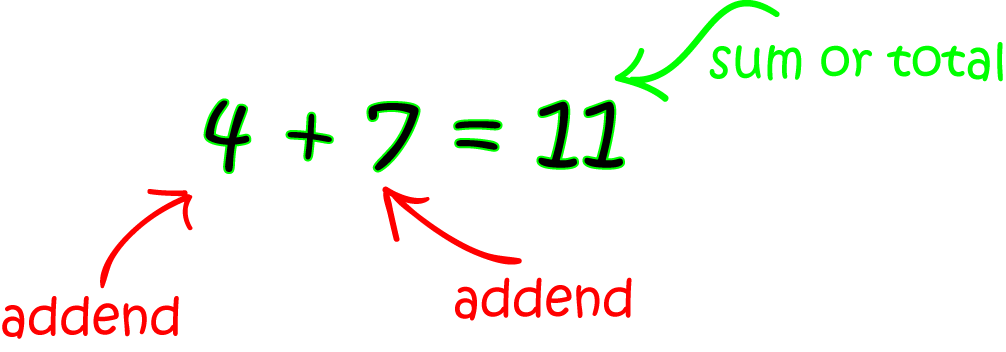
As we know, a sum is the result of summation or the addition of a sequence of numbers. Thus, we can find the sum of the sequence of first n natural numbers.

First n natural numbers are:

1, 2, 3, 4,., n

This is an AP with first term a = 1 and last term l = n.

We know that, the sum of n terms of AP when the first and last terms are known is given by:

Therefore, the formula for sum of even numbers is n.

Read Also: Beth Thomas Documentary

How To Find The Product And Sum Of Two Numbers

Read on for an easy explanation of these concepts, along with helpful examples.

If you are asked to work out the product of two or more numbers, then you need to multiply the numbers together. If you are asked to find the sum of two or more numbers, then you need to add the numbers together.

Below, we will work through several examples together.

In a Nutshell

Derivation Of Geometric Sum Formula

The sum of a geometric series Sn, with common ratio r is given by: \ = \\). We will use polynomial long division formula.

• The sum of first n terms of the Geometric progression is
• \ =a + ar + ar2 + ar3 + … + arn2 + arn1 ————>
• Multiplying both sides by r, we get
• r\ =ar + ar2 + ar3 + … + arn2 + arn1 + arn ————>
• gives r\ -\ = arn- a
• \ = a
• Thus we derive at the sum of n terms of GP as \}\)

Let us see the applications of the geometric sum formulas in the following section.

Break down tough concepts through simple visuals.

Read Also: How To Convert In Chemistry

Implementation In Idris For Sum

Idris>  :let M = Either Integer StringIdris>  MEither Integer String : TypeIdris>  the M Left 4 : Either Integer StringIdris>  :let m = the M Idris>  mLeft 4 : Either Integer String

lookup_default : Nat ->  List a ->  a ->  alookup_default i xs def = case list_lookup i xs of                              Nothing =>  def                              Just x =>  x

What Are The Product And Sum Of 2 4 And 9

Work out the product of 2, 4 and 9.

The product means that you need to multiply the three numbers together.

2 × 4 × 9 = 72

The sum means that you need to add the three numbers together.

2 + 4 + 9 = 15

Question: What do you get if you double 15?

Answer: Just multiply the number by 2 to give 30.

Question: Can you find two numbers which have a product of 12 and a sum of 7?

Answer: 4 and 3 are a the answers.

4 multiplied by 3 is 12. 4 add 3 is 7.

Question: what is the sum and product of -5 and -12?

Answer: Sum means you need to add the numbers .

Product means you need to multiply the numbers .

Question: What is the sum of 8, 2 and 7?

Answer: 8 times 2 is 16, and 16 times 7 is 112.

Question: What is the product of 3 and 154?

Answer: To find the product multiply the two numbers together to give 462.

Question: What number is 36 less than twice the product of 88 and 11?

Answer: First work out the product of 88 and 11 by multiplying 88 by 11 to give 968.

Now work out 968 minus 36 which is 932.

Question: Find 45 less than the product of 7 and 9?

Answer: The product of 7 and 9 is 7 times 9 which is 63.

Now work out 63 take away 45 to give 18.

Question: The sum of two numbers is 9 and their difference is 3. What is their product?

Answer: First find out what the two numbers are.

These are 6 and 3, since 6 add 3 is 9, and 6 minus 3 is 3.

Now multiply 6 by 3 to give 18.

Question: What are the two numbers which have a sum and product of 1 and 9?

Now multiply 15 and 11 to give 165.

Also Check: Colorful Overnight Geometry Dash

Sum Of The Squares Of The First N

Continuing the idea from the previous section, start with the binomial expansion of (

^3 = k^3 – 3k^2 + 3k – 1. 3=k33k2+3k1.

Rearrange the terms:

k^3-^3=3k^2-3k+1. k33=3k23k+1.

As before, summing the left side from k

6 . \beginn^3 & = 3 \left – 3 \sum_^n k + \sum_^n 1 \\n^3 & = 3 \left – 3 \frac2 + n \\3 \left & = n^3 + 3 \frac2 – n \\\Rightarrow \sum_^n k^2 & = \frac13 n^3 + \frac12 n^2 + \frac16 n \\& = \frac6.\end n3n33k=1nk2=33k=1nk+k=1n1=332n+n=n3+32nn=31n3+21n2+61n=6n.

Find the sum of the squares of the first 100

4 . \begin4s_ & = n^4 + 6 \frac6 – 4 \frac2 + n \\\\s_ & = \frac14 n^4 + \frac12 n^3 + \frac34 n^2 + \frac14 n – \frac12 n^2 – \frac12 n + \frac14 n \\\\s_ & = \frac14 n^4 + \frac12 n^3 + \frac14 n^2 \\\\& = \frac4.\end 4s3,ns3,ns3,n=n4+66n42n+n=41n4+21n3+43n2+41n21n221n+41n=41n4+21n3+41n2=4n22.

Find the sum of the cubes of the first 200

\begin1^2+3^2+5^2+\cdots+^2& =\left^2+^2\right)-\left^2\right)\\& =\sum_^ i^2-\sum_^^2\\& =\frac-\frac\\& =\frac\\& =\frac.\ _\square\end 12+32+52++2=2+2)2)=i=12ni2i=1n2=62n32n=3n2)=3n.

How To Understand Sum Symbol

I have searched google for an answer but I’m not sure what I’m asking. I know that Sigma means sum but there is an ‘n’ above Sigma and an ‘i=1’ under sigma. how can i understand this? thank you!

• 2$\begingroup$Shorthand notation for “$a_1+a_2+\cdots+ a_n$” is “$\sum\limits_^n a_i$”. You would read that summation symbol as “the sum from $i=1$ to $n$ of $a_i$”.$\endgroup$Aug 27, 2013 at 15:16
• $\begingroup$Ok so it’s just a counting sequence!$\endgroup$Aug 27, 2013 at 15:18
• 1$\begingroup$@DavidMitra I know what you mean, but just so this doesn’t go without saying, it’s $a_1+a_2+\ldots +a_n$ that is short for $\sum \limits_^na_n$.$\endgroup$ Git GudAug 27, 2013 at 15:20

Don’t Miss: Is Paris Jackson Michaels Biological Daughter

Learn How To Estimate A Sum With Examples

• Category:

In this post, we will learn to estimate a sum.

Do you know what estimating a sum can help us with? When we have to do an operation mentally, often we do not need the exact result but an estimate of the outcome.Other times, after we have done an operation on paper and want to verify that the amount we got is reasonable, an estimate of the sum also helps us.It is quite useful, right? Today we will show you some very simple steps to learn how to estimate a sum.

Direct Sum In Categories

An additive category is an abstraction of the properties of the category of modules. In such a category, finite products and coproducts agree and the direct sum is either of them, cf. biproduct.

General case:In category theory the direct sum is often, but not always, the coproduct in the category of the mathematical objects in question. For example, in the category of abelian groups, direct sum is a coproduct. This is also true in the category of modules.

Direct sums versus coproducts in category of groups

However, the direct sum

Don’t Miss: Prince Jackson Biological Father

Sum Of Three Digit Numbers

Now, go through the process of finding the sum of three-digit numbers given below:

Step 1: Write the given numbers in the column by providing enough space between digits for easy understanding.

Step 2: Add the ones place digits together, transfer the carry . Finally, it gives the sum of numbers that are in the unit place.

Step 3: Add the tens place digits and carry from the previous step and transfer the carry. It gives the sum of numbers in the tens place.

Step 4: Add the digits in hundreds place digits, and carry the number from the previous step . Thus, it provides the hundreds or thousands or both of the result.

Step 5: Thus, the digits in the final row represent the sum of given numbers.

Similar procedure can be applied to find the sum of large digit numbers. Lets have a look at the example given below.

Example: Find the sum of 673 and 492.

What Is The Sum Or Autosum Icon And Its Function

In most spreadsheet programs, the Sum feature is represented by a Sigma icon. In Microsoft Excel, the AutoSum or Sum icon and function allows you calculate a total for the values of selected cells quickly. When using Sum, the calculated total is displayed below the last selected cell in a column or to the right of the last selected cell.

The AutoSum and Sum functions are on the Home tab of the Excel Ribbon, in the Editing section.

Read Also: Holt Mcdougal Geometry: Practice And Problem Solving Workbook Answer Key

Addition Using Simpler Sums

When trying to find the sum of multiple numbers, or larger numbers, it is helpful to remember the properties of addition. In particular, the commutative and associative properties of addition allow us to move numbers around and group them in ways that allows us to more easily add them.

The commutative property of addition says that 1 + 3 = 3 + 1 = 4. The order in which we add doesn’t matter.

The associative property of addition says that + 10 = 1 + = 13, so it doesn’t matter whether we add 1 and 2 first, or 2 and 10 first. The result is the same.

It can sometimes be helpful, especially when first learning addition, to break numbers apart into numbers we may be more comfortable with.

Example

27 + 41 = ?

If we aren’t yet comfortable with addition using columns and carrying, we could break each digit in the above problem up into a sum of smaller numbers, then rearrange and group them using properties of addition.

27 = 20 + 7 = 10 + 10 + 5 + 2

41 = 20 + 20 + 1 = 10 + 10 + 10 + 10 + 1

Now that we have broken up the problem into 10s, 5s, 2s, and 1s, this should make it easier to find the sum:

10 + 10 + 10 + 10 + 10 + 10 = 60

5 + 2 + 1 = 8

What Is A Sum

The sum of two numbers is the answer you get when you add them both together. So the sum of 5 and 4 is 9.

There was a time when teachers used the word ‘sum’ to name the following addition number sentence:

9 + 5 = 14

They would often then mistakenly use the same word to name these subtraction, multiplication and division number sentences:

9 – 4 = 57 x 3 = 2180 ÷ 10 = 8

To get round this confusion, we now refer to all of the above as number sentences.

Also Check: Algebra 2 Parcc

What Is The Geometric Sum Formula In Math

In math, the geometric sum formula refers to the formula that is used to calculate the sum of all the terms in the geometric sequence. The two geometric sum formulas are:

• The geometric sum formula for finite terms: If r = 1, Sn = an and if r1,Sn=a/1r
• The geometric sum formula for infinite terms: Sn=a1r. If |r| < 1 , S = a/

What Could Be The Sum

A Lesson with Third Graders

Itsimportanttomakeconnectionsamongthedifferentareasofmathematics,andthislessonpresents anadditionprobleminageometriccontextthatisappropriateforthirdgraders.Theproblemalsois goodforsupportingmentalcomputationandforgivingchildrenexperiencewithamathproblemthat hasmorethanonesolution.TheideaforthelessoncomesfromPeterSullivanandPatLilburnsbook, Good Questions for Math Teaching: Why Ask Them and What to Ask, K6, aresourcethatonregularlywhenplanningnewlessons.taughtthislessontothirdgradersatPark SchoolinMillValley,California.

As the third graders watched, I drew on the board a sketch of a cube with three faces showing, labeled with 7,8,and 9.Its three-dimensional, Purna commented.

The faces of this cube are numbered consecutively, I said and then asked,Who knows what consecutively means? No one had an idea.

It means that the numbers go in order, I explained. When we count, we count with consecutive numbers, like seven, eight, nine. I wrote on the board:

But seven, ten, and two are not consecutive numbers, I said. Theyre not in order. This seemed to be clear to the children. I also thought that facewas new terminology for them when referring to a cube, but I thought that its meaning was clear from the context. I thought Id raise another question about cubes.

I think seven, she said.

Tell me how you were thinking, I said to Audrey, holding her eyes with my gaze and ignoring the protests from some of the other students.

Don’t Miss: Unit 2 Formative Assessment Common Core Algebra 2 Answer Key

Definition Of The Summation Symbol

The symbol `\sum` indicates summation and is used as a shorthand notation for the sum of terms that follow a pattern.

For example, the sum of the first 4 squared integers, `1^2+2^2+3^2+4^2,` follows a simple pattern: each term is of the form `i^2,` and we add up values from `i=1` to `i=4.` We can write the sum compactly with summation notation as \Similarly, \We don’t have to use $i$ for the index, we could use another variable, like $j$:\begin \sum_^2 \frac & = \frac + \frac + \frac + \frac + \frac\\& = 1 + \frac + \frac + \frac + \frac\end

In general, we define the sum as:\

Cite this as

How To Estimate A Sum To The Nearest Tenth

To estimate an amount to the tenth we have 3 steps to follow:STEP 1: We round the summands to the nearest tenth. Remember:

• If the number ends in 0, 1, 2, 3 or 4, we round down
• If the number ends in 5, 6, 7, 8 or 9, we round up

STEP 2: We add the rounded numbersSTEP 3: We look at the total amount of rounding. three things can happen:

• If weve rounded one amount up and one down, the sum we have obtained is a correct estimation.
• If both summands have been rounded up and the amount of rounding is greater than 5, we subtract 10 from the estimate.
• If both summands have been rounded down and the amount of rounding is greater than 5, we add 10 to the estimate.

Lets look at an example for each of these three cases:

Example 1

• STEP 1: Round the summands.

• STEP 2: Add the rounded numbers.

• STEP 3: Look at the total amount of rounding. We have rounded one number down and the other up:

The estimate is correct.

STEP 1: Round the summands.

STEP 2: Add the rounded numbers.

STEP 3: Look at the total amount of rounding.

We have rounded the two summands down. The amount rounded is 2 + 4 = 6.

As 6 is greater than 5, we must add 10 to the estimate:

Example 3

STEP 1: Round the summands.

STEP 2: Add the rounded numbers.

STEP 3: Look at the total amount of rounding.

We have rounded the two summands up. The amount of rounding is 3 + 1 = 4. As 4 is less than 5, the estimate is correct:

Don’t Miss: Does Quantum Physics Prove God

What Is The Sum Of Two Numbers

The sum of two numbers is just putting two numbers together.

Finding the sum of small numbers is not hard.

You can use your fingers to add.

Let’s look at an example to understand how to add numbers using our fingers.

Alaya is standing near a traffic signal.

She is trying to count the number of vehicles that have stopped at the red light signal.

She sees three buses at the signal.

She counts them by opening three fingers of one hand.

Next, she sees two more buses that have stopped at the signal.

She counts them by opening two more fingers.

Now, Alaya counts all the fingers opened in her hand to count the number of buses at the signal.

There are five open fingers which means that there are 5 buses at the signal.

Now, let’s see how to find a sum using a number line.

We will find the sum of 3 and 2 using a number line.

First, draw a number line and encircle the first addend 3 on it.

Now, make two jumps to the right of 3

The number you reach is 5

This is the sum.