What Is Negative Acceleration
Acceleration of a body is negative if the velocity of the body decreases.The direction of negative acceleration is opposite to the direction in which the body is moving. Negative acceleration is also called deceleration or retardation.
Examples of negative acceleration
- When a train reaches a station its velocity decreases with time, this type of acceleration is called negative acceleration.
similarly:In example, an elevator moving upward cane accelerate upward with positive acceleration and move faster or accelerate downward with negative acceleration and move slower.When it is moving downward with negative velocity, it can accelerate downward with negative acceleration and move slower. When the acceleration and velocity have positive signs, so that the speed is decreasing, we refer to a deceleration.How do you calculate the acceleration due to gravity?The acceleration of freely falling bodies is called gravitational acceleration.Drop an object from some height and observe its motion.Does its velocity increase,decrease or remain constant as it approaches the ground? Galileo was the first scientist to notice that all the freely falling objects have the same acceleration independent of their masses.
How Do You Find The Time It Takes To Reach Maximum Height Of A Projectile
Determine the time it takes for the projectile to reach its maximum height. Use the formula / -32.2 ft/s^2 = T where V is the initial vertical velocity found in step 2. In this formula, 0 represents the vertical velocity of the projectile at its peak and -32.2 ft/s^2 represents the acceleration due to gravity.
What Is Uniform Acceleration
We know that acceleration is the rate of change of velocity with respect to time. Acceleration is a vector quantity and the direction of acceleration will be the same as the direction of the rate of change of velocity. The SI unit of acceleration is m/s2 and the dimensions of acceleration are .
We are familiar with the concept of uniform motion, if an object covers equal displacement in an equal interval of time it is said to be undergoing uniform motion. Now the question is what is meant by uniform acceleration?
Don’t Miss: Find The Length Indicated Geometry Worksheet Answers
Kinematic Equations Of Constant Acceleration
In this article you’ll learn how to derive equations of straight line motion based on constant acceleration. It means these equations are valid only when the acceleration is constant and we call them kinematic equations for constant acceleration. An example of constant acceleration motion is freely falling bodies under the action of gravity neglecting the air resistance.
How The Kinematic Equations Are Related To Acceleration

We are studying concepts related to motion: time, displacement, velocity, and especially acceleration. We are only concerned with motion in one dimension. The kinematic equations apply to conditions of constant acceleration and show how these concepts are related. Constant acceleration is acceleration that does not change over time. The first kinematic equation relates displacement d, average velocity v
According to this equation, a graph of velocity squared versus twice the displacement will have a slope equal to acceleration.
Note that, in reality, knowns and unknowns will vary. Sometimes you will want to rearrange a kinematic equation so that the knowns are the values on the axes and the unknown is the slope. Sometimes the intercept will not be at the origin . This will happen when v0 or d0 is not zero. This will be the case when the object of interest is already in motion, or the motion begins at some point other than at the origin of the coordinate system.
Recommended Reading: What Is An Example Of Movement In Geography
Example 5 Calculating Displacement: How Far Does A Car Go When Coming To A Halt
On dry concrete, a car can decelerate at a rate of 7.00 m/s2, whereas on wet concrete it can decelerate at only 5.00 m/s2. Find the distances necessary to stop a car moving at 30.0 m/s on dry concrete and on wet concrete. Repeat both calculations, finding the displacement from the point where the driver sees a traffic light turn red, taking into account his reaction time of 0.500 s to get his foot on the brake.
Strategy
Draw a sketch.
Figure 9.
In order to determine which equations are best to use, we need to list all of the known values and identify exactly what we need to solve for. We shall do this explicitly in the next several examples, using tables to set them off.
Solution for
1. Identify the knowns and what we want to solve for. We know that v0 = 30.0 m/s v = 0 a = -7.00 m/s2 . We take x0 to be 0. We are looking for displacement x, or xx0.
2. Identify the equation that will help up solve the problem. The best equation to use is
This equation is best because it includes only one unknown, x. We know the values of all the other variables in this equation.
3. Rearrange the equation to solve for x.
4. Enter known values.
Thus,
x
Solution for
This part can be solved in exactly the same manner as Part A. The only difference is that the deceleration is 5.00 m/s2. The result is
x
Solution for
1. Identify the knowns and what we want to solve for. We know that \bar=30.0 \text treaction = 0.500 s areaction = 0. We take x0-reaction = to be 0. We are looking for xreaction.
Solved Examples On Acccerelation Formula
Question- A woman is traveling by her sports car at a constant velocity v = 5.00 m/s. When she steps on the gas, it makes the car to accelerate forward. Further, past 10.0 seconds, she stops the acceleration and continues a constant velocity v = 25.0 m/s. Calculate the acceleration of the car.
Answer- In the forward direction, initial velocity is \ = 5.00 m/s. Further, the final velocity in the forward direction is \ = 25.0 m/s. The time in which the change took place is 10.0 s. Therefore, the acceleration is in the forward direction, with a value:
a = \
a = \
a = \
a = 2.00 m/s2
Therefore, we see that the acceleration of the car is 2.00 m/s2 forward.
Question- A man takes a rock and drops it off from a cliff. It falls for 15.0 s before it hits the ground. The acceleration due to gravity g = 9.80 m/s2. Calculate the velocity of the rock the moment before it had hit the ground.
Answer- The man released the rock from rest, therefore, we get the initial velocity as \ = 0.00 m/s. The time for the change to take place is 15.0 s. The acceleration for this is 9.80 m/s2. Therefore, to find the velocity we will rearrange the equation like:
a = \ + at
\ + at
\ = 0.00 m/s +
\ = 147 m/s
Therefore, as the rock is falling, the direction of the velocity is down.
Don’t Miss: Exponential Modeling With Percent Growth And Decay Common Core Algebra 2 Homework
What Is Average Acceleration In Physics
The average acceleration of a body given in the above equation is a during time t. Let the time t is divided into many smaller intervals of time. If the rate of change of velocity during all these intervals remains constant then the acceleration also remains constant. Such a body is said to possess uniform acceleration.
average acceleration formula
Example: Find Time Given Final Velocity Initial Velocity And Acceleration
A car approaching a school zone slows down from 27 m/s to 9 m/s with constant acceleration -2 m/s2.
How much time is required to slow down to final velocity?
Answer: We know initial velocity , velocity and acceleration
We first need to solve the velocity equation for time :
v = u + at
Plugging in the known values we get, t = /a t = / -2 m/s2 t = -18 m/s / -2 m/s2 t = 9 s
Recommended Reading: Geometry Segment Addition Postulate Worksheet
Example 2 Calculating Final Velocity: An Airplane Slowing Down After Landing
An airplane lands with an initial velocity of 70.0 m/s and then decelerates at 1.50 m/s2 for 40.0 s. What is its final velocity?
Strategy
Draw a sketch. We draw the acceleration vector in the direction opposite the velocity vector because the plane is decelerating.
Figure 4.
1. Identify the knowns. v0 = 70.0 m/s, a = 1.50 m/s2, t = 40.0 s.
2. Identify the unknown. In this case, it is final velocity, vf.
3. Determine which equation to use. We can calculate the final velocity using the equation v=_+.
4. Plug in the known values and solve.
Discussion
The final velocity is much less than the initial velocity, as desired when slowing down, but still positive. With jet engines, reverse thrust could be maintained long enough to stop the plane and start moving it backward. That would be indicated by a negative final velocity, which is not the case here.
Figure 5. The airplane lands with an initial velocity of 70.0 m/s and slows to a final velocity of 10.0 m/s before heading for the terminal. Note that the acceleration is negative because its direction is opposite to its velocity, which is positive.
In addition to being useful in problem solving, the equation v=_+\text gives us insight into the relationships among velocity, acceleration, and time. From it we can see, for example, that
Charged Particle In An Electromagnetic Field
One of the fundamental forces of nature, the electromagnetic force, consists of the electric and the magnetic field. On one hand, the electric field always acts on the charged particle, and on the other hand, the magnetic field acts only when this particle is moving.
The magnitude of force F which is exerted on the charged particle in the electric field E can be described with the Coulomb’s law. It states that F = q * E, where q is the charge of the particle. You can see that particles with the higher charge will always be attracted stronger.
Read Also: Paris Jackson Real Parents
Magnitude Of Acceleration Calculator
Welcome to our magnitude of acceleration calculator – a fantastic tool that knows how to find the magnitude ofacceleration. But that’s not the end of the story. Read the article to learn:
- What does acceleration mean?
- Is there a single magnitude of acceleration formula?
- How to find the acceleration from the velocity difference?
If you’ve asked yourself one of these questions recently , this is the best place to find the answer!
What Is The Formula For Acceleration And Velocity
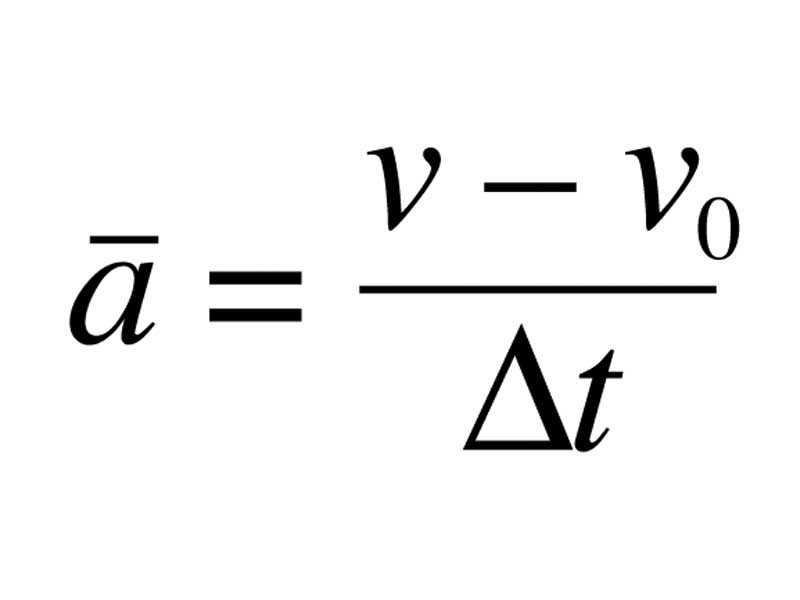
| Position from velocity and acceleration | x=x0+v0t+12at2 |
Also, What is the symbol for final velocity?
The symbol v is the velocity some time t after the initial velocity. It is often called the final velocity but this does not make it an objects last velocity.
| t |
Hereof, What is the relation between velocity and acceleration?
Velocity is the rate of change of position with respect to time, whereas acceleration is the rate of change of velocity. Both are vector quantities , but the units of velocity are meters per second while the units of acceleration are meters per second squared.
Also to know Can initial velocity be zero? When a body starts from rest or it changes it direction of motion,it is called as initial velocity. We generally consider initial velocity is equal to zero,only when the object starts from rest. Generally at time ,the initial velocity is zero.
Is V initial or final velocity?
It is represented by letter u. Three initial velocity formulas based on equations of motion are given below, If time, acceleration and velocity are known. The initial velocity is formulated as.
24 Related Questions Answers Found
Also Check: Lesson 4.5 Practice B Geometry Answers
Solving For Final Position When Velocity Is Not Constant
We can combine the equations above to find a third equation that allows us to calculate the final position of an object experiencing constant acceleration. We start with
Adding v0 to each side of this equation and dividing by 2 gives
Since \frac_+v}=\bar for constant acceleration, then
Now we substitute this expression for \bar into the equation for displacement, x=_+\bart, yielding
How To Find The Magnitude Of Acceleration
There are a few ways to estimate the magnitude of acceleration. We implement three of them in this magnitude of acceleration calculator:
According to Newton’s second law, the acceleration a is proportional tothe net forceF and inversely proportional to the object’smassm. So how to calculate the magnitude of acceleration? By analogy – the magnitude of the acceleration is proportional to the magnitude of this force. Let’s convert these words to the magnitude of acceleration formula:
|a| = |F| / m.
Here, bolded symbols represent vectors, and vertical lines denote a vector’s magnitude, the absolute value, which is always positive .
As acceleration is a vector, we can always get this quantity by summing up the acceleration’s components. We can use a simple addition of vectors. In general, for two components, we can write:
a = a1 + a2.
In the Cartesian plane, we can use x- and y-coordinates , and if we are working with a circular motion, it’s worth implementing tangential and centripetal components .
In either case, you receive a vector. And how to find the magnitude of acceleration? As both components are perpendicular to each other, square the values and work out the square root of the sum:
|a| = .
In three-dimensional space the magnitude of acceleration formula extends to:
|a| = .
Also Check: Geometry Basics Homework 2 Segment Addition Postulate Answer Key
Why Is Final Velocity Zero At Maximum Height
The maximum height of a object in a projectile trajectory occurs when the vertical component of velocity, vy , equals zero. As the projectile moves upwards it goes against gravity, and therefore the velocity begins to decelerate. Once the projectile reaches its maximum height, it begins to accelerate downward.
Applying Kinematic Equations To Situations Of Constant Acceleration
Problem-solving skills are essential to success in a science and life in general. The ability to apply broad physical principles, which are often represented by equations, to specific situations is a very powerful form of knowledge. It is much more powerful than memorizing a list of facts. Analytical skills and problem-solving abilities can be applied to new situations, whereas a list of facts cannot be made long enough to contain every possible circumstance. Essential analytical skills will be developed by solving problems in this text and will be useful for understanding physics and science in general throughout your life.
Problem-Solving Steps
While no single step-by-step method works for every problem, the following general procedures facilitate problem solving and make the answers more meaningful. A certain amount of creativity and insight are required as well.
Recommended Reading: Draw A Lewis Structure (including All Lone Pair Electrons) For The Species Ccl4:
Calculating Acceleration From A Force
Example : Calculating Final Velocity: Dragsters
Calculate the final velocity of the dragster in Example 3 without using information about time.
Strategy
Draw a sketch.
Figure 8.
The equation ^=_^+2a\left is ideally suited to this task because it relates velocities, acceleration, and displacement, and no time information is required.
Solution
1. Identify the known values. We know that v0 = 0, since the dragster starts from rest. Then we note that xx0 = 402 m . Finally, the average acceleration was given to be a = 26.0 m/s2.
2. Plug the knowns into the equation^=_^+2a\left and solve for v.
v
Thus
To get v, we take the square root:
Discussion
145 m/s is about 522 km/h or about 324 mi/h, but even this breakneck speed is short of the record for the quarter mile. Also, note that a square root has two values we took the positive value to indicate a velocity in the same direction as the acceleration.
An examination of the equation ^=_^+2a\left can produce further insights into the general relationships among physical quantities:
- The final velocity depends on how large the acceleration is and the distance over which it acts
- For a fixed deceleration, a car that is going twice as fast doesnt simply stop in twice the distanceit takes much further to stop.
Don’t Miss: How To Find Ksp From Molarity