What Is The Meaning Of Sas In Math

Congruence Of Triangles: Conditions

Content Curator| Updated On -Oct 21, 2022

Congruence of triangles is a property of two triangles. Any two triangles are said to be congruent if all the 3 corresponding sides and angles of triangles are equal in measure. Read this entire article to know about the congruence of triangles, conditions for congruence of two triangles, corresponding parts of congruent triangles and solved examples related to congruence of triangles. Two shapes are said to be congruent if their size and shape are the same. Images of two shapes are in a way that the mirror image of one should coincide with the other.

Two triangles are said to be congruent if their all-corresponding sides and angles are equal.

Sides: AB=BC=AC=PQ=QR=PR

Angles: A=B=C=P=Q=R

So, we can say both triangles ABC and PQR are congruent.

The Sas Congruence Rule

The Side-Angle-Side theorem of congruency states that, if two sides and the angle formed by these two sides are equal to two sides and the included angle of another triangle, then these triangles are said to be congruent.

Verification:

Let’s perform an activity to show the proof of SAS. Given: AB=PQ, BC=QR, and B=Q. To prove: ABC PQR

Place the triangle ABC over the triangle PQR such that B falls on Q and side AB falls along the side PQ.

• Since AB=PQ, so point A falls on point P.
• Since B=Q, so the side BC will fall along the side QR.
• BC=QR, so point C falls on point R. Thus, BC coincides with QR and AC coincides with PR.

So, ABC will coincide with PQR. Therefore, ABCPQR. This demonstrates SAS criterion of congruence.

Technical Overview And Terminology

SAS is a software suite that can mine, alter, manage and retrieve data from a variety of sources and perform statistical analysis on it. SAS provides a graphical point-and-click user interface for non-technical users and more through the SAS language.

SAS programs have DATA steps, which retrieve and manipulate data, and PROC steps, which analyze the data. Each step consists of a series of statements.

The DATA step has executable statements that result in the software taking an action, and declarative statements that provide instructions to read a data set or alter the data’s appearance. The DATA step has two phases: compilation and execution. In the compilation phase, declarative statements are processed and syntax errors are identified. Afterwards, the execution phase processes each executable statement sequentially. Data sets are organized into tables with rows called “observations” and columns called “variables”. Additionally, each piece of data has a descriptor and a value.

The PROC step consists of PROC statements that call upon named procedures. Procedures perform analysis and reporting on data sets to produce statistics, analyses, and graphics. There are more than 300 named procedures and each one contains a substantial body of programming and statistical work. PROC statements can also display results, sort data or perform other operations.

SAS macros are pieces of code or variables that are coded once and referenced to perform repetitive tasks.

You May Like: Is Clinical Psychology In Demand

Rules For Triangle Congruency

Congruent triangles are triangles that have the same size and shape.This means that the corresponding sides are equal and the corresponding angles are equal.

We can tell whether two triangles are congruent without testing all the sides and all the angles ofthe two triangles. In this lesson, we will consider the four rules to prove triangle congruence.They are called the SSS rule, SAS rule, ASA rule and AAS rule.In another lesson, we will consider a proof used for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.

The following diagrams show the Rules for Triangle Congruency: SSS, SAS, ASA, AAS and RHS. Take notethat SSA is not sufficient for Triangle Congruency. Scroll down the page for more examples, solutionsand proofs.

Conditions For Congruence Of Triangles

If there are two triangles A and B then if they fulfil any of the below mentioned conditions then they are said to be congruent and they are mentioned like below:

A\ B

A = 40°

Ques2: What is CPCT?

Ans. CPCT stands for Corresponding Parts of Congruent Triangles. It is a theorem which states that if two or more triangles which are congruent to each other then the corresponding angles and sides are also congruent to each other.

Ques3: Is it possible two equilateral triangles are always congruent?

Ans. No it is not always possible. Equilateral triangle angles are of 60 degrees each but it is noy necessary that their sides are always equal.

Ques4: The length of two sides of an isosceles triangle are 5cm and 8 cm, find perimeter of triangle.

Ans. If we consider two sides of isosceles triangles are 5 cm and third one 8 cm then perimeter will be 5 cm+5 cm+8 cm= 18 cm

Ans. In LMN and ONM

LM=ON

MN=NM

Ans.

Read Also: Geometry Dash Eric Van Wilderman

Comparison To Other Products

In a 2005 article for the Journal of Marriage and Family comparing statistical packages from SAS and its competitors Stata and SPSS, Alan C. Acock wrote that SAS programs provide “extraordinary range of data analysis and data management tasks,” but were difficult to use and learn. SPSS and Stata, meanwhile, were both easier to learn but had less capable analytic abilities, though these could be expanded with paid or free add-ons. Acock concluded that SAS was best for power users, while occasional users would benefit most from SPSS and Stata. A 2014 comparison by the University of California, Los Angeles, gave similar results.

Competitors such as Revolution Analytics and Alpine Data Labs advertise their products as considerably cheaper than SAS’. In a 2011 comparison, Doug Henschen of InformationWeek found that start-up fees for the three are similar, though he admitted that the starting fees were not necessarily the best basis for comparison. SAS’ business model is not weighted as heavily on initial fees for its programs, instead focusing on revenue from annual subscription fees.

Using Two Column Proofs To Prove Triangles Congruent

Triangle Congruence by SSSHow to Prove Triangles Congruent using the Side Side Side Postulate? If three sides of one triangle are congruent to three sides of another triangle, then the two trianglesare congruent.

Triangle Congruence by SASHow to Prove Triangles Congruent using the SAS Postulate? If two sides and the included angle of one triangle are congruent to two sides and the included angle ofanother triangle, then the two triangles are congruent.

Prove Triangle Congruence with ASA PostulateHow to Prove Triangles Congruent using the Angle Side Angle Postulate? If two angles and the included side of one triangle are congruent to two angles and the included sideof another triangle, then the two triangles are congruent.

Prove Triangle Congruence by AAS PostulateHow to Prove Triangles Congruent using the Angle Angle Side Postulate? If two angles and a non-included side of one triangle are congruent to two angles and a non-includedside of another triangle, then the two triangles are congruent.

Also Check: N2h2 Lewis Structure Molecular Geometry

Definition Of Congruence In Analytic Geometry

In a Euclidean system, congruence is fundamental it is the counterpart of equality for numbers. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.

A more formal definition states that two subsetsA and B of Euclidean spaceRn are called congruent if there exists an isometryf : Rn â Rn ) with f = B. Congruence is an equivalence relation.

How Can You Tell If Triangles Are Congruent

You could cut up your textbook with scissors to check two triangles. That is not very helpful, and it ruins your textbook. If you are working with an online textbook, you cannot even do that.

Geometricians prefer more elegant ways to prove congruence. Comparing one triangle with another for congruence, they use three postulates.

Don’t Miss: Definition Of Equilateral Triangle In Geometry

Three Ways To Prove Triangles Congruent

A video lesson on SAS, ASA and SSS.

How Do You Use Sas Congruence Theorem

Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent. The SAS rule states that: If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent. An included angle is an angle formed by two given sides.

Read Also: What Is The Formula Of Area In Physics

What Do You Mean By Side Angle Side

SAS congruence is the term which is also known as Side Angle Side congruence, which is used to describe the relation of two figures that are congruent. Let’s discuss the SAS congruence of triangles in detail to understand the meaning of SAS. Look at ABC and PQR:

These two triangles are of the same size and shape. Thus, we can say that these are congruent. They can be considered as congruent triangle examples. We can represent this in a mathematical form using the congruent triangles symbol . . This means D falls on P, E falls on Q, and F falls on R. ED falls on PQ, EF falls on QR, and DF falls on PR. Thus, we can conclude that the corresponding parts of the congruent triangles are equal.

Triangle Congruence Postulates Sss & Sas Explained W/ 13 Examples

// Last Updated:

Did you know that there are five ways you can prove triangle congruency?

Jenn, Founder Calcworkshop®, 15+ Years Experience

Its true!

In todays geometry lesson, were going to tackle two of them, the Side-Side-Side and Side-Angle-Side postulates.

Youll quickly learn how to prove triangles are congruent using these methods.

In addition, youll see how to write the associated two column proof.

Lets jump in!

So we already know, two triangles are congruent if they have the same size and shape. This means that the pair of triangles have the same three sides and the same three angles .

Thankfully we dont need to prove all six corresponding parts are congruent we just need three!

Why?

Because if we can show specific sides and/or angles to be congruent between a pair of triangles, then the remaining sides and angles are also equal.

But there is a warning we must be careful about identifying the accurate side and angle relationships!

As Math is Fun accurately states, there only five different congruence postulates that will work for proving triangles congruent. So we need to learn how to identify congruent corresponding parts correctly and how to use them to prove two triangles congruent.

You May Like: What Does Anxiety Mean Psychology

Determining Congruence Of Polygons

For two polygons to be congruent, they must have an equal number of sides . Two polygons with n sides are congruent if and only if they each have numerically identical sequences side-angle-side-angle-… for n sides and n angles.

Congruence of polygons can be established graphically as follows:

• First, match and label the corresponding vertices of the two figures.
• Second, draw a vector from one of the vertices of the one of the figures to the corresponding vertex of the other figure. Translate the first figure by this vector so that these two vertices match.
• Third, rotate the translated figure about the matched vertex until one pair of corresponding sides matches.
• Fourth, reflect the rotated figure about this matched side until the figures match.

If at any time the step cannot be completed, the polygons are not congruent.

What Is The Sas Formula

Consider a,b, and c are the different sides of a triangle. Thus, the area of a SAS triangle formula is expressed as, When sides ‘b’ and ‘c’ and included angle A is known, the area of the triangle is: 1/2 × bc × sin When sides ‘b’ and ‘a’ and included angle B is known, the area of the triangle is: 1/2 × ab × sin

Read Also: How To Find Fg Physics

Congruent Meaning In Maths

The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.

Two shapes are congruent if they have the same shape and size. We can also say if two shapes are congruent, then the mirror image of one shape is the same as the other.

Basics To Sss Sas Asa Aas Rules:

Two triangles are congruent if they have:Exactly the same three side and

Exactly the same three angles.

But we dont have to know all three sides and all three angles

..usually three out of six is enough

There are four ways to find if two triangles are congruent: SSS, SAS, ASA and AAS

SSS stands for side, side, side and means that we have two triangles with all three sides equal.

If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.

SAS stands for side, angle, side and means that we have two triangles where we know two sides and the included angle are equal.

If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.

ASA stands for angle, side, angle and means that we have two triangles where we know two angles and the included side are equal.

If two angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

AAS stands for angle, angle, side and means that we have two triangles where we know two angles and the non-included side are equal.

If two angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

You May Like: Why Do I Hate My Birthday Psychology

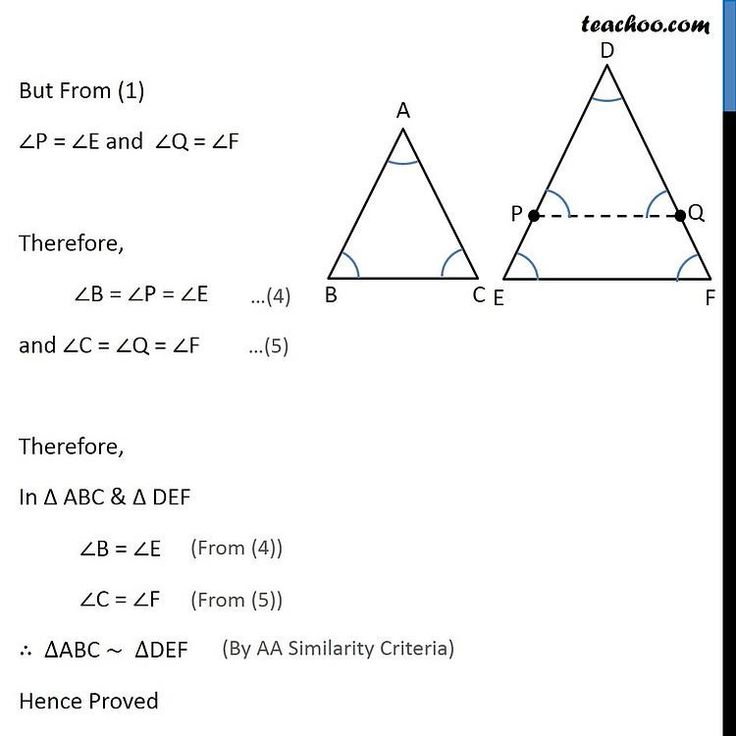
The Sas Similarity Rule

The SAS similarity criterion states that If two sides of one triangle are respectively proportional to two corresponding sides of another, and if the included angles are equal, then the two triangles are similar.

Given: DE/AB=DF/AC and D=A. To prove: DEF is similar to ABCThe SAS criterion tells us that ABC ~ DEF. Let us see the justification of this.

Construction:

• Take a point X on AB such that AX = DE.
• Through X, draw segment XY BC, intersecting AC at Y.

Proof:

Since XY II BC, we can note that AXY ~ ABC, and thus: AX/AB = AY/AC….

Now, we will show that AXY and DEF are congruent. It is given that DE/AB=DF/AC….

Since AX=DE and from and , we have: DE/AB = AX/AB = AY/AC = DF/AC. Thus, AY=DF

Now, by the SAS congruency criterion, AXYDEFAXYDEF

While we already have, AXY ~ ABC. This means DEF and ABC are similar. Hence Proved.

What Is Sas And Asa Congruence Rule

The SAS congruence rule states that if two sides of a triangle along with an angle in between is equal to two sides and included the angle of another triangle, then the two triangles are said to be congruent. Whereas the ASA congruence rule states that when two angles with an included side are equal to the two angles along with the included side of another triangle, then these two triangles are said to be congruent.

Also Check: Who You Spend Time With Is Who You Become Psychology

What Does Sas Stand For

What does SAS mean? This page is about the various possible meanings of the acronym, abbreviation, shorthand or slang term: SAS.

Filter by:

What does SAS mean?

Special Air Service, SAS

a specialist regiment of the British army that is trained in commando techniques of warfare and used in clandestine operations

Popularity rank for the SAS initials by frequency of use:

Couldn’t find the full form or full meaning of SAS?

Maybe you were looking for one of these abbreviations:

Discuss these SAS abbreviations with the community:

Report Comment

We’re doing our best to make sure our content is useful, accurate and safe.If by any chance you spot an inappropriate comment while navigating through our website please use this form to let us know, and we’ll take care of it shortly.

Caution Don’t Use Aaa

AAA means we are given all three angles of a triangle, but no sides.

This is not enough information to decide if two triangles are congruent!

Because the triangles can have the same angles but be different sizes:

Without knowing at least one side, we can’t be sure if two triangles are congruent.

Don’t Miss: Does Angelina Jolie Have Biological Children