Distance Versus Directed Distance And Displacement
Both distance and displacement measure the movement of an object. Distance cannot be negative, and never decreases. Distance is a scalar quantity, or a magnitude, whereas displacement is a vector quantity with both magnitude and direction. It can be negative, zero, or positive. Directed distance does not measure movement it measures the separation of two points, and can be a positive, zero, or negative vector.
The distance covered by a vehicle , person, animal, or object along a curved path from a point A to a point B should be distinguished from the straight-line distance from A to B. For example, whatever the distance covered during a round trip from A to B and back to A, the displacement is zero as start and end points coincide. In general the straight-line distance does not equal distance travelled, except for journeys in a straight line.
How To Calculate Displacement
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 24 people, some anonymous, worked to edit and improve it over time.There are 7 references cited in this article, which can be found at the bottom of the page. This article has been viewed 367,127 times.Learn more…
Displacement in physics refers to on object’s change in position. When you calculate displacement, you measure how “out of place” on object is based on its initial location and its final location. The formula you use for calculating displacement will depend on variables that are provided to you in a given problem. Follow these steps to calculate displacement.
Distances Between Sets And Between A Point And A Set
Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a low earth orbit, the first tends to be quoted , otherwise, e.g. for the EarthâMoon distance, the latter.
There are two common definitions for the distance between two non-empty subsets of a given metric space:
- One version of distance between two non-empty sets is the infimum of the distances between any two of their respective points, which is the everyday meaning of the word, i.e.
- d . d.}
- This is a symmetric premetric. On a collection of sets of which some touch or overlap each other, it is not “separating”, because the distance between two different but touching or overlapping sets is zero. Also it is not hemimetric, i.e., the triangle inequality does not hold, except in special cases. Therefore only in special cases this distance makes a collection of sets a metric space.
- The Hausdorff distance is the larger of two values, one being the supremum, for a point ranging over one set, of the infimum, for a second point ranging over the other set, of the distance between the points, and the other value being likewise defined but with the roles of the two sets swapped. This distance makes the set of non-empty compact subsets of a metric space itself a metric space.
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers
Related Questions And Answers
Why Euclidean distance is used?
What is Manhattan distance in Python?
How do you calculate chebyshev distance?
How do you calculate Euclidean distance?
What is Hamming distance in machine learning?
Why Euclidean distance is a bad idea?
What is distance in math?
What is Manhattan distance in data mining?
Finding The Distance Between Two Points
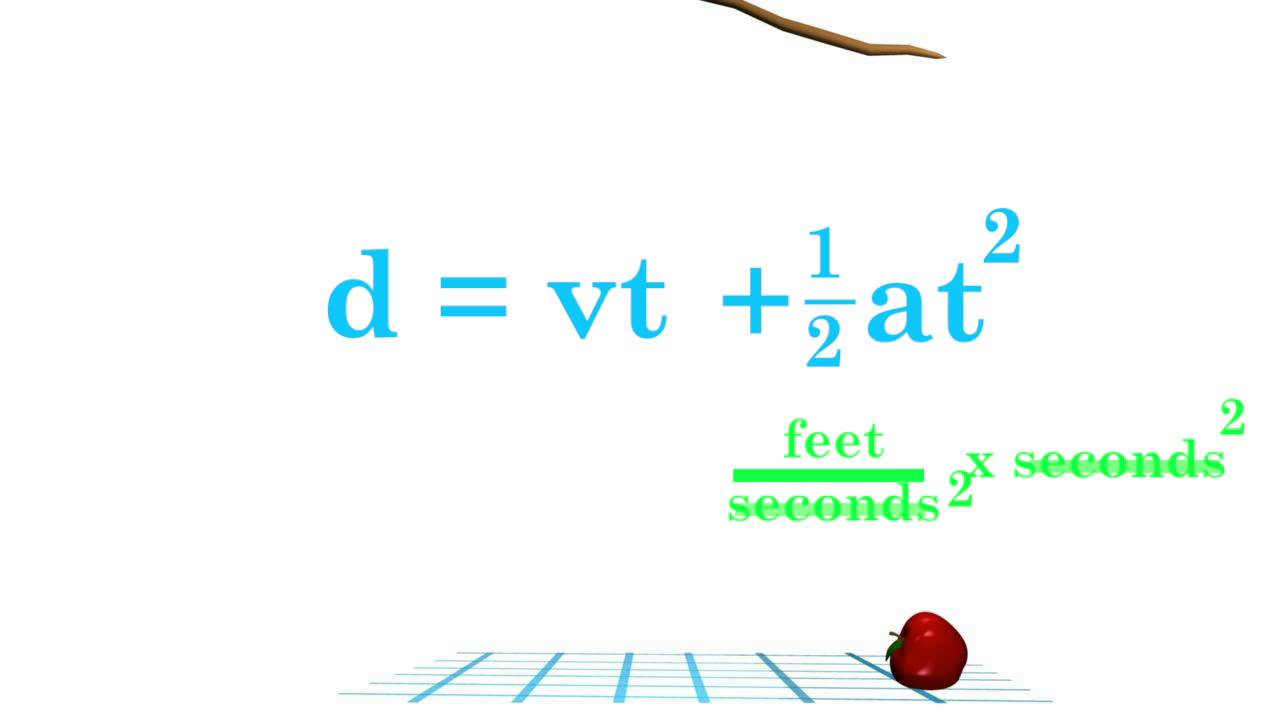
You May Like: Is Paris Jackson Michaels Biological Daughter
Using Force To Calculate Distance
- B
- #1
Jaxson said:Hey there, quick question. Can force be used to calculate distance/displacement. Like, if you know that for example, someone was hit in the chest with a certain amount of force, can that force be used to calculate a distance? Thanks.
- #3
- 21,318
- 5,156
- #5
Jaxson said:Sorry I’ll clarify. I might be completely wrong but because the units of momentum are kgm/s, it has time in it because the velocity has time in it, it could be used to calculate distance right?
change
How To Calculate Distance
Distance or displacement can be calculated using the above equation. If you are interested in the manual calculation of distance without using the mph calculator, check out the example below.
- Identify and write down the given values.
- Write down the distance formula
- Place the values and solve the equation.
Example 1: Find the distance
Find the distance covered by a car that is moving with an average speed of 60 m/s for 10 minutes?
Solution:
Step 1: Write down the given values.
t =10 minutes = 10 × 60 =600 seconds
va = 60 m/s
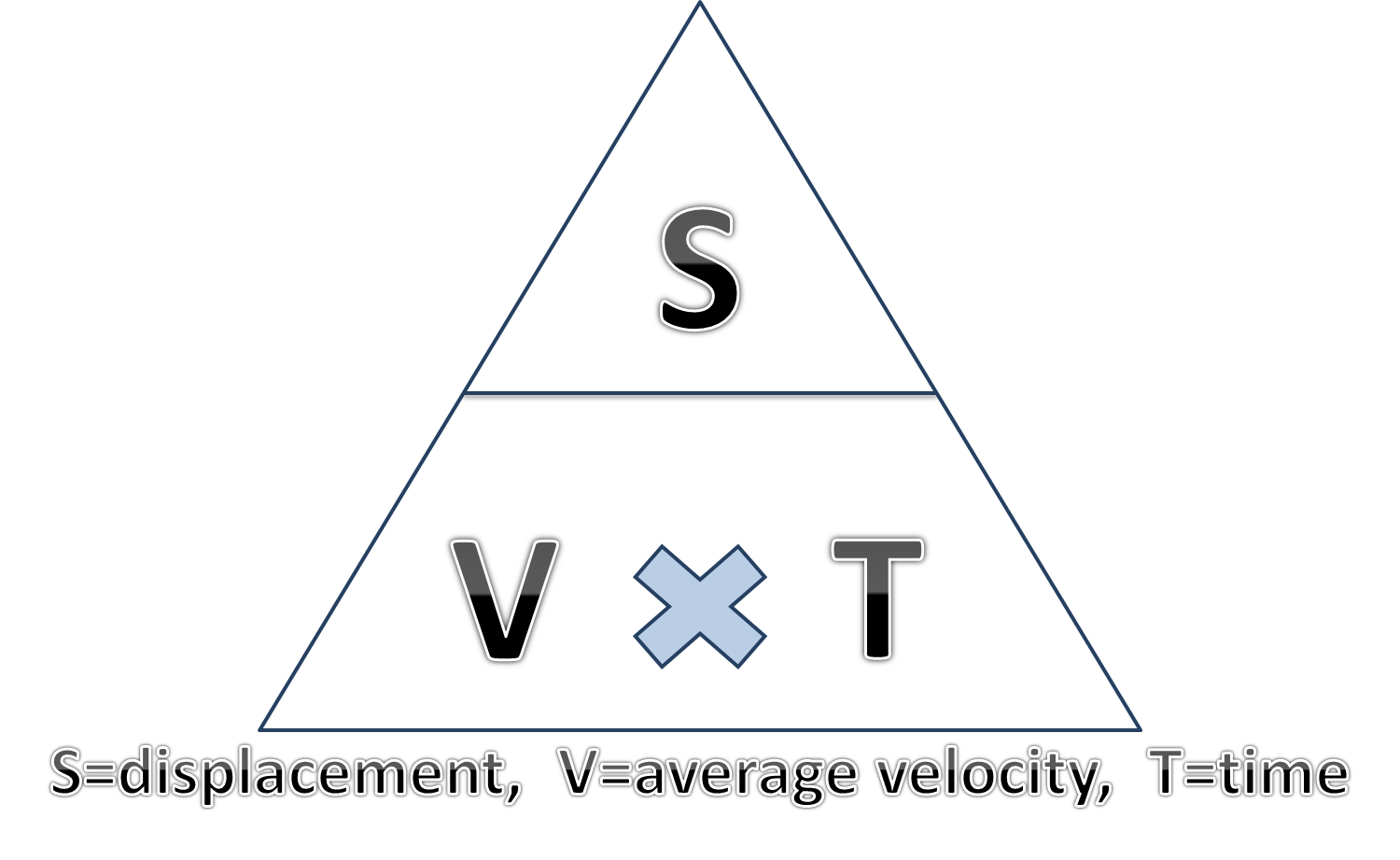
Step 2: Write down the equation of distance.
S = v × t
S = 60 × 600
S = 36000 m or 36 km
This tool can also be used as a travel time calculatorbecause you can find the total time using this tool.
Example 2: Find the average speed
Find the average speed of a car if it has covered the distance of 200 km in 3 hours?
Solution:
Step 1: Write down the values.
S = 200 km
Step 2: Use the distance equation to find the speed.
S = v × t
You May Like: What Is Elastic Force In Physics
How To Find Velocity
A car drives from Baltimore to Washington, D.C. in 1.5 hours. If you know that it’s 38 miles between the two cities, what was the car’s average velocity during the trip? Since, this is a trip that goes in one direction, the change in position is the same as distance. Since you know time and the distance, you can solve for velocity by plugging in the distance formula in physics:
So you know your answer is 25.3, but this isn’t quite complete: 25.3 what? Units are just as important as the numerical answer when it comes to physics problems, so don’t lose track of what you’re using to measure distance and time. Since you’re measuring distance in miles and time in hours, your final answer is miles divided by hours, or miles per hour.
Try another example:
A bicyclist completes a 550 meter race in 1.5 hours. What is the bike’s velocity in meters per second? Here, since you need to determine the velocity in meters per second, first convert time to seconds:
Then, plug your known variables into the velocity formula:
What Is A Distance
A distance-time graph shows how far an object has travelled in a given time. It is a simple line graph that denotes distance versus time findings on the graph.
Note: Curved lines on a distance-time graph indicate that the speed is changing.
You may also want to check out these topics given below!
Also Check: Holt Geometry Lesson 4.5 Practice B Answers
Distance And Displacement With Examples
Distance and Displacement
Distance is a scalar quantity representing the interval between two points. It is just the magnitude of the interval. However,Displacement is a vector quantity and can be defined by using distance concept. It can be defined as distance between the initial point and final point of an object. It must be the shortest interval connecting the initial and final points, that is a straight line.Let’s look at the below examples for deep understanding.
Look at the picture above, boy travels from D to A, A to B, B to C and C to D. Displacement from D to D is zero. However, distance traveled is not zero. It is equal to the perimeter of the rectangle.
Another example of distance and displacement is illustrated in Figure 1.2
John walks from the point A to B to C. What does the distance he travel? What is the displacement?
Let’s calculate first the distance that john travels. While calculating distance, we look at the numeric value of interval between traveled points. As you can see from Figure 1.2 he travels from A to B to C. Distance from A to B is 4m and B to C is 3 m. Their sum will give us total distance
4+3=7
Example: Look at the picture given below. An object moves from point A through B, C, D, E and stops at point F.
a) Find final displacement.
b) Find distance taken from point A to D.
Subsectiontwo Approaches: Area And Antidifferentiation
When the velocity of a moving object is positive, the object’s position is always increasing. We have established that whenever \ is constant on an interval, the exact distance traveled is the area under the velocity curve. When \ is not constant, we can estimate the total distance traveled by finding the areas of rectangles that approximate the area under the velocity curve.
Thus, we see that finding the area between a curve and the horizontal axis is an important exercise: besides being an interesting geometric question, if the curve gives the velocity of a moving object, the area under the curve tells us the exact distance traveled on an interval. We can estimate this area if we have a graph or a table of values for the velocity function.
In Example4.8, we encountered an alternate approach to finding the distance traveled. If \\) is a formula for the instantaneous velocity of a moving object, then \ must be the derivative of the object’s position function, \ If we can find a formula for \\) from the formula for \\text\) we will know the position of the object at time \ and the change in position over a particular time interval tells us the distance traveled on that interval.
For a simple example, consider the situation from Example4.1, where a person is walking along a straight line with velocity function \ = 3\) mph.
On the left-hand graph of the velocity function in Figure4.11, we see the relationship between area and distance traveled,
Definition4.12
Example4.13
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers
Stopping And Braking Distance
Imagine that you are driving your car on a regular street. Suddenly, you notice a child that runs across the street ahead of you. What happens during the next few stressful seconds?
First of all, some time will pass after the event began to happen, but before you react to it. This period is called the perception time. During this time, the car continues to move with the same speed as before, approaching the child on the road.
You might think that you hit the brake immediately, but there is always a small delay between the moment you notice the danger ahead and the instant in which you actually start to decelerate. This delay is called the reaction time. The car is still moving with the same speed.
After you start braking, the car will move slower and slower towards the child until it comes to a stop. The distance traveled from the moment you first hit the brake is called the braking distance. The stopping distance, on the other hand, is the total distance traveled during the perception and reaction time summed with the braking distance.
When Initial Velocity Acceleration And Time Values Are Specified
Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers
What Are Keplers 3 Laws In Simple Terms
There are actually three, Keplers laws that is, of planetary motion: 1) every planets orbit is an ellipse with the Sun at a focus 2) a line joining the Sun and a planet sweeps out equal areas in equal times and 3) the square of a planets orbital period is proportional to the cube of the semi-major axis of its
How Many Equations Are There To Calculate Distance
I am an app developer and I am trying to build a physics app to calculate distance based on the quantities the user gives. for example if the user gives initial speed, time and acceleration, using Newton’s 2nd equation, my program can calculate distance. So for example if I have six basic formulas which are:-
$$s = \frac$$$$d = ut + \frac$$$$v^2 – u^2 = 2ad$$$$s = \frac$$$$a = \frac$$$$v = u + at$$
$u$ and $v$ are initial and final speed
$t$ = time
$a$ = acceleration
Out of these, are there a definite number of equations I can derive to calculate distance if some combinations of quantities are given or will it be way too many as I might have some more equations.
Distance is calculated from one of the following direct integrals
Speed is known as a function of time
$$x = \int v\, t $$
Acceleration is known as a function of time
$$ x = \iint a\,t\,t $$
Speed is known as a function of distance
$$ t = \int \frac\,x \ \Rightarrow \mbox $$
Acceleration is known as a function of speed
$$ x = \int \frac\,v $$
For example, I am going to use both $a=a=g$ in and to demonstrate how you arrive at a particular equation for the given inputs:
$$ x = \iint g\,t\,t = \int g t \, t = v_0 t + \frac g t^2 $$$$ x = \int \frac \,v = \frac \left $$
Here are some other examples:
I’m going to assume you only want to find the distance whenever the acceleration is a constant value. If not, the suvat-equations
(U: initial velocity
A: acceleration
T: time) no longer apply.
$d_t$
$= u + a/2$
$= u + a/2$
You May Like: What Is The Molecular Geometry Of Ccl4
Calculate Distance From Acceleration And Velocity
Since we are considering motion of body or object with constant acceleration we have an equation of motion which relate all these quantities. This equation is the third equation of motion and is given by the relation
$v^2=u^2+2as$
Here,
$s$ is the distance traveled by the object in time $t$
$u$ is the initial velocity
$v$ is the final velocity and
$a$ is the constant acceleration of the moving object
You can use this formula in various situations involving distance, initial velocity, final velocity and acceleration motion. You need to have a knowledge of three quantities to find the fourth quantity. It must be noted that this equation does not involve the time interval of motion of the object.
Time Intervals And Distances
Differences and values
Wrong Track: Speed is just distancetime, and that’s all there is to it.
Right Lines: Distance is the difference between two locations along your track. To find your speed you also need a time interval, the difference between two times on the clock . So speed is calculated from difference in location along the track
and difference in time
.
Speed is always from someone’s point of view
Thinking about the learning
Where am I now?
is a question that requires a position for an answer .
What time is it now?
is a question that requires a time for an answer .
Repeat these questions after a journey and you’ll get another position and a different time.
To find a speed you need to combine the two positions, and maybe some more information to find the distance covered on your journey, as well as combine the two clock readings to find the duration of your journey.
Thinking about the teaching
Trying to cut corners to make things simpler often stores up difficulties for the future. This is a place to take care. We’d suggest that you avoid using just time
, unless you mean time of day. Avoid What’s the time for that journey?
, replacing it with something more natural:
Teacher: How long did the journey take?
This kind of phrasing implies a duration, an interval of time. Distance is less of an issue, as we’re less likely to use the word to mean many things, as we do for time .
distance = positionend positionbegin
duration = timeend timebegin
speed = distancetime
Read Also: What Does Abiotic Mean In Biology