Solved Example On Distance Formula
Example 1
Suppose a dog runs from one end of the street to another end of the street and the street is 80.0 meters across. Moreover, the takes 16.0 seconds to cross reach the end of the street. Now, calculate the speed of the dog?
Solution:
As we discussed earlier the distance formula can be interchanged to find the speed of the body or object.So, the distance and time is present in the question that is 80.0 m and 16.0 s respectively. Now, put these values in the question
Speed = \
S = \
S = 5.0 m/s
So, the speed of the dog will be 5 m/s.
Example 2
Now, in another situation, a golf cart driver is driving the golf cart that has a maximum speed of 27.0 km/h. Furthermore, the driver drives the car for 10.0 minutes. So, calculate the distance covered by the golf cart with its top speed in 10.0 minutes?
Solution:
For solving this problem first of all we need to convert the speed from km/h to m/s and time from minutes to seconds.Calculating speed
s = 27.0 km/h
s = 27.0 ×\ × \ × \ × \
So, s = 7.50 m/s
Displacement Definition And Explanation
On the other hand, displacement is demonstrated as a vector quantity, which implies that the displacement of any body is dependent on both magnitude and direction of motion of that body. The displacement of a body is described as the total motion of the body or we can also define it as the minimum distance between the initial starting point of the body and the end-point of the body. For instance, take the same example as mentioned in the previous paragraph. From that, the overall displacement of that specific body is nothing but the length of the line which helps join both the positions. Displacement of the body is either shorter or equal to that of the distance traveled by that body but can never be greater. In contrast to the distance, displacement will not provide a proper idea or information about the path of the object in which it is being traveled.
Distance Definition And Explanation
Distance is a scalar quantity, and it means that the distance of any body will never depend on the direction of its motion. Distance only includes the magnitude. Distance can be described as the total path traveled by any particular body or object. For instance, in case a bike travels north for 10 km and then takes a turn to travel in the east direction for another 5 km, the bike covers a distance of 15 km in total and it shows that it does not matter in which direction the journey happened. Distance can never be termed as negative or zero. Meanwhile, it is always more than that of the displacement of the body. When you consider the distance covered by any particular body, it will give an overall idea of how it is being covered, i.e. in which path.
Don’t Miss: How To Do Elimination In Math
Distances Between Sets And Between A Point And A Set
Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a low earth orbit, the first tends to be quoted , otherwise, e.g. for the EarthâMoon distance, the latter.
There are two common definitions for the distance between two non-empty subsets of a given metric space:
- One version of distance between two non-empty sets is the infimum of the distances between any two of their respective points, which is the everyday meaning of the word, i.e.
- d . d.}
- This is a symmetric premetric. On a collection of sets of which some touch or overlap each other, it is not “separating”, because the distance between two different but touching or overlapping sets is zero. Also it is not hemimetric, i.e., the triangle inequality does not hold, except in special cases. Therefore only in special cases this distance makes a collection of sets a metric space.
- The Hausdorff distance is the larger of two values, one being the supremum, for a point ranging over one set, of the infimum, for a second point ranging over the other set, of the distance between the points, and the other value being likewise defined but with the roles of the two sets swapped. This distance makes the set of non-empty compact subsets of a metric space itself a metric space.
Distance Versus Directed Distance And Displacement
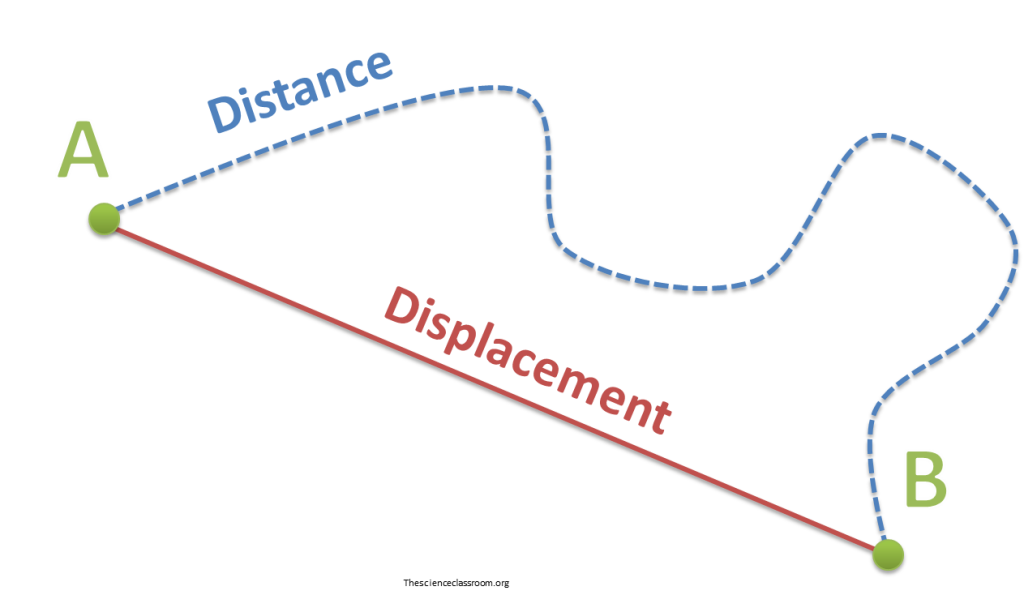
Both distance and displacement measure the movement of an object. Distance cannot be negative, and never decreases. Distance is a scalar quantity, or a magnitude, whereas displacement is a vector quantity with both magnitude and direction. It can be negative, zero, or positive. Directed distance does not measure movement; it measures the separation of two points, and can be a positive, zero, or negative vector.
The distance covered by a vehicle , person, animal, or object along a curved path from a point A to a point B should be distinguished from the straight-line distance from A to B. For example, whatever the distance covered during a round trip from A to B and back to A, the displacement is zero as start and end points coincide. In general the straight-line distance does not equal distance travelled, except for journeys in a straight line.
Also Check: What Is Frictional Force In Physics
Related Questions And Answers
Why Euclidean distance is used?
What is Manhattan distance in Python?
How do you calculate chebyshev distance?
How do you calculate Euclidean distance?
What is Hamming distance in machine learning?
Why Euclidean distance is a bad idea?
What is distance in math?
What is Manhattan distance in data mining?
The Importance Of Reference Frames
This takes on greater importance in advanced physics, but it’s important to emphasize that when physicists declare that something is “in motion,” they mean with respect to a coordinate system or other reference frame that is fixed with respect to the variables in the problem. For example, it’s fair to say that if a road’s speed limit is 100 km/hr, it is implies that the Earth itself, though clearly not stationary in absolute terms, is treated as such in context.
Albert Einstein is best known for his theory of relativity, and his special relativity idea was one of the most groundbreaking in the history of modern thought. Without incorporating reference frames into his work, Einstein would not have been able to adapt Newton’s equations in the early 20th century to suit relativistic particles, which deal with very high speeds and low masses.
Related Articles
Also Check: Why Are There Different Branches Of Chemistry
Examples Of Distance And Displacement
Question 1. John travels 250 miles to North but then back-tracks to South for 105 miles to pick up a friend. What is Johns total displacement?
Answer: Johns starting position; Xi= 0.
Her final position Xf is the distance travelled N minus the distance South.
Calculating displacement, i.e.D.
D = 0
D = 145 mi N
Question 2.;An object moves along the grid through points A, B, C, D, E, and F as shown below. The side of square tiles measures 0.5 km.
a) Calculate the distance covered by the moving object.
b) Find the magnitude of the displacement of the object.
Solution:
Read More:Difference Between Distance and Displacement
Watch and learn the laws of motion with the help of animations.
We, at BYJUS, strongly believe that a spirit of learning and understanding can only be inculcated when students are curious and that curiosity can be brought about by creative and effective teaching. It is this approach that makes our lectures so successful and gives our students an edge over their counterparts.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Misconception Alert: Distance Traveled Vs Magnitude Of Displacement
It is important to note that the distance traveled, however, can be greater than the magnitude of the displacement . For example, the professor could pace back and forth many times, perhaps walking a distance of 150 m during a lecture, yet still end up only 2.0 m to the right of her starting point. In this case her displacement would be +2.0 m, the magnitude of her displacement would be 2.0 m, but the distance she traveled would be 150 m. In kinematics we nearly always deal with displacement and magnitude of displacement, and almost never with distance traveled. One way to think about this is to assume you marked the start of the motion and the end of the motion. The displacement is simply the difference in the position of the two marks and is independent of the path taken in traveling between the two marks. The distance traveled, however, is the total length of the path taken between the two marks.
Don’t Miss: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Position Time And Other Variables Of Motion
Specifying an object’s position in space is a starting point for countless physics problems. For the most part, beginning and intermediate exercises use one-dimensional or two-dimensional systems to keep the problems from being overly difficult, but the principles extend to three-dimensional space as well.
A particle moving in two-dimensional space can be assigned x- and y-coordinates for its position, its rate of change of position and its rate of change of velocity . Time, of course, is labeled t.
S Of Creating Entanglement
Entanglement is usually created by direct interactions between subatomic particles. These interactions can take numerous forms. One of the most commonly used methods is spontaneous parametric down-conversion to generate a pair of photons entangled in polarisation. Other methods include the use of a fiber coupler to confine and mix photons, photons emitted from decay cascade of the bi-exciton in a quantum dot, the use of the HongOuMandel effect, etc. In the earliest tests of Bell’s theorem, the entangled particles were generated using atomic cascades.
It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping. Two independently prepared, identical particles may also be entangled if their wave functions merely spatially overlap, at least partially.
Also Check: Geometry Wars 2 Smile Achievement
What Is A Distance
A distance-time graph shows how far an object has travelled in a given time.; It is a simple line graph that denotes distance versus time findings on the graph.
Note:;Curved lines on a distance-time graph indicate that the speed is changing.
You may also want to check out these topics given below!
How To Calculate Distance
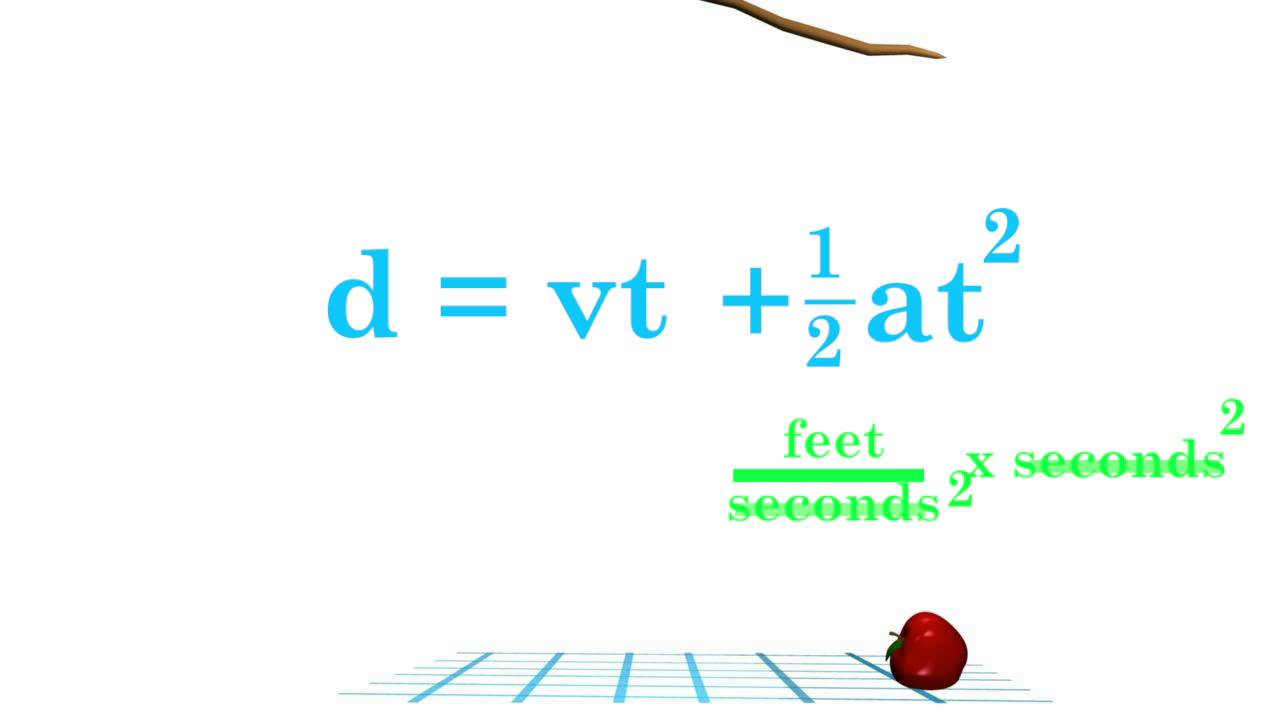
Distance or displacement can be calculated using the above equation. If you are interested in the manual calculation of distance without using the mph calculator, check out the example below.
- Identify and write down the given values.
- Write down the distance formula
- Place the values and solve the equation.
Example 1: Find the distance
Find the distance covered by a car that is moving with an average speed of 60 m/s for 10 minutes?
Solution:
Step 1: Write down the given values.
t =10 minutes = 10 × 60 =600 seconds
va = 60 m/s
Step 2: Write down the equation of distance.
S = v × t
S = 60 × 600
S = 36000 m or 36 km
This tool can also be used as a travel time calculatorbecause you can find the total time using this tool.
Example 2: Find the average speed
Find the average speed of a car if it has covered the distance of 200 km in 3 hours?
Solution:
Step 1: Write down the values.
S = 200 km
Step 2: Use the distance equation to find the speed.
S = v × t
Recommended Reading: How Did Geography And Religion Influence Ethiopia’s Development
Distance And Displacement With Examples
Distance and Displacement
Distance is a scalar quantity representing the interval between two points. It is just the magnitude of the interval. However,Displacement is a vector quantity and can be defined by using distance concept. It can be defined as distance between the initial point and final point of an object. It must be the shortest interval connecting the initial and final points, that is a straight line.Let’s look at the below examples for deep understanding.
Look at the picture above, boy travels from D to A, A to B, B to C and C to D. Displacement from D to D is zero. However, distance traveled is not zero. It is equal to the perimeter of the rectangle.
Another example of distance and displacement is illustrated in Figure 1.2
John walks from the point A to B to C. What;does the distance he travel? What is the displacement?
Let’s calculate first the distance that john travels. While calculating distance, we look at the numeric value of interval between traveled points. As you can see from Figure 1.2 he travels from A to B to C. Distance from A to B is 4m and B to C is 3 m. Their sum will give us total distance;
4+3=7
Example:;Look at the picture given below. An object moves from point A through B, C, D, E and stops at point F.
a) Find; final displacement.
b) Find distance taken from point A to D.
Entanglement As A Resource
In quantum information theory, entangled states are considered a ‘resource’, i.e., something costly to produce and that allows to implement valuable transformations. The setting in which this perspective is most evident is that of “distant labs”, i.e., two quantum systems labeled “A” and “B” on each of which arbitrary quantum operations can be performed, but which do not interact with each other quantum mechanically. The only interaction allowed is the exchange of classical information, which combined with the most general local quantum operations gives rise to the class of operations called LOCC . These operations do not allow the production of entangled states between the systems A and B. But if A and B are provided with a supply of entangled states, then these, together with LOCC operations can enable a larger class of transformations. For example, an interaction between a qubit of A and a qubit of B can be realized by first teleporting A’s qubit to B, then letting it interact with B’s qubit and then teleporting the qubit back to A. Two maximally entangled states of two qubits are used up in this process. Thus entangled states are a resource that enables the realization of quantum interactions in a setting where only LOCC are available, but they are consumed in the process. There are other applications where entanglement can be seen as a resource, e.g., private communication or distinguishing quantum states.
Also Check: Holt Mcdougal Pre Algebra Workbook
Distance In Euclidean Space
In the Euclidean spaceRn, the distance between two points is usually given by the Euclidean distance . Other distances, based on other norms, are sometimes used instead.
For a point and a point , the Minkowski distance of order p is defined as:
| 1-norm distance |
| ) . -y_|,|x_-y_|,\ldots ,|x_-y_|\right).} |
p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality does not hold.
The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler: the “intuitive” idea of distance.
The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance, because it is the distance a car would drive in a city laid out in square blocks .
The infinity norm distance is also called Chebyshev distance. In 2D, it is the minimum number of moves kings require to travel between two squares on a chessboard.
The p-norm is rarely used for values of p other than 1, 2, and infinity, but see super ellipse.
In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body does not change with rotation.
Violations Of Bell’s Inequality
Local hidden variable theories fail, however, when measurements of the spin of entangled particles along different axes are considered. If a large number of pairs of such measurements are made , then statistically, if the local realist or hidden variables view were correct, the results would always satisfy Bell’s inequality. A number of experiments have shown in practice that Bell’s inequality is not satisfied. However, prior to 2015, all of these had loophole problems that were considered the most important by the community of physicists. When measurements of the entangled particles are made in moving relativistic reference frames, in which each measurement occurs before the other, the measurement results remain correlated.
The fundamental issue about measuring spin along different axes is that these measurements cannot have definite values at the same timethey are incompatible in the sense that these measurements’ maximum simultaneous precision is constrained by the uncertainty principle. This is contrary to what is found in classical physics, where any number of properties can be measured simultaneously with arbitrary accuracy. It has been proven mathematically that compatible measurements cannot show Bell-inequality-violating correlations, and thus entanglement is a fundamentally non-classical phenomenon.
You May Like: What Does Coordinate Mean In Math
Difference Between Distance And Displacement
The basic difference between Distance and displacement is that distance is the length of a path between two points and displacement is the shortest distance between two points.
More differences between distance Vs displacement are tabulated below.
You may also be interested in the: Difference between speed and velocity