Solved Questions Based On Acceleration Formula With Mass And Force
Question 1 A car of mass 1000 Kg is moving with velocity 10 m/s and is acted upon by a forward force of 1000 N due to engine and a retarding force of 500N due to friction. What will be its velocity after 10 seconds?
Solution Here it is given that\\\We have to find velocity \ after 10 seconds.Net forward force,\\Acceleration\From kinematic equation of uniformly accelerated motion\So we have \
Question 2 A force of 72 dynes is inclined to the horizontal at an angle of \. Find the acceleration in the mass of \, which moves in a horizontal direction.
Solution Here it is given in the question that\, \, \The horizontal component of the force is \\Acceleration,\
Further Reading
Tangential And Centripetal Acceleration
The velocity of a particle moving on a curved path as a function of time can be written as:
- v
- , \mathbf & = }}\\& =}\mathbf _ }+v _ }}}\\& =}\mathbf _ }+}}\mathbf _ }\ ,\end}}
where un is the unit normal vector to the particle’s trajectory , and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the normal or radial acceleration .
Geometrical analysis of three-dimensional space curves, which explains tangent, normal and binormal, is described by the FrenetSerret formulas.
- } is the uniform rate of acceleration.
In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e. g., the trajectory of a projectile in a vacuum near the surface of Earth.
rva
- For a given speed , the magnitude of this geometrically caused acceleration is inversely proportional to the radius r
. } =-\omega ^\mathbf \ .}
- . =r\alpha .}
The sign of the tangential component of the acceleration is determined by the sign of the angular acceleration , and the tangent is always directed at right angles to the radius vector.
Calculating Acceleration From A Force
Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers
Summary Of Kinematic Equations
Before we get into the examples, letâs look at some of the equations more closely to see the behavior of acceleration at extreme values. Rearranging Equation 3.12, we have
From this we see that, for a finite time, if the difference between the initial and final velocities is small, the acceleration is small, approaching zero in the limit that the initial and final velocities are equal. On the contrary, in the limit t for a finite difference between the initial and final velocities, acceleration becomes infinite.
Similarly, rearranging Equation 3.14, we can express acceleration in terms of velocities and displacement:
Thus, for a finite difference between the initial and final velocities acceleration becomes infinite in the limit the displacement approaches zero. Acceleration approaches zero in the limit the difference in initial and final velocities approaches zero for a finite displacement.
Acceleration Formula Important Facts
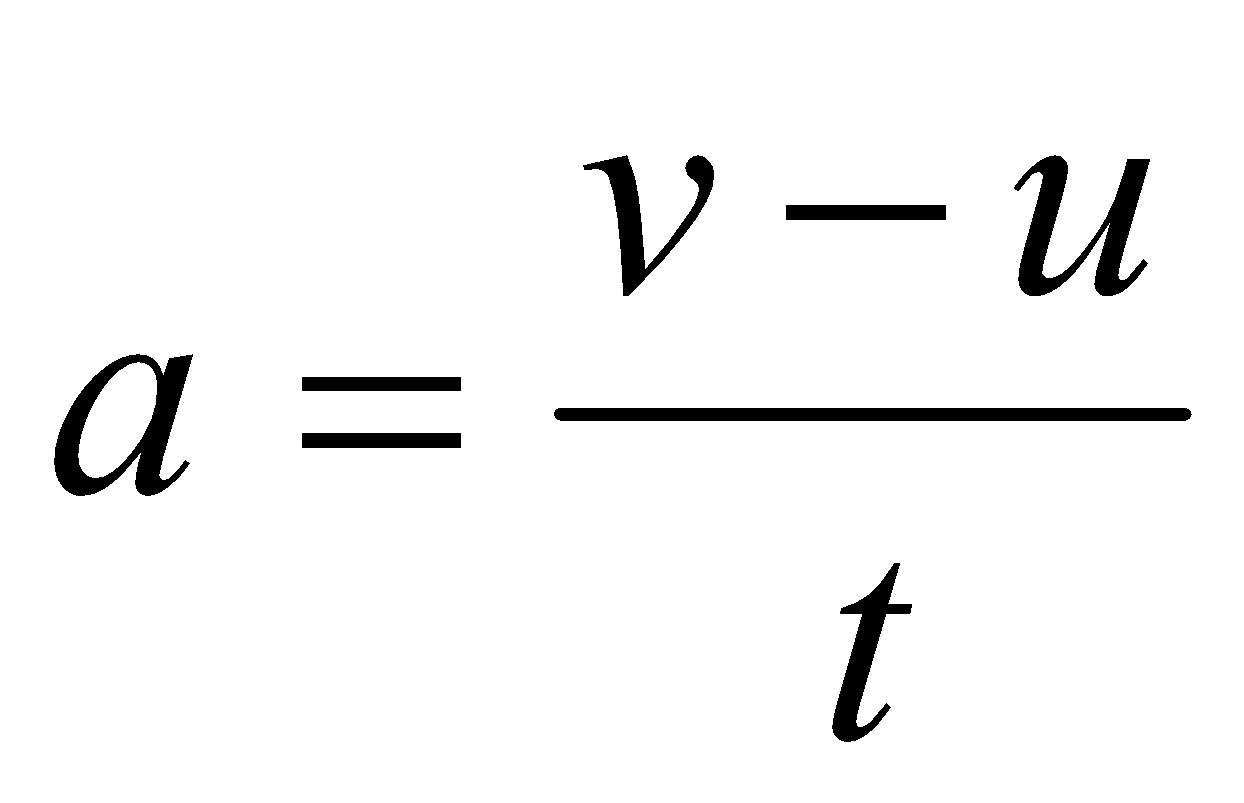
You May Like: Why Are There Different Branches Of Chemistry
How To Calculate Acceleration: Step
Now well breakdown the acceleration formula step-by-step using a real example.
A race car accelerates from 15 m/s to 35 m/s in 3 seconds. What is its average acceleration?
First, write the acceleration equation.
$$a = /$$
Next, define your variables.
$a$ = what we are solving for
$$V = 35 m/s$$
Now, plug your variables into the equation and solve:
$$A =/s}/$$
$$A = / m/s^2$$
$$A = -23.2/1.4 m/s^2$$
$$A = -16.57 m/$$
How To Find The Acceleration From The Velocity Difference
First things first – both acceleration and velocity are vectors. From the previous section, we know that the acceleration results from subtracting the final and the initial velocity divided by the time difference.
Imagine a sphere in the Cartesian coordinates system. The initial velocity is v0 = m/s, and the final velocity equals v1 = m/s. The velocity changed in time interval t = 5 s. We can ask two questions: What is the acceleration? and How to calculate the magnitude of acceleration? Let’s find out:
-
Evaluate the velocities’difference. For vectors, subtract each of the coordinates separately:
v1 – v0 = – = = = m/s
-
Divide both components by time difference: =
-
The result is our acceleration: a = m/s².
So how to find the magnitude of the acceleration? Let’s use the formula with acceleration coordinates:
-
Square each of the components: ² = 1.44, ² = 0.16
-
Add these numbers: 1.44 + 0.16 = 1.6
-
Estimate the square root of this value: = 1.265. We will stick with four significant figures and
-
That’s all! The magnitude of the acceleration is 1.265 m/s².
You May Like: Intermediate Algebra Final Exam Answers
How Do You Find Angular Acceleration
Acceleration Formula In Physics
In Physics, Acceleration is described as the rate of change of velocity of an object, irrespective of whether it speeds up or slows down. If it speeds up, acceleration is taken as positive and if it slows down, the acceleration is negative. It is caused by the net unbalanced force acting on the object, as per Newtons Second Law. Acceleration is a vector quantity as it describes the time rate of change of velocity, which is a vector quantity. Acceleration is denoted by a. Its SI unit is m/s2 and dimensions are M0L1T2.
If v0, vt and t represents the initial velocity, final velocity and the time taken for the change in velocity, then, the acceleration is given by:
In one dimensional motion, we can use \
Acceleration Formula
If \represents displacement vector and \represents the velocity, then
Acceleration: \
In one dimensional motion, where x is the displacement, and \is the velocity, then
Example 1:
A car starts from rest and achieves a speed of 54 km/h in 3 seconds. Find its acceleration?
Solution:
Also Check: Michael Jackson’s Biological Kids
Displacement And Position From Velocity
To get our first two equations, we start with the definition of average velocity:
Substituting the simplified notation for Î
Solving for x gives us
where the average velocity is
reflects the fact that when acceleration is constant, v v â is just the simple average of the initial and final velocities. Figure 3.18 illustrates this concept graphically. In part of the figure, acceleration is constant, with velocity increasing at a constant rate. The average velocity during the 1-h interval from 40 km/h to 80 km/h is 60 km/h:
In part , acceleration is not constant. During the 1-h interval, velocity is closer to 80 km/h than 40 km/h. Thus, the average velocity is greater than in part .
Solved Examples On Acccerelation Formula
Question- A woman is traveling by her sports car at a constant velocity v = 5.00 m/s. When she steps on the gas, it makes the car to accelerate forward. Further, past 10.0 seconds, she stops the acceleration and continues a constant velocity v = 25.0 m/s. Calculate the acceleration of the car.
Answer- In the forward direction, initial velocity is \ = 5.00 m/s. Further, the final velocity in the forward direction is \ = 25.0 m/s. The time in which the change took place is 10.0 s. Therefore, the acceleration is in the forward direction, with a value:
a = \
a = \
a = \
a = 2.00 m/s2
Therefore, we see that the acceleration of the car is 2.00 m/s2 forward.
Question- A man takes a rock and drops it off from a cliff. It falls for 15.0 s before it hits the ground. The acceleration due to gravity g = 9.80 m/s2. Calculate the velocity of the rock the moment before it had hit the ground.
Answer- The man released the rock from rest, therefore, we get the initial velocity as \ = 0.00 m/s. The time for the change to take place is 15.0 s. The acceleration for this is 9.80 m/s2. Therefore, to find the velocity we will rearrange the equation like:
a = \ + at
\ + at
\ = 0.00 m/s +
\ = 147 m/s
Therefore, as the rock is falling, the direction of the velocity is down.
Also Check: Span Of Vectors
What Is Tangential Acceleration
Tangential acceleration is defined as the rate of change of the tangential velocity of a particle in a circular orbit. There are 3 possible values for tangential acceleration. First is when the magnitude of the velocity vector increases with time, tangential acceleration is greater than zero. Second is when the magnitude of the velocity vector decreases with time, tangential acceleration is less than zero. The third possibility is when the magnitude of the velocity vector remains constant, the tangential acceleration is equal to zero.
How To Derive The Equation Of Centripetal Acceleration

figure 1: derivation of the equation of Centripetal acceleration
In the above figure , a particle is moving in a circle with a steady speed v. The diagram shows how the velocity vector changes direction as the particle moves from P to P in time t.
In figure 2, the velocity vectors from the previous diagram have been used in a triangle of vectors.
In figure 2, Velocity at P and P is shown as v which is actually the uniform speed v at these 2 points. At P and P velocity is different because of different directions at these 2 points.
The v vector represents the change in velocity because it is the velocity vector that must be added to the velocity at P to produce the new velocity at P. Here, we will use the concepts of the triangle law of vector addition.
Note that the change in velocity is towards O. In other words, the particle has an acceleration towards the centre of the circle. This is called centripetal acceleration.
If a is the centripetal acceleration, a = v/t..
But, from the triangle above, = v/v
So, v = v
From and we get: a = v/t = v /t = v Using v =r, and = v/r we get 2 equations of a from equation :
a = v = v. v/r = v2 r .
a = v = r. = 2 r .
For example, if a particle is moving at a steady speed of 5 m s-1 in a circle of radius 5 m, its centripetal acceleration ais found using the middle equation: a= 52/5 = 5 m s-2 .
Also Check: What Is Surface Area In Math
Unit Relationships For M=f/a
Solves for mass: Problem 3
Here we will show that in the equation F=mathe acceleration vector, a, has the same direction as thenet force vector, F.
First, recall that when we multiply a scalar times a vector, the resultis a vector that has the same direction as the original. So if we multiplyscalar 2 times vector P we get a vector as the result whichhas the same direction as vector P. We could give thisresult vector a name, say Q. This is all shown in thefollowing animation:
Now let’s see how all this works out with the F and thea vector in the equation F=ma.Note that the right side of the equation is mass times acceleration. Mass isa scalar, and acceleration is a vector. So the right side of this equationis a scalar times a vector. This multiplication yields a vector that iscalled the force vector, or F, which is on the left side ofthe equation.
As above with P and Q, vector ais in the same direction as vector F. Therefore, theacceleration of an object is in the same direction of the applied net force.Here is another animation showing all of this for the a andF vectors:
And so we have shown that the formula F=macontains the information that an object’s acceleration vector is aimed inthe same direction as its applied net force vector.
6 m/s2 =
6 m/s2 = 6 m/s2
There is really nothing special about our choice offactor changes here. Try changing the mass by a factor of 5 and calculate tosee the acceleration change by a factor of 1/5.
How To Calculate Acceleration: The 3 Formulas You Need
“Whoa, you really went from zero to sixty there!”
Have you ever heard someone use the idiom “zero to sixty” like I did in the above example? When someone says something went from “zero to sixty,” theyre really saying that things accelerated very quickly. Acceleration is the amount by which the velocity of something changes over a set period of time.
In this article, well be talking all about acceleration: what it is and how to calculate it. Buckle up!
Recommended Reading: Geometry Angle Addition Worksheet
Magnitude Of Acceleration Calculator
Welcome to our magnitude of acceleration calculator – a fantastic tool that knows how to find the magnitude ofacceleration. But that’s not the end of the story. Read the article to learn:
- What does acceleration mean?
- Is there a single magnitude of acceleration formula?
- How to find the acceleration from the velocity difference?
If you’ve asked yourself one of these questions recently , this is the best place to find the answer!
How Is Acceleration Different From Velocity
Velocity is the rate of change of position with respect to time, whereas acceleration is the rate of change of velocity. Both are vector quantities , but the units of velocity are meters per second while the units of acceleration are meters per second squared.
You May Like: How Do You Find Ksp
How To Find The Magnitude Of Acceleration
There are a few ways to estimate the magnitude of acceleration. We implement three of them in this magnitude of acceleration calculator:
According to Newton’s second law, the acceleration a is proportional tothe net forceF and inversely proportional to the object’smassm. So how to calculate the magnitude of acceleration? By analogy – the magnitude of the acceleration is proportional to the magnitude of this force. Let’s convert these words to the magnitude of acceleration formula:
|a| = |F| / m.
Here, bolded symbols represent vectors, and vertical lines denote a vector’s magnitude, the absolute value, which is always positive .
As acceleration is a vector, we can always get this quantity by summing up the acceleration’s components. We can use a simple addition of vectors. In general, for two components, we can write:
a = a1 + a2.
In the Cartesian plane, we can use x- and y-coordinates , and if we are working with a circular motion, it’s worth implementing tangential and centripetal components .
In either case, you receive a vector. And how to find the magnitude of acceleration? As both components are perpendicular to each other, square the values and work out the square root of the sum:
|a| = .
In three-dimensional space the magnitude of acceleration formula extends to:
|a| = .
Acceleration Formula With Velocity And Time
Contents
In this article, we will look at the acceleration formula with velocity and time. Before going any further let us define what is acceleration.Acceleration is change in velocity over timeThere are two ways to find the acceleration
- Acceleration formula with velocity and time
- acceleration formula with mass and force
In this article, we will look at the formula for acceleration with velocity and time. We use the acceleration formula with velocity and time when we do not have any knowledge of force acting on the body. We only have information about
- Change in velocity
- Time
Read Also: Paris Jackson Biological
What Is Angular Acceleration In Physics
Angular acceleration, also called rotationalacceleration, is a quantitative expression of the change inangular velocity that a spinning object undergoes per unittime. It is a vector quantity, consisting of a magnitude componentand either of two defined directions or senses.
Subsequently, one may also ask, what is formula of angular acceleration?
It is the change in the angular velocity, dividedby the change in time. The average angular acceleration isthe change in the angular velocity, divided by the change intime. The magnitude of the angular acceleration is given bythe formula below. The unit of angular accelerationis radians/s2.
Furthermore, what does constant angular acceleration mean? Any time the speed of an object is changing, it has anacceleration. Angular acceleration is defined as therate at which the angular velocity is changing. If theFerris wheel speeds up at a constant rate, then we would saythat the angular acceleration isconstant.
Correspondingly, what is angular velocity and acceleration?
Acceleration is the change in velocity ofmoving an object with respect to time. If the object moves on acircular direction than its velocity is called angularvelocity. The angular acceleration is also known asrotational acceleration. It is a quantitative expression ofthe change in angular velocity per unit time.
What is the unit of angular velocity?
You May Like Also