What Is Initial Value In Math

New York State Common Core Math Grade 8 Module 6 Lesson 2

Lesson 2 Summary

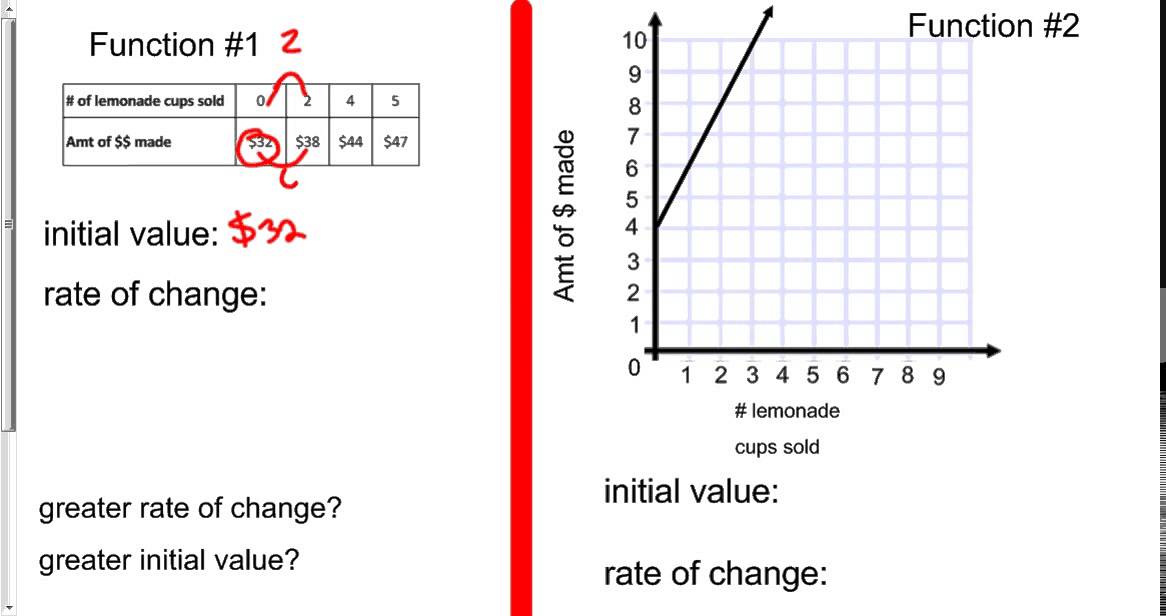
When a linear function is given by the equation of a line of the form y = mx +c, the rate of change is m and initial value is b. Both are easy to identify.

The rate of change of a linear function is the slope of the line it represents. It is the change in the values of y per a one unit increase in the values of x.

• A positive rate of change indicates that a linear function is increasing.
• A negative rate of change indicates that a linear function is decreasing.
• Given two lines each with positive slope, the function represented by the steeper line has a greater rate of change.

The initial value of a linear function is the value of the y-variable when the x value is zero.

In 2008, a collector of sports memorabilia purchased 5 specific baseball cards as an investment. Let y represent the cards resale value and x represent the number of years since purchase. Each of the cards’ resale values after 0, 1, 2, 3, and 4 years could be modeled by linear equations as follows:

Card A: y = 5 – 0.7x

Card B: y = 4 + 2.6x

Card C: y = 10 + 0.9x

Card D: y = 10 – 1.1x

Card E: y = 8 + 0.25x

1. Which card are decreasing in value each year? How can you tell?

2. Which card had the greatest initial values at purchase ?

3. Which card is increasing in value the fastest from year to year? How can you tell?

4. If you were to graph the equations of the resale values of Card B and Card C, which card’s graph line would be steeper? Explain.

Existence And Uniqueness Of Solutions

The PicardâLindelöf theorem guarantees a unique solution on some interval containing t0 if f is continuous on a region containing t0 and y0 and satisfies the Lipschitz condition on the variable y.The proof of this theorem proceeds by reformulating the problem as an equivalent integral equation. The integral can be considered an operator which maps one function into another, such that the solution is a fixed point of the operator. The Banach fixed point theorem is then invoked to show that there exists a unique fixed point, which is the solution of the initial value problem.

An older proof of the PicardâLindelöf theorem constructs a sequence of functions which converge to the solution of the integral equation, and thus, the solution of the initial value problem. Such a construction is sometimes called “Picard’s method” or “the method of successive approximations”. This version is essentially a special case of the Banach fixed point theorem.

Hiroshi Okamura obtained a necessary and sufficient condition for the solution of an initial value problem to be unique. This condition has to do with the existence of a Lyapunov function for the system.

A simple example is to solve y

Introduction To Differential Equations

Part 2: Initial value problems

Our mathematical model describing the spread of the rumor consists of two parts. The first is the differential equation

dS/dt = k S S = 2

This second condition is called an initial condition — the value of dependent variable at the first value of the independent variable under consideration. A differential equation together with an initial condition is called an initial value problem. The implied “problem” is to find a function that satisfies both conditions.

We need to discuss the term “solution.” A solution to a differential equation is a function that satisfies the relation for all values of the independent variable under consideration. For example, Y = exp is a solution of the differential equation

dY/dt = Yt

The function Y = 3 exp is another solution to this differential equation.

A solution to an initial value problem is a solution to the differential equation that also satisfies the initial condition. So, Y = exp is a solution to the initial value problem

dY/dt = YtY = 1

but, Y = 3 exp is not.

One can find a symbolic description for the solution of the initial value problem

dS/dt = k S tS = 2

Here is such a description:

For now, we will not discuss how you could find such a solution. Rather, we will just verify that it works.

dS/dt = k S tS = 2

Recommended Reading: Who Are Paris Jackson’s Biological Parents

What Is An Initial Condition

An initial condition is a starting point; Specifically, it gives dependent variable values for a certain independent variable. It allows you to zoom in on a specific solution.

In general, an initial condition can be any starting point. For example, you might want to define an initial pressure or a starting balance in a bank account. In statistics, its a nuisance parameter in unit root testing . In calculus, the term usually refers to the starting condition for finding the particular solution for a differential equation.

Laplace Transforms Of Derivatives

In the rest of this chapter well use the Laplace transform to solve initial value problems for constant coefficient second order equations. To do this, we must know how the Laplace transform of \ is related to the Laplace transform of \. The next theorem answers this question.

Theorem 8.3.1

Suppose \ is continuous on \\) and of exponential order \, and \ is piecewise continuous on \.\) Then \ and \ have Laplace transforms for \ and

Proof

We know from Theorem 8.1.6 that \\) is defined for \. We first consider the case where \ is continuous on \\). Integration by parts yields

\ &= e^f-f+s\int^T_0 e^f\,dt \label \end \]

for any \. Since \ is of exponential order \, \=0\) and the integral in on the right side of Equation \ref converges as \ if \. Therefore

which proves Equation \ref.

Suppose \ and \ is only piecewise continuous on \, with discontinuities at \. For convenience, let \ and \. Integrating by parts yields

Summing both sides of this equation from \ to \ and noting that

yields Equation \ref, so Equation \ref follows as before.

Example 8.3.1:

Recommended Reading: Formal Charge Of Cf4

Use In Differential Equations

The initial condition in a differential equation is usually what is happening when the initial time is at zero . For example, lets say you have some function g, you might be given the following initial condition:

• g = 40
• g = 32

An initial condition leads to a particular solution; If you dont have an initial value, youll get a general solution.

Watch the video for two examples:

A second order differential equation with an initial condition.

initial value problem

For example, the differential equation needs a general solution of a function or series of functions :dydx = 19×2 + 10But if an initial condition is specified, then you must find a particular solution . For example:dydx19x2 + 10; y = 5.Finding a particular solution for a differential equation requires one more stepsimple substitutionafter youve found the general solution.

What Is It Initial Value

the x-axis

the y-axis

Step-by-step explanation: 1. What are the coordinates of the point that is plotted by moving 4 right from the origin and 2 down?

2 .Match each pair of coordinate points to their location on the coordinate plane.

x-value is 6 and y-value is -1

x-value is y-value is 0

x-value is 3 and y-value is 5

x-value is -4 and y-value is 5

x-value is -2 and y-value is -7

3. Which of the following statements abut the coordinate plane is true?

The origin has an x-value of 0 and any y-value.

The origin has an x-value of 0 and any y-value.

Positive y-values are above the origin.

Positive y-values are above the origin.

Negative y-values are to the right of the origin.

Negative y-values are to the right of the origin.

Negative x-values are to the right of the origin.

Negative x-values are to the right of the origin.

4. What is the horizontal or vertical distance between the points and ?

5. Select the inequality symbol that should be used to represent the following situation.

To ride the roller coaster, you must be at least 64 inches tall.

6. At least 83 students attended the play. Which inequality represents this situation?

You May Like: What Does K Mean In Physics

On Definition Of Solution Of Initial Value Problem For Fractional Differential Equation Of Variable Order

• Department of Mathematics, China University of Mining and Technology Beijing, Beijing 100083, China
• 2. School of Science, Shandong Jiaotong University, Jinan, 250357, China

• Received: 27 December 2020Accepted: 13 April 2021 22 April 2021

• MSC : 26A33

• We propose a new definition of continuous approximate solution to initial value problem for differential equations involving variable order Caputo fractional derivative based on the classical definition of solution of integer order differential equation. Some examples are presented to illustrate these theoretical results.

  Keywords:

Citation: Shuqin Zhang, Jie Wang, Lei Hu. On definition of solution of initial value problem for fractional differential equation of variable order. AIMS Mathematics, 2021, 6: 6845-6867. doi: 10.3934/math.2021401

Students Are Also Searching For

• hair would be dry and brittle without the presence of
• during which changes of state do atoms overcome the attractive forces between them?
• which of the following statements about factors of production is the most accurate?

If you have more homework to do you can use the search bar to find the answer to other homework: 40 have done it today and 15 in the last hour.

Help your mates do their homework and share Top Homework Answers with them, its completely free and easy to use!

Contents

Read Also: Geometry Segment Addition Postulate Worksheet