Examples Of Standard Deviation And How Its Used
- PERMISSION Owned by YourDictionary, Copyright YourDictionary
Standard deviation is a statistical measurement of the amount a number varies from the average number in a series. A low standard deviation means that the data is very closely related to the average, thus very reliable. A high standard deviation means that there is a large variance between the data and the statistical average, and is not as reliable. Keep reading for standard deviation examples and the different ways it appears in daily life.
Example : Distribution Of House Prices
Suppose the mean house price in neighborhood A is $250,000 and the standard deviation is $50,000. Since the standard deviation is quite large, this means that some of the house prices will be far greater than $250,000 and some will be far less. If you look at a given house in this neighborhood, theres no guarantee that the price will be close to the mean.
Conversely, suppose the mean house price in neighborhood B is also $250,000 but the standard deviation is only $10,000. Since this standard deviation is fairly small, you can be sure that any given house you look at in the neighborhood is likely to be close to this price.
If we created a boxplot to visualize the distribution of house prices in these two neighborhoods, it might look something like this:
The length of the boxplot for neighborhood A is so much greater because the standard deviation of house prices is so much higher.
In fact, house prices range from lower than $150k to higher than $400k for neighborhood A, while prices only range from about $230k to $270k for neighborhood B.
What Is Considered A Low Standard Deviation
The standard deviation is used to measure the spread of values in a sample.
We can use the following formula to calculate the standard deviation of a given sample:
2 /
- : A symbol that means sum
- xi: The ith value in the sample
- xbar: The mean of the sample
- n: The sample size
The higher the value for the standard deviation, the more spread out the values are in a sample. Conversely, the lower the value for the standard deviation, the more closely packed together the values.
One question students often have is: What is considered a low value for the standard deviation?
The answer: There is no cut-off value for what is considered a low standard deviation because it depends on the type of data youre working with.
For example, consider the following scenarios:
Scenario 1: A professor collects data on the exam scores of students in his class and finds that the standard deviation of exam scores is 7.8.
Scenario 2: An economist measures the total income tax collected by different countries around the world and finds that the standard deviation of total income tax collected is $1.2 million.
The standard deviation in scenario 2 is much higher, but thats only because the values being measured in scenario 2 are considerably higher than those being measured in scenario 1.
This means there is no single number we can use to tell whether or not a standard deviation is low or not. It all depends on the situation.
Also Check: How To Solve Math Problems With Steps
Relationship Between Standard Deviation And Mean
The mean and the standard deviation of a set of data are usually reported together. In a certain sense, the standard deviation is a “natural” measure of statistical dispersion if the center of the data is measured about the mean. This is because the standard deviation from the mean is smaller than from any other point. The precise statement is the following: suppose x1, …, xn are real numbers and define the function:
Using calculus or by completing the square, it is possible to show that has a unique minimum at the mean:
The coefficient of variation of a sample is the ratio of the standard deviation to the mean. It is a dimensionless number that can be used to compare the amount of variance between populations with means that are close together. The reason is that if you compare populations with same standard deviations but different means then coefficient of variation will be bigger for the population with the smaller mean. Thus in comparing variability of data, coefficient of variation should be used with care and better replaced with another method.
Often we want some information about the accuracy of the mean we obtained. We can obtain this by determining the standard devation of the sampled mean.The standard deviation of the mean is related to the standard deviation of the distribution by:
where N is the number of observation in the sample used to estimate the mean. This can easily be proven with:
hence
Resulting in:
Tools For Calculating Sd
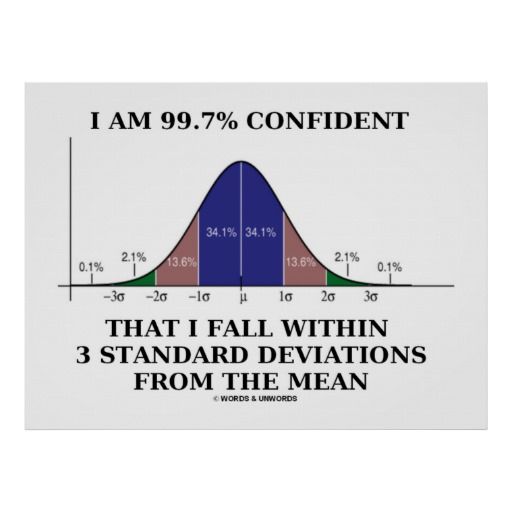
While it is helpful to understand the equations for calculating standard deviation, it would be impractical to work it out by hand for large studies. Imagine working all of this out on studies with thousands of participants. As such, it is more practical to calculate standard deviation through the help of specific tools.
For students of psychology and other social sciences, you may be familiar with SPSS which is specifically designed for data collection and analysis in research. As such, the programme has a range of tools specific to descriptive statistics such as calculating the mean and standard deviation in SPSS.
Don’t Miss: Why Is It Important To Learn Geography
Why Standard Deviation Is Important As A Measure Of Dispersion
Standard deviation is the most commonly used measure of dispersion. It is a measure of spread of data about the mean. The other advantage of SD is that along with mean it can be used to detect skewness. The disadvantage of SD is that it is an inappropriate measure of dispersion for skewed data.
S For Calculating The Standard Deviation
The standard deviation is usually calculated automatically by whichever software you use for your statistical analysis. But you can also calculate it by hand to better understand how the formula works.
There are six main steps for finding the standard deviation by hand. Well use a small data set of 6 scores to walk through the steps.
| Data set |
|---|
Don’t Miss: What Is Work Done In Physics
You Are Reading A Preview
Activate your 30 day free trial to continue reading.
Standard deviation is and index of degree of dispersion and an estimate of the variability in the population from which the sample is drawn .
Standard deviation is and index of degree of dispersion and an estimate of the variability in the population from which the sample is drawn .
Comparing Standard Deviations Between Samples
Rather than classifying a standard deviation as low or not, often we simply compare the standard deviation between several samples to determine which sample has the lowest standard deviation.
For example, suppose a professor administers three exams to his students during the course of one semester. He then calculates the sample standard deviation of scores for each exam:
- Sample standard deviation of Exam 1 Scores: 4.9
- Sample standard deviation of Exam 2 Scores: 14.4
- Sample standard deviation of Exam 3 Scores: 2.5
The professor can see that Exam 3 had the lowest standard deviation of scores among all three exams, which means the exam scores were most closely packed together for that exam.
Conversely, he can see that Exam 2 had the highest standard deviation, which means the exam scores were most spread out for that exam.
You May Like: Holt Algebra 1 Chapter 7 Cumulative Test Answers
Examples Of Standard Deviation
Unless youre sitting in a statistics class, you may think that standard deviation doesnt affect your everyday life. But youd be wrong! Even though most statisticians calculate standard deviation with computer programs and spreadsheets, its helpful to know how to do it by hand.
Here are some examples of situations that demonstrate how standard deviation is used.
How Do You Interpret Data Using Mean And Standard Deviation
More precisely, it is a measure of the average distance between the values of the data in the set and the mean. A low standard deviation indicates that the data points tend to be very close to the mean a high standard deviation indicates that the data points are spread out over a large range of values.
Also Check: Algebra 2 Unit 7 Lesson 2
Calculating Population Standard Deviation
To better explain standard deviation, lets look at a hypothetical example with five participants who were asked to complete a puzzle as quickly as they could:
| Participant |
|---|
Probability Distribution Or Random Variable
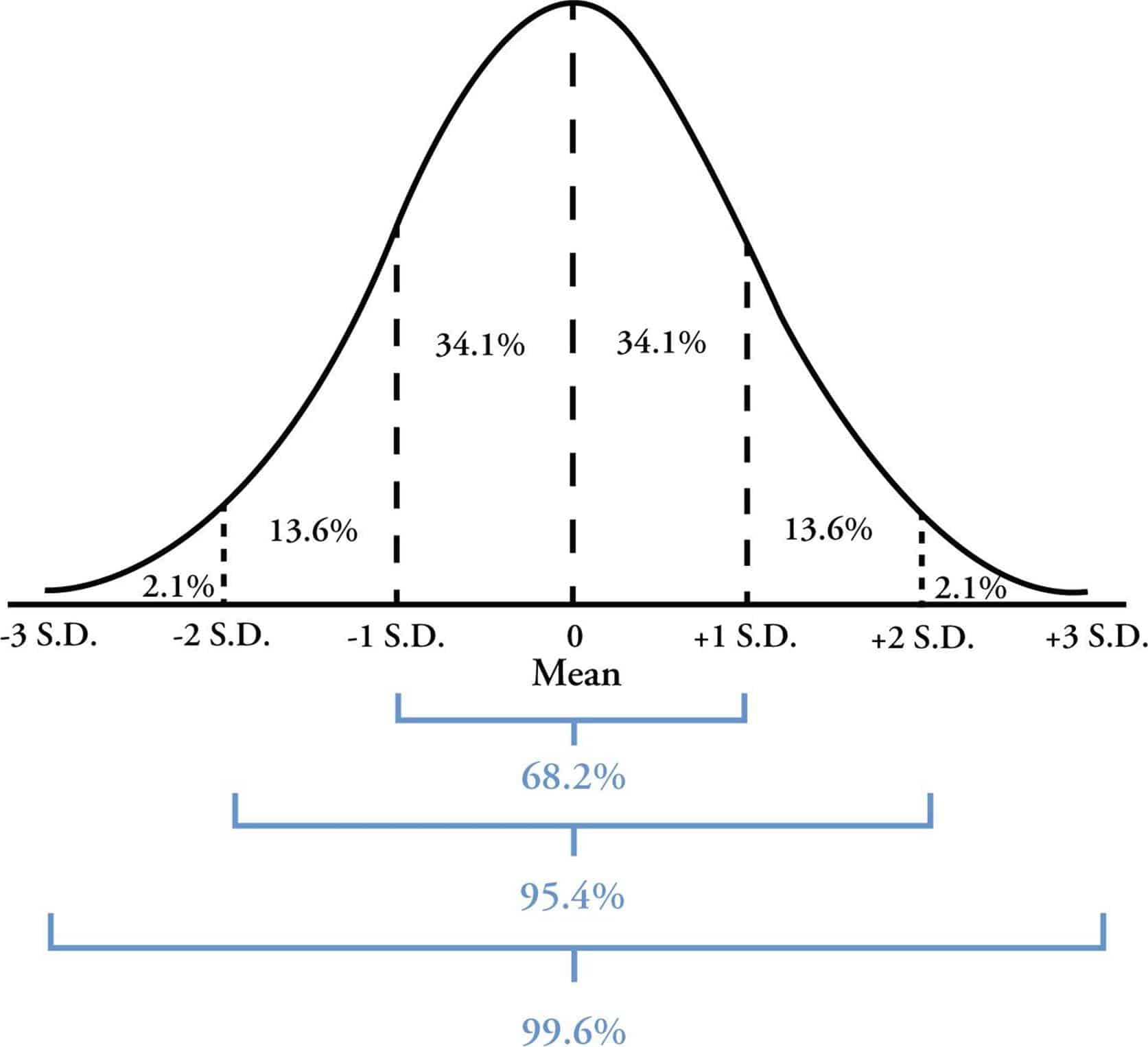
Let X be a random variable with mean value :
Here the operator E denotes the average or expected value of X. Then the standard deviation of X is the quantity
That is, the standard deviation is the square root of the average value of 2.
In the case where X takes random values from a finite data set , with each value having the same probability, the standard deviation is
or, using summation notation,
The standard deviation of a probability distribution is the same as that of a random variable having that distribution. Not all random variables have a standard deviation, since these expected values need not exist. For example, the standard deviation of a random variable which follows a Cauchy distribution is undefined because its expected value is undefined.
Don’t Miss: What Jobs Can You Get With Geography
What Does The Z
A z-score describes the position of a raw score in terms of its distance from the mean, when measured in standard deviation units. The z-score is positive if the value lies above the mean, and negative if it lies below the mean.
It is also known as a standard score, because it allows comparison of scores on different kinds of variables by standardizing the distribution. A standard normal distribution is a normally shaped distribution with a mean of 0 and a standard deviation of 1 .
Figure 1. A standard normal distribution .
Identities And Mathematical Properties
The standard deviation is invariant to changes in location, and scales directly with the scale of the random variable. Thus, for a constant c and random variables X and Y:
The standard deviation of the sum of two random variables can be related to their individual standard deviations and the covariance between them:
where stand for variance and covariance, respectively.
The calculation of the sum of squared deviations can be related to moments calculated directly from the data. In general, we have
For a finite population with equal probabilities on all points, we have
Thus, the standard deviation is equal to the square root of .See computational formula for the variance for a proof of this fact, and for an analogous result for the sample standard deviation.
Recommended Reading: What Is Locomotion In Biology
Using The Coefficient Of Variation
One way to determine if a standard deviation is low is to compare it to the mean of the dataset.
A coefficient of variation, often abbreviated CV, is a way to measure how spread out values are in a dataset relative to the mean. It is calculated as:
CV = s / x
- s: The standard deviation of dataset
- x: The mean of dataset
The lower the CV, the lower the standard deviation relative to the mean.
For example, suppose a professor collects data on the exam scores of students and finds that the mean score is 80.3 and the standard deviation of scores is 7.8. The CV would be calculated as:
- CV: 7.8 / 80.3 = .097
Suppose another professor at a different university collects data on the exam scores of his students and finds that the mean score is 70.3 and the standard deviation of scores is 8.5. The CV would be calculated as:
- CV: 8.5 / 90.2 = 0.094
Although the standard deviation of exam scores is lower for the first professors students, the coefficient of variation is actually higher than that of the exam scores for the second professors students.
This means the variation of exam scores relative to the mean score is higher for the first professors students.
Why Is Standard Deviation Important
The standard deviation is used to measure the spread of values in a sample.
We can use the following formula to calculate the standard deviation of a given sample:
2 /
- : A symbol that means sum
- xi: The ith value in the sample
- xbar: The mean of the sample
- n: The sample size
The higher the value for the standard deviation, the more spread out the values are in a sample. Conversely, the lower the value for the standard deviation, the more tightly packed together the values.
One question students often have is: Why is the standard deviation important?
The answer: Standard deviation is important because it tells us how spread out the values are in a given dataset.
Whenever we analyze a dataset, were interested in finding the following metrics:
- The center of the dataset. The most common way to measure the center is with the mean and the median.
- The spread of values in the dataset. The most common way to measure spread is with the standard deviation.
The following examples illustrate the importance of the standard deviation in practice.
Read Also: What Is Closure In Psychology
What Is Standard Deviation
Standard deviation measures the spread of data relative to its mean. You can think of standard deviation as the average distance between a single data point and the mean. A large standard deviation shows that data is more widely dispersed about the mean, and a small standard deviation shows that data are tightly clustered around the mean. You can calculate standard deviation by taking the square root of the variance.
With Sample Standard Deviation
The most common estimator for used is an adjusted version, the sample standard deviation, denoted by “s” and defined as follows:
where is the sample and is the mean of the sample. This correction is known as Bessel’s correction. The reason for this correction is that s2 is an unbiased estimator for the variance 2 of the underlying population, if that variance exists and the sample values are drawn independently with replacement. However, s is not an unbiased estimator for the standard deviation it tends to underestimate the population standard deviation.
Note that the term “standard deviation of the sample” is used for the uncorrected estimator whilst the term “sample standard deviation” is used for the corrected estimator . The denominator N 1 is the number of degrees of freedom in the vector of residuals,.
Read Also: Geometry Definition Of Skew Lines
Example Of Standard Deviation Of Samples
This follows the same calculation as the example above, for standard deviation for population, with one exception: The division should be “N – 1” not “N”.
=
Then it follows the same example as above, except that there is a 4 where there was a 5.
Write the formula.
=
How many numbers are there ?
There are five numbers.
The mean of this data is / 5 = 120.
=
What are the respective deviations from the mean?
The deviation from the mean is given by 96 – 120 = -24 104 – 120 = -16 126 – 120 = 6 134 – 120 = 14 and 140 – 120 = 20.
=
=
Square and sum the deviations:
The sum of their squares is given by 2 + 2 + 2 + 2 + 2 = 1464.
=
=
=
Divide by the number of scores minus one :
The mean of this value is given by 1464 / 4 = 366. The number in between the brackets is the variance of the data.
=
To calculate standard deviation, we take the square root = 19.13.
= 19.13
Playing The Odds Of Mathematics
Standard deviation is an important part of any statistical analysis. But its just one part of a wider study that includes probability exercises as well. Check out these examples of probability to further increase your mathematical understanding. You can also apply standard deviation to these random sampling exercises.
You May Like: Mastery Education Answer Key Algebra 1
Example : Distribution Of Salaries
Suppose the mean salary at company A is $80,000 and the standard deviation is $20,000. Since the standard deviation is so large, theres no guarantee that you will get paid close to $80,000 per year if you work at this company since theres such a variation in salaries.
Conversely, suppose the mean salary at company B is also $80,000 but the standard deviation is only $4,000. Since this standard deviation is so small, you can be sure that youll get paid close to $80,000 because theres very little variation in salaries.
If we created a boxplot to visualize the distribution of salaries at these two companies, it might look something like this:
Notice that the length of the boxplot for company A is so much greater because the standard deviation of salaries is so much higher.
Both companies have the same mean salary, but the spread of salaries is much higher at company A.