Can Skew Lines Be Perpendicular
In a math textbook for primary school, there’s a picture like the one below. They explain which of the line segments are perpendicular and which are parallel to AD.
There’s also a note stating that A1B1, D1C1, BB1 and CC1 are neither parallel nor perpendicular to AD.
I was wondering about that statement, because I learned that those four are perpendicular to AD. So I wrote to the book publisher asking about that. They replied that actually there are two conventions for this situation and they choose “not perpendicular” which, according to them, is more popular.
Is there really no consensus on that?
Edit:I found another question here, related to a mathematical consensus: Is $0$ a natural number? and I’d accept an answer referring to some resources and clarifying whether the consensus exists or not.
The Distance Between Skew Lines
Look at the figure below. You can see two lines from the three-dimensional Cartesian plane. As is evident from the figure, the shortest distance between the lines is one which is perpendicular to both the lines as compared to any other lines that joins these two skew lines.
We will now move on to how the shortest distance i.e. the length of the perpendicular to two skew lines can be calculated in Vector form and in Cartesian form.
Applications Of Skewed Data
Skewed data arises quite naturally in various situations. Incomes are skewed to the right because even just a few individuals who earn millions of dollars can greatly affect the mean, and there are no negative incomes. Similarly, data involving the lifetime of a product, such as a brand of light bulb, are skewed to the right. Here the smallest that a lifetime can be is zero, and long lasting light bulbs will impart a positive skewness to the data.
Don’t Miss: Which Csu Has The Best Biology Program
Examples Of Skew In A Sentence
skewingskewingskew WSJskew Quartzskew Timeskew alskew Forbesskew San Francisco Chronicleskew Varietyskew Washington Postskew San Francisco Chronicleskew The Atlanticskew Star Tribuneskew Forbesskew The Atlanticskew Rolling Stoneskew San Francisco Chronicleskew The Atlanticskew Los Angeles Timesskew orlandosentinel.comskew Varietyskew The Indianapolis StarskewForbesskew Forbesskew National Reviewskew Forbes
These example sentences are selected automatically from various online news sources to reflect current usage of the word skew. Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Definition Of Line Segment
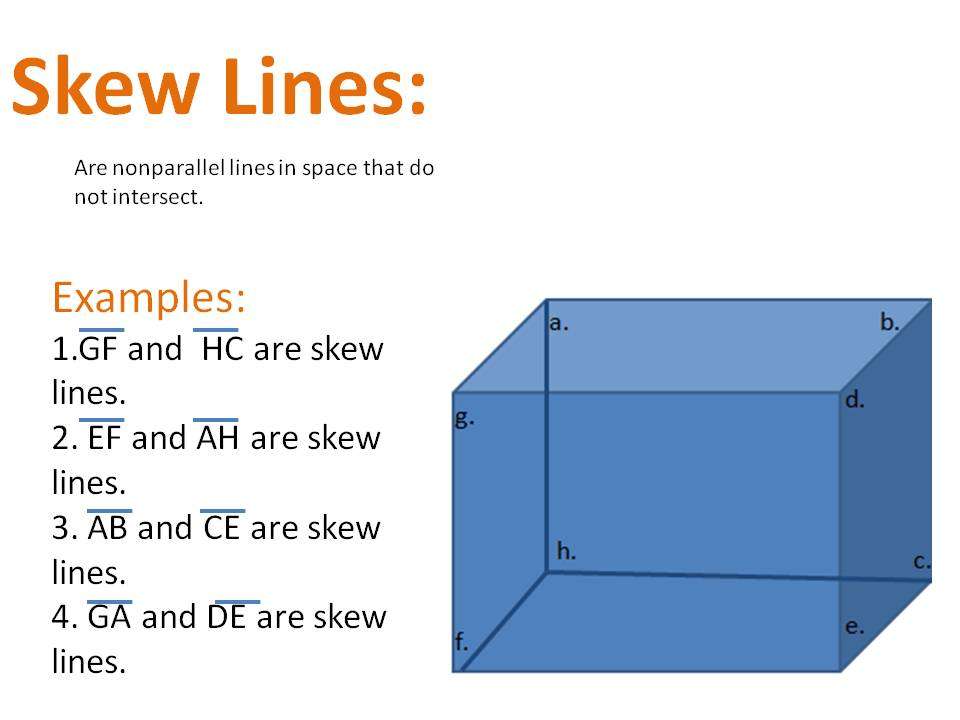
In mathematics, line segment and line are essential concepts for constructing geometrical shapes. In geometry, a line segment is the part of the line with a fixed distance. We can say that the line segment has a finite length, whereas the line does not have any fixed size.
As per Euclids concept, a line is a breadthless length. A line is an essential geometric figure, which connects all points on it. A line has no endpoints, and it extends infinitely in both directions. A line segment is a part of the line. A line segment connects any of the two points on the line. The part or portion of the line between points \ and \ is called the line segment in the figure below. Thus, \ is the line segment.
The line segment is connected way of the two points, which you can measure. Line segments are utilised to form the sides of the polygon.
Don’t Miss: What Is Protein Synthesis In Biology
Solved Example For You
Question 1: Find the shortest distance between the lines whose equations are:
$$ \vec_1 = \vec + \vec + \lambda $$
$$ \vec_2 = 2 \vec + \vec \vec+ \mu $$
Answer: We shall compare the given equations with the standard form i.e. \vec_1 = \vec_1 + \lambda \vec_1 and vec_2 = \vec_2 + \mu \vec_2. Accordingly, we have:
$$ a_1 = \vec + \vec , b_1 = 2 \vec \vec + \vec $$
$$ a_2 = 2 \vec + \vec \vec , b_2 = 3\vec 5 \vec + 2 \vec $$
So, we can find the shortest distance as :
$$ d = | . | / | \times | $$
= | 3 0 + 7 | / 1/2
= |10| / 1/2 is the shortest distance between the given lines.
Question 2: How does the skew lines look like?
Answer: The skew lines are those lines which do not intersect, but also never lie on a similar plane. They look like they are running in similar directions and even look totally random.
Question 3: Can skew lines be perpendicular?
Answer: A line is said to be perpendicular to the other line only if they are intersecting at a right angle, and we know that the skew lines never intersect or meet, so, the skew lines can never become a perpendicular.
Question 4: What are the dissimilarities between the parallel lines and the skew lines?
Answer: The most common difference between the parallel lines and the skew lines is that the parallel lines lie in a similar plane whereas the skew lines lie in dissimilar planes.
Question 5: How can we prove the skew lines?
Line: Definition Diagrams Types And Examples
In geometry, it is common to say a line segment and lines are the same. A Line segment has a definite beginning and a definite end, but a line is extended towards infinity at both ends. Examples of line segments include the length of a table, the distance of a straight road, etc. A segment is part of a line, but a line is not part of a segment. Lets learn about lines, their types and some real-life examples.
Horizontal, vertical lines, parallel and perpendicular lines are examples of different types of lines. A line is a one-dimensional figure, which has length but no width. A line is made up of a series of points that are infinitely stretched in opposite directions. Two points in a two-dimensional plane determine it. Collinear points are two points that are located on the same line. Continue reading this article to know more about Line.
| Latest Update:? The CBSE Term 1 results are expected to be released in January 2022.? The Term 2 examination will commence in March/April. The board will soon release the admit card and exam date sheet in February 2022. |
Recommended Reading: How To Apply For Phd In Psychology
What Are Skew Lines
Before learning about skew lines, we need to know three other types of lines. These are given as follows:
- Intersecting Lines – If two or more lines cross each other at a particular point and lie in the same plane then they are known as intersecting lines.
- Parallel Lines – If two are more lines never meet even when extended infinitely and lie in the same plane then they are called parallel lines.
- Coplanar Lines – Coplanar lines lie in the same plane.
Skew Lines And Ruled Surfaces
If one rotates a line L around another line L’ skew but not perpendicular to it, the swept out by L is a . For instance, the three hyperboloids visible in the illustration can be formed in this way by rotating a line L around the central white vertical line L’. The copies of L within this surface make it a it also contains a second family of lines that are also skew to L’ at the same distance as L from it but with the opposite angle. An of this ruled surface produces a surface which in general has an elliptical cross-section rather than the circular cross-section produced by rotating L around L’ such surfaces are also called hyperboloids of one sheet, and again are ruled by two families of mutually skew lines. A third type of ruled surface is the . Like the hyperboloid of one sheet, the hyperbolic paraboloid has two families of skew lines in each of the two families the lines are parallel to a common plane although not to each other. Any three skew lines in R3 lie on exactly one ruled surface of one of these types .
Don’t Miss: What Is Density In Physics
Shortest Distance Between Two Skew Lines
The shortest distance between two skew lines is given by the line that is perpendicular to the two lines as opposed to any line joining both the skew lines.
The vector equation is given by d = |\}}\times\overrightarrow}|}\)| is used when the lines are represented by parametric equations
The cartesian equation is d = \ is used when the lines are denoted by the symmetric equations.
Parallel And Skew Lines
Parallel lines are two lines in the same plane that remain at a constant distance from each other and never intersect.In a coordinate plane, parallel lines can be identified as having equivalent slopes. Parallel lines aretraditionally marked in diagrams using a corresponding number of chevrons .
Skew lines are two lines not in the same plane that do not intersect. Parallel and skew lines are also important concepts in Algebra and upper-level math courses.
What are intersecting and parallel lines?Intersecting lines are coplanar.Three points determine a plane.Parallel lines never intersect and are coplanar.
What are skew lines?Skew lines are noncoplanar and nonintersecting.
Learn what parallel, skew and intersecting lines are.Parallel lines are two line in the same plane that do not intersect.
Students learn the definitions of parallel lines, skew lines.Skew lines are non-coplanar lines that do not intersect.
Parallel Planes and LinesIn Geometry, a plane is any flat, two-dimensional surface. Two planes that do not intersect are said to beparallel. Parallel planes are found in shapes like cubes, which actually has three sets of parallel planes.The two planes on opposite sides of a cube are parallel to one another.
Two lines in the same plane either intersect or are parallel. If two lines intersect and form a right angle,the lines are perpendicular.
Skew lines are lines that are non-coplanar and do not intersect.
Example:
Read Also: What Is Density In Geography
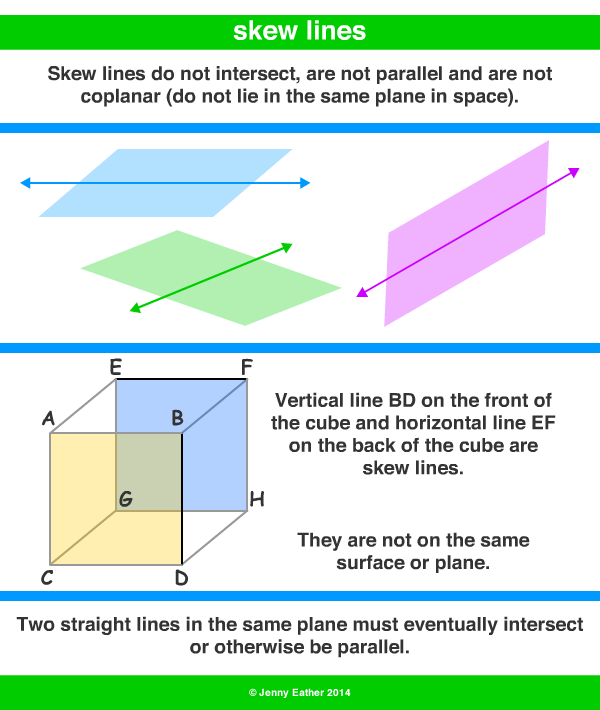
Distance Between Skew Lines
The shortest distance between two skew lines is the length of the line segment that intersects both lines and is perpendicular to both lines. For each pair of skew lines, there is only one line segment that is perpendicular to and intersects both lines.
In the figure above, line segment CD is perpendicular to both lines a and b so its length is the shortest distance between the skew lines a and b above.
Distance Between Skew Lines Formula
To find the distance between the two skew lines, we have to draw a line that is perpendicular to these two lines. We can represent these lines in the cartesian and vector form to get different forms of the formula for the shortest distance between two chosen skew lines.
Say we have two skew lines P1 and P2. We will study the methods to find the distance between two skew lines in the next section.
You May Like: Common Core Algebra 1 Unit 2 Lesson 5 Homework Answers
Test For Perpendicular First Then Intersecting And Then Skew
Example
Say whether the lines are parallel, intersecting, perpendicular or skew.
Well start by testing the lines to see if theyre parallel by pulling out the coefficients
???\frac=\frac=\frac???
???\frac53=\frac12=\frac???
Since ???5/3\neq1/2\neq-1/2???, we know the lines are not parallel.
Because theyre not parallel, well test to see whether or not theyre intersecting. Well set the equations for ???x???, ???y???, and ???z??? from each line equal to each other. If we can find a solution set for the parameter values ???s??? and ???t???, and this solution set satisfies all three equations, then weve proven that the lines are intersecting.
Setting ???x_1=x_2???, we get
???x_1=x_2???
Setting ???z_1=z_2???, we get
???z_1=z_2???
???0=7???
Since ???0\neq7???, the lines are not intersecting.
Because ???L_1??? and ???L_2??? are not parallel and not intersecting, by definition they must be skew.
Two lines are intersecting if the lines are not parallel or if you can solve them as a system of simultaneous equations.
In the previous example, we didnt test for perpendicularity because only intersecting lines can be perpendicular, and we found that the lines were not intersecting. If we had found that ???L_1??? and ???L_2??? were in fact perpendicular, we would have needed to test for perpendicularity by taking the dot product, like this:
???L_1\cdot L_2=++???
Read Also: Which Founding Contributors To Psychology Helped Develop Behaviorism
Skew Flats In Higher Dimensions
In higher-dimensional space, a flat of dimension k is referred to as a k-flat. Thus, a line may also be called a 1-flat.
Generalizing the concept of skew lines to d-dimensional space, an i-flat and a j-flat may be skew if i + j< d. As with lines in 3-space, skew flats are those that are neither parallel nor intersect.
In affine d-space, two flats of any dimension may be parallel.However, in projective space, parallelism does not exist two flats must either intersect or be skew.Let I be the set of points on an i-flat, and let J be the set of points on a j-flat.In projective d-space, if i + j d then the intersection of I and J must contain a -flat.
In either geometry, if I and J intersect at a k-flat, for k 0, then the points of I J determine a -flat.
Also Check: How Can Your Environment And Geography Impact Your Economic Activity
What Are Skew Lines In Geometry Slidesharedocs
Skew Lines Activity. Here are a number of highest rated Skew Lines Activity pictures on internet. We identified it from well-behaved source. Its submitted by giving out in the best field. We agree to this nice of Skew Lines Activity graphic could possibly be the most trending topic taking into consideration we portion it in google plus or facebook.
Real World Geometry Three Or More Coplanar Parallel Lines, Skew Lines Geometry Help Youtube, Pointslinesplanesrays Segments And Parallel Perpendicular And Skew, ,
Sgi.gene.com.gene.com is an open platform for users to share their favorite wallpapers, By downloading this wallpaper, you agree to our Terms Of Use and Privacy Policy. This image is for personal desktop wallpaper use only, if you are the author and find this image is shared without your permission, DMCA report please Contact Us
Can Lines On Different Planes Be Parallel
In Geometry, a plane is any flat, two-dimensional surface. Two planes that do not intersect are said to be parallel. Parallel planes are found in shapes like cubes, which actually has three sets of parallel planes. But a line and plane can be parallel to each other and two planes can be parallel to each other.
Read Also: What Is Cardinal Direction In Geography
Measures Of Shape: Skewness And Kurtosis
Summary:measures of shapeskewness tells you the amount and direction of skewkurtosis tells you how tall and sharp the central peak is
Why do we care? One application istesting for normality: many statistics inferences require thata distribution be normal or nearly normal. A normal distribution hasskewness and excess kurtosis of 0, so if your distribution is close tothose values then it is probably close to normal.
Technology:
- MATH200B Program Extra Statistics Utilities for TI-83/84 has a program to download toyour TI-83 or TI-84. Among other things, the program computesall the skewness and kurtosis measures in this document.
- Theaccompanying Excel workbookperforms two tests for normality, including theDAgostino-Pearson test described below.
Contents:
What Is A Skew Angle
The term angle of skew or skew angle is basically the angle between a normal/perpendicular to the alignment/centerline of the bridge and the centerline of the pier . Thus, on a straight bridge, the skew angle at all supports would normally be the same and the term skew angle can be applied to the bridge as a whole
Dont Miss: What Is The Molecular Geometry Of Ccl4
Also Check: Who Established The First Psychological Laboratory
Different Types Of Lines In Geometry Basic Definition And Examples
A line is a one-dimensional geometric figure having length but no width. It is made up of points that are extended in opposite directions infinitely. The different types of lines are horizontal, vertical, parallel, perpendicular, curved, and slanting lines. The definitions of each type of line with an image are given below. Go through the entire article to learn in detail about the Types of Lines in Geometry and examples for each one of them.
What Is The Definition Of Skew In Math
geometryskewskew
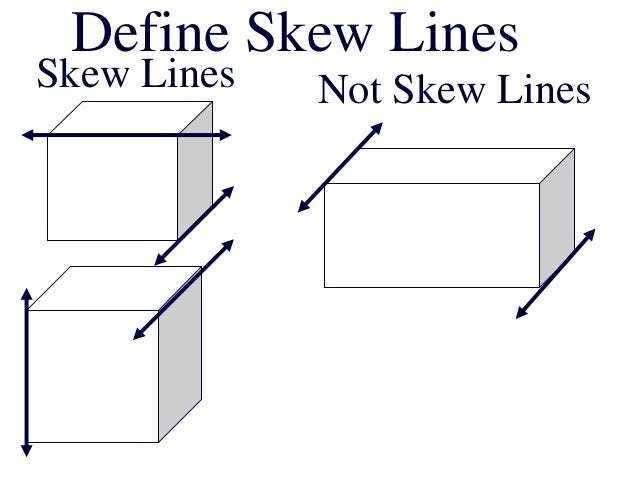
. Likewise, what is skew lines with examples?
Skew lines are straight lines in a three dimensional form which are not parallel and do not cross. An example of skew lines are the sidewalk in front of a house and a line running across the top edge of a side of a house.
Secondly, are skew lines perpendicular? Skew lines are lines that are in different planes and never intersect. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Learn skew line, parallel and perpendicular lines along with skew line exmaples with the help of resources on this page.
Consequently, which definition best describes skew lines?
Skew lines are two lines that do not intersect and are not parallel. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions . Two lines are skew if and only if they are not coplanar .
Are parallel lines coplanar?
Two lines are parallel lines if they are coplanar and do not intersect. Lines that are not coplanar and do not intersect are called skew lines. Two planes that do not intersect are called parallel planes.
You May Like: Countdown To The Algebra 1 Eoc Answer Key
Also Check: Is Anthrax Biological Or Chemical
Asset Prices As Examples Of A Skewed Distribution
The departure from normal returns has been observed with more frequency in the last two decades, beginning with the internet bubble of the late 1990s. In fact, asset returns tend to be increasingly right-skewed. This volatility occurred with notable events, such as the Sept. 11 terrorist attacks, the housing bubble collapse and subsequent financial crisis, and during the years of quantitative easing .
The unwinding of the Federal Reserve Boards unprecedented easy monetary policy may be the next chapter of volatile market action and more asymmetrical distribution of investment returns. Most recently we saw extreme downside moves during the beginning of the global COVID-19 pandemic.