What Is A Rate
Ratios and Rates. Rates are ratios, any ratio with different units in the numerator and denominator is called a rate. To solve most questions involving rates of all kinds, all we have to do is to set up an equation of the form ratio = ratio. We just match the units on each side.
Image by BortN66
Remember that in such an equation, fraction equals fraction or ratio = ratio is called a proportion. And if youre not familiar with it, it may be a good idea to go back and look at the video, Operations with Proportions. What you can do and cant do with a proportion mathematically, that video is in the fraction module.
Some Rates You Should Know
Rates are often expressed as so many units per units. So for example, all of these are rates. Many of these are drawn from science. The last two are a special kind, 60 minutes per hour or 360 degrees per revolution, these are examples of unit conversions. So these would be examples of things you would actually be expected to know.
The other ones you would not be expected to know. But you would be expected to know that there are 60 minutes in an hour, and you can write this as a ratio. We would set this given rate equal to a fraction with the same units in the numerator and the denominator. So either the problem itself would give you one of the rates, for example, one of the blue rates.
Or you would know yourself something about the units in the way that the units are related. You set that up as a ratio, and then you set that equal to a fraction on the other side that matches the same units in the numerator and the denominator.
Computer Era And Iterative Algorithms
- . +b_)^}}}.}
The development of computers in the mid-20th century again revolutionized the hunt for digits of . Mathematicians John Wrench and Levi Smith reached 1,120 digits in 1949 using a desk calculator. Using an inverse tangent infinite series, a team led by George Reitwiesner and John von Neumann that same year achieved 2,037 digits with a calculation that took 70 hours of computer time on the ENIAC computer. The record, always relying on an arctan series, was broken repeatedly until 1 million digits were reached in 1973.
Two additional developments around 1980 once again accelerated the ability to compute . First, the discovery of new iterative algorithms for computing , which were much faster than the infinite series and second, the invention of fast multiplication algorithms that could multiply large numbers very rapidly. Such algorithms are particularly important in modern computations because most of the computer’s time is devoted to multiplication. They include the Karatsuba algorithm, ToomCook multiplication, and Fourier transform-based methods.
Recommended Reading: Figure-ground Psychology
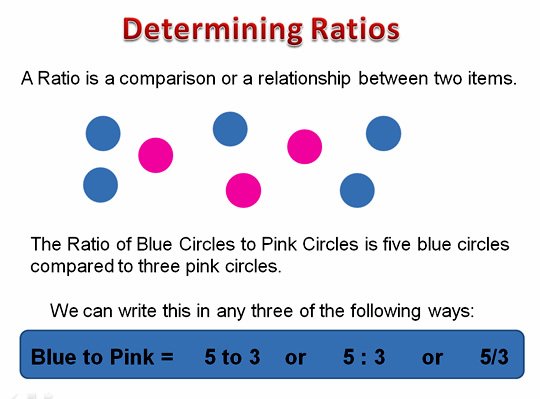
What Is A Ratio
In mathematics, a ratiois a comparison of two or more numbers that indicates their sizes in relation to each other. A ratio compares two quantities by division, with the dividend or number being divided termed the antecedent and the divisor or number that is dividing termed the consequent.
Example: you have polled a group of 20 people and found that 13 of them prefer cake to ice cream and 7 of them prefer ice cream to cake. The ratio to represent this data set would be 13:7, with 13 being the antecedent and 7 the consequent.
A ratio might be formatted as a Part to Part or Part to Whole comparison. A Part to Part comparison looks at two individual quantities within a ratio of greater than two numbers, such as the number of dogs to the number of cats in a poll of pet type in an animal clinic. A Part to Whole comparison measures the number of one quantity against the total, such as the number of dogs to the total number of pets in the clinic. Ratios like these are much more common than you might think.
How To Use Scale Factor
Scaling an object helps you visualize large real-world objects in small spaces or enlarge a small object for better viewing. Scale factor is how we ensure the representation of the object differs only in size from the original object.
We use scale to:
- Draw similar figures in geometry
- Make scale models
- Draw scale blueprints of architecture and machinery
A common real-world use of scale factor is to bring vast areas of land down to small pieces of paper, like on a map.
Scale is used to allow designers, architects, and machinists to handle models of objects that would be too big to keep on a if they were actual size.
Don’t Miss: What Does Abiotic Mean In Biology
How To Find Scale Factor
To find the scale factor, you first decide which direction you are scaling:
| Scale Up | = |
| Scale Down | = |
The scale factor for scaling up is a ratio greater than 1 . The scale factor for scaling down is a ratio of less than 1 .
Once you know which way you are scaling, you compare corresponding sides using the correct basic equation. Compare the side length of the real object to the length of the corresponding side in the representation.
Role And Characterizations In Mathematics
Because is closely related to the circle, it is found in many formulae from the fields of geometry and trigonometry, particularly those concerning circles, spheres, or ellipses. Other branches of science, such as statistics, physics, Fourier analysis, and number theory, also include in some of their important formulae.
You May Like: Unit 1 Test Geometry Basics Answers Key
What Is Unit Rate Definition
A unit rate is defined as a ratio that compares the first quantity to one unit of the second quantity. The two quantities being compared have different units. For example, if a person types 500 words in an hour, then it is expressed as 500 words per hour or 500 words/hour. Here, we can observe that the denominator is 1.
What Is The Definition Of Unit Ratio In Math
4.8/5unit ratioratioratiounit ratio
Considering this, what is a unit ratio in math?
A unit rate is a ratio that has a denominator of 1. A unit rate is also called a unit ratio. . For example, 10 feet per second or 35 miles per hour, are unit rates . Any ratio can be converted into a unit ratio by dividing the numerator by the denominator.
Additionally, whats is a unit? A unit is any measurement that there is 1 of. So 1 meter is a unit. And 1 second is also a unit. And 1 m/s is also a unit, because there is one of it.
Considering this, what is a unit rate simple definition?
A rate is a ratio that is used to compare different kinds of quantities. A unit rate describes how many units of the first type of quantity corresponds to one unit of the second type of quantity. Some common unit rates are miles per hour, cost per item, earnings per week, etc.
Can a ratio have units?
Ratios have no unitsA ratio is how many times bigger one thing is than another. It’s a number you multiply by to get one thing from another. But remember, when you find the ratio of two quantities, they must be in the same units.
Read Also: Example Of Span Linear Algebra
How To Use Ratios In Math
- B.B.A., Finance and Economics, University of Oklahoma
Ratios are a helpful tool for comparing things to each other in mathematicsand real life, so it is important to know what they mean and how to use them. These descriptions and examples will not only help you to understand ratios and how they function but will also make calculating them manageable no matter what the application.
Finding Scale Factor Of Similar Figures
Here are two similar triangles. What is the scale factor used to create the second, larger figure?
Since we are scaling up, we divide the larger number by the smaller number:
. To go from legs of 12 3 .
Now, let’s try to scale down. Here are two similar pentagons. What is the scale factor used to create the second, smaller figure?
Because we are scaling down, we divide corresponding side lengths :
. To get the second, smaller figure, we multiply 21 the figure on the right uses a scale factor of 1 h .
Let’s look at one more example and scale both up and down. Consider these two similar right triangles with labeled sides.
If we have the little right triangle above and want to scale it up to the larger triangle, we write this:
So every other linear measure is multiplied times 5 .
If we have the big right triangle and want to scale it down to make the smaller one, we write this:
So every other linear measure is multiplied times 1 5
Don’t Miss: How To Find Ksp Chemistry
How To Reduce A Shape By A Scale Factor
Suppose you are given a figure and told to reduce it by 25 . Think in steps:
Suppose we have a rectangle that is 16 wide and we need to reduce it by 25
That means it will be 75
Now, we simplify our answer:
The width of our smaller new shape must be 12 . We repeat these steps with the other dimension, 6
The height of our smaller rectangle must be 4.5 .
In The Mandelbrot Set
An occurrence of in the fractal called the Mandelbrot set was discovered by David Boll in 1991. He examined the behaviour of the Mandelbrot set near the “neck” at . When the number of iterations until divergence for the point is multiplied by , the result approaches as approaches zero. The point at the cusp of the large “valley” on the right side of the Mandelbrot set behaves similarly: the number of iterations until divergence multiplied by the square root of tends to .
Don’t Miss: Copulation Biology
What Is The Definition Of Rate In Math
Rate is usually defined as a ratio of two quantities with different units. Usually, the rate is written as a fraction, with the first quantity as the numerator and the second quantity as the denominator. We can express the rate by reducing them to the lowest form possible. For example, if a person takes 30 steps in 20 seconds, then the rate at which they walk is 30 steps/20 seconds or 3 steps/2 seconds.
Proportions And Percentage Ratios
If we multiply all quantities involved in a ratio by the same number, the ratio remains valid. For example, a ratio of 32 is the same as 128. It is usual either to reduce terms to the lowest common denominator, or to express them in parts per hundred .
If a mixture contains substances A, B, C and D in the ratio 5942 then there are 5 parts of A for every 9 parts of B, 4 parts of C and 2 parts of D. As 5+9+4+2=20, the total mixture contains 5/20 of A , 9/20 of B, 4/20 of C, and 2/20 of D. If we divide all numbers by the total and multiply by 100, we have converted to percentages: 25% A, 45% B, 20% C, and 10% D .
If the two or more ratio quantities encompass all of the quantities in a particular situation, it is said that “the whole” contains the sum of the parts: for example, a fruit basket containing two apples and three oranges and no other fruit is made up of two parts apples and three parts oranges. In this case, 2 , or 40% of the whole is apples and 3 5 }} , or 60% of the whole is oranges. This comparison of a specific quantity to “the whole” is called a proportion.
Read Also: Does Elton John Have Biological Children
What Is Simple Interest Rate Definition
In the context of simple interest, rate is defined as the percentage of the money that is paid by a borrower to a lender on a per annum basis. For example, if a person borrows $1000 dollars on a rate of interest of 10%, then at the end of a year, the amount to be paid back to the lender is $1100. Here, 10% is the rate of interest.
Where Does Ratio Come From
You might remember from math class that a ratio is a proportional relationship between two numbers. For example, if I have two carrots for every one apple, my carrot-to-apple ratio is 2:1, or 2/1 as a fraction.
In the Twittersphere, a ratio specifically refers to the number of replies to a tweet versus the number of likes and retweets. The importance of this ratio was first called out by user @85mf, who noted on March 7, 2017 that U.S. congressman Jason Chaffetz had a tweet with 701 replies and only 23 retweets and 108 likes. @85mf commented: Nothing on this site makes me happier than reply-to-RT ratios like this. That is the ratio of someone who fuuuuu***d up.
In April 2017, an article in Esquire, How to Know If Youve Sent a Horrible Tweet: A Deep Dive into The Ratio, gave a longer description of this phenomenon. Essentially, showing you like something on Twitter is easy: You simply like or retweet the comment. It takes more effort, however, to leave a negative comment, so, if lots of people do so, then it must be a sign the tweet has really stepped in it. By fall 2017, the noun ratio had been verbed, as in Ive been ratioed or Lets ratio this guy.
Before Twitter analytics became a thing, having something that was well-ratioed, like ingredients on a sandwich, meant it was well-proportioned. But since 2017, there is little positive about being ratioed. It means your tweet has been taken down by the hive mind.
Don’t Miss: How To Find Ksp In Chemistry
Converting Ratio To Percentage
A number that is expressed as a percentage can be seen as a type of ratio since the number to the left of the percent sign is being compared to 100. You can convert a ratio to a percentage by first converting the ratio to a fraction, then dividing the numerator of the fraction by the denominator and then multiplying by 100. For example:
Now multiply by 100 to turn this into a percentage:
To convert a percentage to a ratio, first create a fraction with 100 in the denominator. Simplify the fraction and then form the ratio by placing the numerator to the left of the ratio sign and the denominator to the right.
For more information on ratios, watch the video below:
Related Articles
It’s Easy To Get Ratios Backwards
If you know that John and Jim have weights in the ratio 1.2 : 1, there can be confusion about whom is the heavier of the two. By convention we assume that since John is mentioned first then his weight is the 1.2 in the ratio since that is also first. But you should be as explicit as you can. It is better to say John’s weight is 1.2 times Jim’s.
When the ratio is expressed as a fraction, the convention is that the first mentioned item is on top .
Read Also: Geometry Unit 4 Quiz Answer Key
Basic Concept Of Ratios
We will discuss here about the basic concept of ratios.
Definition: The ratio of two like quantities a and b is thefraction \, which indicates how many times b is the quantity a.In other words, their ratio indicates their relative sizes.
If x and y are two quantities of the same kind and with thesame units such that y 0 then the quotient \ is called theratio between x and y.
Let the weights of two persons be 40 kg and 80 kg. Clearly,the weight of the second person is double the weight of the first personbecause 80 kg = 2 × 40 kg.
Therefore, \ = \ = \.
We say, the ratio of the weight of the first person to theweight of the second person is \ or 1 : 2.
The ratio of two like quantities a and b is the quotient a ÷ b, and it is written as a : b .
In the ratio a : b, a and b are called terms of the ratio, a is called the antecedent or first term, and b is called the consequent or second term. Then, ratio of two quantities = antecedent : consequent.
Example: The ratio of heights of two persons A and B whose heights are 6 ft and 5 ft is \, i.e., \ or 6 : 5. Here, 6 is the antecedent and 5 is the consequent.
Ratio and proportion
Solved Questions On Ratio And Proportion

1. Are the Ratios 4:5 and 5:10 said to be in Proportion?
Solution:
Expressing the given ratios 4:5 we have 4/5 = 0.8
5:10 = 5/10 = 0.2
Since both the ratios are not equal they are not in proportion.
2. Out of the total students in a class, if the number of boys is 4 and the number of girls being 5, then find the ratio between girls and boys?
Solution:
The ratio between girls and boys is 5:4. The ratio can be written in factor form as 5/4
3. Two numbers are in the ratio 3 : 4. If the sum of numbers is 42, find the numbers?
Solution:
Given 3/4 is the ratio of any two numbers
Let us consider the numbers be 3x and 4x
Given, 3x+4x = 42
You May Like: How To Login To Imagine Math