When To Calculate Probabilities
While there are some kind of probability calculations underlying all statistical tests, it is rare that you’ll have to use the rules listed above. About the only time you’ll actually calculate probabilities by adding and multiplying is when figuring out the expected values for a goodness-of-fit test.
Probabilities In Genetics: Why Is It Important
Probability is a method for determining the likelihood of something uncertain occurring. If you flip a coin, you do not know whether it will be heads or tails, but probability can tell you that there is a 1/2 chance of either happening.
If a doctor wants to calculate the probability that a couples future offspring will inherit a disease found on a specific genetic locus such as cystic fibrosis, she can also use probabilities.
Consequently, professionals in the medical fields make great use of probabilities as do those in agriculture. Probability helps them with breeding of livestock, with weather predictions for farming and with crop yield predictions for the market.
Probabilities are also essential for actuaries: Their job is to calculate levels of risk for various populations of people for insurance companies so that they know the cost of insuring a 19-year-old male driver in Maine, for example.
TL DR
Probability is a method used to predict the likelihoods of uncertain outcomes. It is important for the field of genetics because it is used to reveal traits that are hidden in the genome by dominant alleles. Probability allows scientists and doctors to calculate the chance that offspring will inherit certain traits, including some genetic diseases like cystic fibrosis and Huntington’s disease.
Probability Definition In Math
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e. how likely they are to happen, using it. Probability can range in from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.
For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible . But if we toss two coins in the air, there could be three possibilities of events to occur, such as both the coins show heads or both show tails or one shows heads and one tail, i.e., ,.
Don’t Miss: What Does Denominator Mean In Math
When It Comes To Genetic Inheritance From Parent To Offspring There Isnt A Guaranteed Outcome But There Are Ways To Assess The Possible Outcomes
Genetic heredity is inherently probabilistic sexual reproduction ensures that even when we know everything about the parentsgenomes, we dont know what assortment of their genes will end up in each of their offspring. It can be fun to wonder if a new baby will look more like their mum or dad, but when a genetic condition runs in the family, the unpredictability can be worrying.
We can, however, predict the possible outcomes based on chance. For example, for a couple who are both carriers of the gene variant for a recessive condition, the chance that their child will be affected is 25%. But it does not follow that if they have three healthy children, then the fourth will have the condition. They could have four healthy children, or four who are all affected. The 1-in-4 chance is the same each time, for each child.
Mendel’s Experiments On Pea Plants
A nineteenth-century botanist named Gregor Mendel, and the namesake for Mendelian genetics, used little more than pea plants and mathematics to intuit the existence of genes and the basic mechanism of heredity, which is how traits are passed to offspring.
He observed that his pea plants observable traits, or phenotypes, did not always yield the expected ratios of phenotypes in their offspring crops. This led him to conduct crossbreeding experiments, observing the phenotype ratios of each generation of offspring plants.
Mendel realized that traits could sometimes be masked. He had made the discovery of the genotype and had set the field of genetics in motion.
Recommended Reading: Who Is Oersted In Physics
Garden Pea Characteristics Revealed The Basics Of Heredity
In his 1865 publication, Mendel reported the results of his crosses involving seven different characteristics, each with two contrasting traits. A trait is defined as a variation in the physical appearance of a heritable characteristic. The characteristics included plant height, seed texture, seed color, flower color, pea pod size, pea pod color, and flower position. For the characteristic of flower color, for example, the two contrasting traits were white versus violet. To fully examine each characteristic, Mendel generated large numbers of F1 and F2 plants, reporting results from 19,959 F2 plants alone. His findings were consistent.
What results did Mendel find in his crosses for flower color? First, Mendel confirmed that he had plants that bred true for white or violet flower color. Regardless of how many generations Mendel examined, all self-crossed offspring of parents with white flowers had white flowers, and all self-crossed offspring of parents with violet flowers had violet flowers. In addition, Mendel confirmed that, other than flower color, the pea plants were physically identical.
| The Results of Mendels Garden Pea Hybridizations |
|---|
| Characteristic |
When One Parent Is Homozygous:
When one parent is homozygous, the other parent is heterozygous. The Punnett square from one homozygous parent and one heterozygous parent is below.
When the parent is homozygous and has two dominant alleles, all the descendants will have the same dominant trait phenotype. To put it another way, there is a ten out of ten possibility that when a descendant has a pairing of that nature, this pairing will show the dominant phenotype. Now we can also study that there is a possibility that the homozygous parent has two recessive alleles. Now half of the descendants will show the recessive trait with genotype bb. The other half will show the dominant trait, with heterozygous genotype Bb.
Recommended Reading: What Does Dilation Mean In Math
Recessive And Dominant Traits And The Law Of Segregation
From Mendels experiments, he came up with several rules for understanding what must be happening to explain the pattern of trait inheritance in his pea plants. One of them was the law of segregation, which still explains heredity today.
For each trait, there are two alleles, which separate during the gamete formation phase of sexual reproduction. Each sex cell contains only one allele, unlike the rest of the bodys cells.
When one sex cell from each parent fuses to form the cell that will grow into the offspring, it has two versions of each gene, one from each parent. These versions are called alleles. Traits can be masked because there is often at least one allele for each gene that is dominant. When an individual organism has one dominant allele paired with a recessive allele, the individual’s phenotype will be that of the dominant trait.
The only way a recessive trait is ever expressed is when an individual has two copies of the recessive gene.
Mathematical Probability And Statistical Probability:
When the probability is calculated on the basis of reasoning even before any trial or experiment hat is called mathematical or apriori probability. In practice, the actual probability calculated by trials may not coincide with apriori probability, for example, when a coin is tossed one gets the head , though the mathematical probability of occurrence of head is only 1/2 in the trial P = 1 or P = O.
But if the coin is tossed 10 times, the occurrence of head can be O or 1 or 2 or 3 or 10, the extreme cases being very rare. Suppose H occurred 4 times out of 10 trials. Now consider the occurrence of H as the favourable event, the occurrence of H 4 times out of 10 trials gives the relative frequency 4/10 for H .
But if the number of tosses is increased, it is likely that the ratio of the occurrence of favourable event becomes more close to 1/2. In general, if favourable event, say head , occurs n time out of N trials, the relative frequency of favourable event will be n/N. The limit of this relative frequency as N becomes infinitely large is known as statistical probability.
Also Check: Are Quantum Physics And Spirituality Related
Additional Example: Improvement With Surgical Experience
An ophthalmologist investigated his learning curve in performing radial keratotomies9. He was able to perform a 1-month postoperative refraction on 78 of his first 100 eyes. He classified them as 20/20 or better versus worse than 20/20. The results appear in Table 9.5. The ophthalmologist notes that the percentage of eyes in the 20/20 or better group increased from 41% to 73% from earlier to later surgeries. The null hypothesis is that resultant visual acuity is independent of when in the sequence the surgery was done. FET yields p = 0.006. The ophthalmologist rejects the null hypothesis and concludes that his surgical skills have improved significantly.
Table 9.5. Refraction of Postoperative Eyes by Position in Sequence of Surgery
| No. Eyes in First 50 | No. Eyes in Second 50 | Totals |
|---|
R.H. Riffenburgh, in, 2012
What Is The Role Of Probability In Monohybrid Inheritance
Using Probability to Determine Alleles in Gametes In Mendels monohybrid cross, two heterozygous plants are crossed. Both plants produce gametes, all of which contain either a P or p allele for flower color. The likelihood that any particular gamete contains the allele for a white flower can be calculated.
Read Also: Geometry Dash Hexagon Force Scratch
Key Definitions Of Probability In Genetics
The sum law – To find the probability of two events occurring, as long as all the events are mutually exclusive , you must add the probabilities of each individual event occurring together.
The sum law is also known as the “OR” rule. If you see phrases containing the word “or”, you should use the sum law. For example, “what is the probability of this OR that occurring?” or “what is the probability of expressing this OR that trait?”.
The product law – To find the probability of two events occurring, as long as all the events are independent of one another , multiply the probabilities of all individual events occurring.
The product law is also known as the “AND” or “BOTH” rule. When you see phrases containing “and” or “both”, you should use the product law. For example, “What is the probability of this AND that occurring?” or “What is the probability of expressing BOTH traits?”.
What Are Equally Likely Events
When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:
- Getting 3 and 5 on throwing a die
- Getting an even number and an odd number on a die
- Getting 1, 2 or 3 on rolling a die
are equally likely events, since the probabilities of each event are equal.
You May Like: What Is The Molecular Geometry Of No2
Biology Review Of Genetics And Probability
Overview: Chance and ProbabilityGeneticists use the principles of chance and probability to express the results of genetic experiments with pea plants, as well as other plants and animals. In mathematical terms, probability refers to the fraction of times an event can occur. According to the product rule for independent events. the probability of events occurring together is the product of the probabilities for each event multiplied. For example, the probability of a girl being born is 50 % , but the probability for two girls being born in the same family is 50% x 50% =25%. This does not necessarily mean that a specific family will have a girl if another family has a boy at the same time, just that the overall probability, in a sample of many, will be 50%.
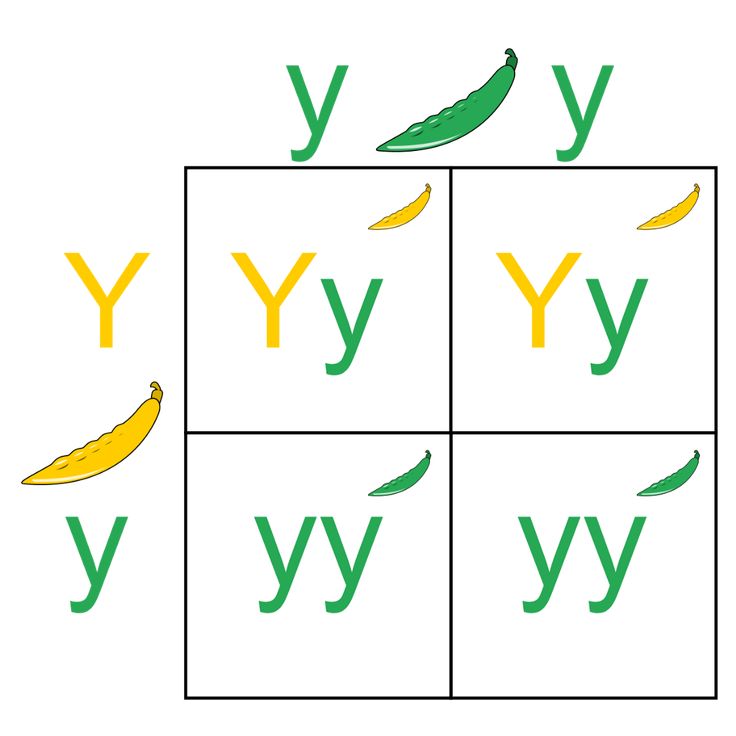
Punnett Squares and TestcrossesThe range of probable genetic crosses can be demonstrated by drawing a simple grid with all the alleles contributed by one parent on one side and the other parent on the other, then showing each possibility in each square of the grid. That way, all the possibilities can be accounted for.
Interested in Science tutoring services? Learn more about how we are assisting thousands of students each academic year.
Using Probability Vs Punnett Squares
Mendel used probability mathematics to calculate the outcomes of each generation of pea plants, but sometimes a visual representation, such as the Punnett square, can be more useful.
A trait is homozygous when both alleles are the same, such as a blue-eyed person with two recessive alleles. A trait is heterozygous when the alleles are not the same. Often, but not always, this means that one is dominant and masks the other.
A Punnett square is particularly useful for creating a visual representation of heterozygous crosses even when an individuals phenotype masks the recessive alleles, the genotype reveals itself in Punnett squares.
The Punnett square is most useful for simple genetic calculations, but once you are working with a large number of genes influencing a single trait or looking at overall trends in large populations, probability is a better technique to use than Punnett squares.
Related Articles
Don’t Miss: What Is Eq In Psychology
Using Probabilities To Calculate Possible Outcomes
Using probabilities allows scientists to predict the outcome for specific traits, as well as to determine the potential genotypes of offspring in a specific population. Two kinds of probability are especially relevant to the field of genetics:
- Empirical probability
- Theoretical probability
Empirical, or statistical probability, is determined with the use of observed data, such as facts collected during in a study.
If you wanted to know the probability that a high school biology teacher would call on a student whose name started with the letter J to answer the first question of the day, you might base it on observations you had made over the past four weeks.
If you had noted the first initial of each student whom the teacher had called on after asking his first question of the class on every school day in the past four weeks, then you would have empirical data with which to calculate the probability that the teacher would first call on a student whose name begins with a J in the next class.
Over the past twenty school days, the hypothetical teacher called on students with the following first initials:
The data shows that the teacher called on students with a first initial J four times out of a possible twenty times. To determine the empirical probability that the teacher will call on a student with a J initial to answer the first question of the next class, you would use the following formula, where A represents the event for which you are calculating the probability:
The Punnett Square Approach For A Monohybrid Cross
Read Also: What Does C Stand For In Physics
What Is Probability
Probability denotes the possibility of the outcome of any random event. The meaning of this term is to check the extent to which any event is likely to happen. For example, when we flip a coin in the air, what is the possibility of getting a head? The answer to this question is based on the number of possible outcomes. Here the possibility is either head or tail will be the outcome. So, the probability of a head to come as a result is 1/2.
The probability is the measure of the likelihood of an event to happen. It measures the certainty of the event. The formula for probability is given by
P = Number of Favourable Outcomes/Number of total outcomes
P = n/n
n = Number of event favourable to event E
n = Total number of outcomes
Why Do We Use Ranks
Statistical methods using continuous measurements on variables depend on the probability distributions of those variables. We assume certain properties of those probability distributions, such as that we are sampling from a normal distribution. We may have evidence that the assumptions are not satisfied. Recall that the distribution of prostate volumes is skewed to the right. Using methods that assume a normal distribution would violate this assumption, because the sample distribution is not the same shape as the assumed distribution, causing the probability calculations to be wrong. Rank-order methods, not subject to the skew, would not violate the assumption. Furthermore, when we have small sample sizes, our sample frequency distributions are insufficient to tell us if the assumptions are justified. Rank-order methods do not require as stringent assumptions about the underlying distributions.
Also Check: How To Support Ell Students In Math