Kinematic Equations In Physics
The kinematics equations, also known as equations of motion, are a set of four key formulas we can use to find the position, velocity, acceleration, or time elapsed for the motion of an object. Lets walk through each of the four kinematic equations and how to use them.
The first kinematic equation allows us to solve for the final velocity given an initial velocity, acceleration, and time period:
\begin v=v_0+a \Delta t \end
where \ is the initial velocity, \ is the acceleration, and \ is the time elapsed. The next kinematic equation lets us find the position of an object given its initial position, initial and final velocities, and elapsed time:
\begin x=x_0+ \Delta t,\, \mathrm \\ \Delta x= \Delta t \end
where \ is the initial position in the \-direction. We can substitute \ for \ or \ for motion in any other direction. Notice how weve written this equation in two different ways since the displacement \ is equal to \, we can move our initial position variable to the left side of the equation and rewrite the left side as the displacement variable. This handy trick also applies to our third kinematic equation, the equation for the position given the initial position, initial velocity, acceleration, and elapsed time:
\begin x=x_0+v_0t+\fraca\Delta t^2,\, \mathrm \\ \Delta x=v_0t+\fraca\Delta t^2 \end
\begin v^2=v_0^2+2a\Delta x \end
What Have You Learned In Kinematics
To describe motion, kinematics studies the trajectories of points, lines and other geometric objects. The study of kinematics can be abstracted into purely mathematical expressions. Kinematic equations can be used to calculate various aspects of motion such as velocity, acceleration, displacement, and time.
Linear Motion In One Dimension
What are the given values?$ \large v_0 = 5 \textrm $$ \large v_0 = 0 \textrm $$ \large x – x_0 = 23 \textrm m $
We can rearrange the second kinematics formula $ \Delta x = t $
Substitute our equation for $ \Delta x $ and rearrange the equation. $ x – x_0 = \frac t $
Arrange the equation to solve for $ \large t $, and plug in our known values to solve.
$ \Large t = 2 = 2 = \large 11.6 \textrm s $
You May Like: What Is Mass Number In Chemistry
Absolute Scale Of Neutrino Mass
Direct kinematic methods measurements of the Curie plot of the 3H decay near the end point give me< 2.05 eV , Troitsk after anomaly subtraction . And the updated in 2004 result from Mainz experiment me< 2.3 eV . Future KATRIN experiment aims at one order of magnitude better upper bound: me< 0.2 eV . The discovery potential is estimated so that the positive result me = 0.35 eV can be established at 5 level.
From oscillation experiments we get the lower bound on mass of the heaviest neutrino:
Christoph Grab, representing the H1 and ZEUS collaborations, in, 2003
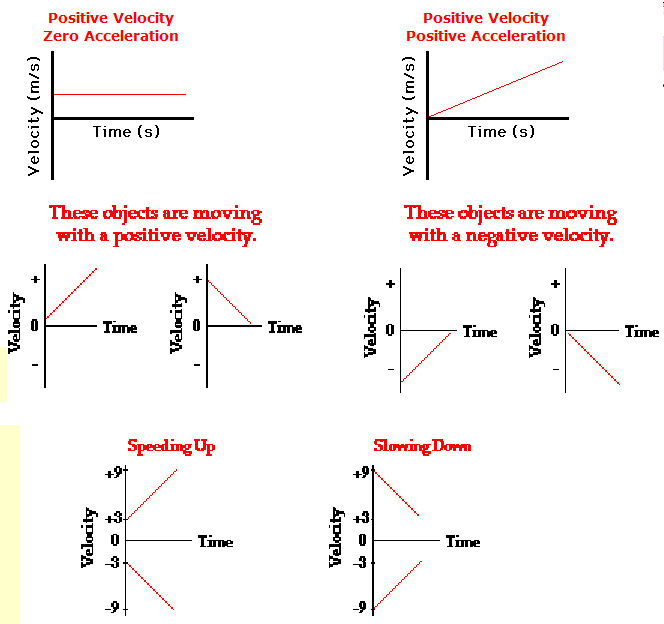
Speed And Velocity In Kinematics
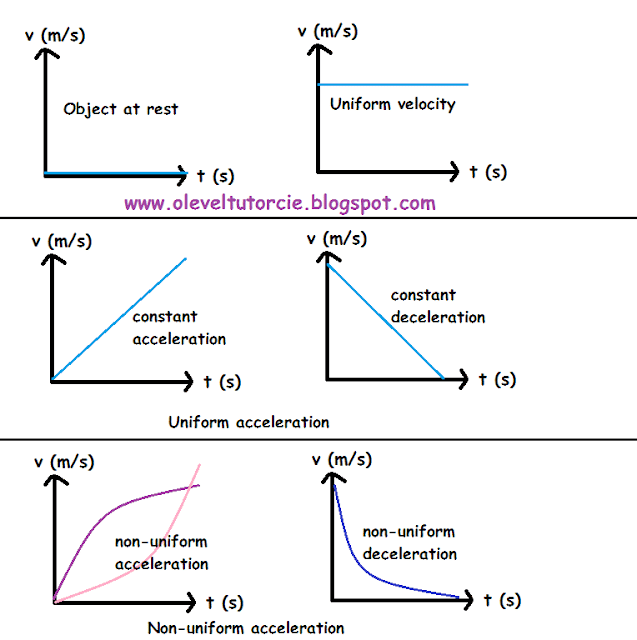
When studying the motion of objects, we may need to know more than just where they went we may also need to know how quickly they got there. For this, we can refer to speed and velocity. These terms may both be rather familiar, but they have very specific uses in physics. There are also some key differences between speed and velocity that you will see below.
Don’t Miss: What Is Natural Selection In Biology
How Kinetics Is Different From Kinematics
Kinetics is the study of forces that cause motion while kinematics is a mathematical description of motion that doesn’t refer to forces. … Kinematics doesn’t regard the mass of any object in the system to describe its motion, whereas kinetics does. Kinematics can be considered a branch of mathematics.
Kinematics Of A Particle Trajectory In A Non
mrvarva
Particle kinematics is the study of the trajectory of particles. The position of a particle is defined as the coordinate vector from the origin of a coordinate frame to the particle. For example, consider a tower 50 m south from your home, where the coordinate frame is centered at your home, such that east is in the direction of the x-axis and north is in the direction of the y-axis, then the coordinate vector to the base of the tower is r = . If the tower is 50 m high, and this height is measured along the z-axis, then the coordinate vector to the top of the tower is r = .
In the most general case, a three-dimensional coordinate system is used to define the position of a particle. However, if the particle is constrained to move within a plane, a two-dimensional coordinate system is sufficient. All observations in physics are incomplete without being described with respect to a reference frame.
The position vector of a particle is a vector drawn from the origin of the reference frame to the particle. It expresses both the distance of the point from the origin and its direction from the origin. In three dimensions, the position vector r
The trajectory of a particle is a vector function of time, r , which defines the curve traced by the moving particle, given by
Also Check: How To Impress Your Physics Teacher
How To Prepare Kinematics
Before solving questions you should have a good command over basic calculus, you should be able to differentiate and integrate functions. For getting a good hold on the concepts you should first solve the question from one-dimensional motion then only solve the 2-dimensional motion. Also, learn the basics of making graphs. After reading a topic take a few mock tests on that particular topic to get the strength on the topic. Sometimes questions asked from relative motion, projectile motion and river problem are difficult hence practice more on these topics.
Example : Distance And Displacement Going To School
Assume the image above shows the arrangement of your home, school, and favorite bakery. If a morning walk to school involves stopping at the bakery for a breakfast pastry, find your distance and displacement for the trip.
How to Find Distance
To find the distance you will need to account for the length of the entire trip from the home, past the school, to the bakery, and then back to the school. In this case:
\text=60\text+30\text+30\text
\text=120\text
How to Find Displacement
To find the displacement you only need to look at how far apart the starting and ending points are. In this case, you started at home and ended at school. These two locations are 60\text apart so:
\text=60\text
Also Check: What Does Causation Mean In Math
Etymology Of The Term
The term kinematic is the English version of A.M. Ampère‘s cinématique, which he constructed from the Greekκίνημαkinema , itself derived from κινεá¿Î½kinein .
Kinematic and cinématique are related to the French word cinéma, but neither are directly derived from it. However, they do share a root word in common, as cinéma came from the shortened form of cinématographe, “motion picture projector and camera”, once again from the Greek word for movement and from the Greek γÏá¾°ÌÏÏgrapho .
What Are Kinematics Examples
In other words, kinematics describes the way motion is happening. But, it doesn’t take into account the cause of the motion of the body. Some important parameters in kinematics are displacement, velocity, time, etc. Some popular examples of motion are vertical motion, horizontal motion, and projectile motion.
Read Also: What Is Ligand In Chemistry
Kinematic Formula For Velocity
Velocity has a somewhat similar definition, but instead of being the rate of change of distance, it is the rate of change of displacement. Velocity measures how quickly an object changed its position, regardless of how long the path was. Because velocity is based upon displacement, a vector quantity, velocity is also a vector quantity with both a magnitude and a direction. Velocity is represented by a v in equations and is equal to the displacement divided by the change in time.
| Formula for Velocityv=\Delta x/\Delta t |
Here again, \Delta t is the change in time. Similar to speed, velocity units can be derived from the equation. Displacement is measured in meters while time is measured in seconds so meters divided by seconds give us meters per second .
Note: Depending on the level of physics course you are taking and what textbook your course is referencing, you may only see t to represent time rather than \Delta t.
The Program Of Particle Kinematics
Kinematics is the branch of mechanics that deals with the description of motion. It does not deal with the causes of motion. In the first four sections of this chapter we introduced the variables required to describe the motion, and the changes in the motion, of a particle. When we set up definitions of velocity and acceleration we started with position and time, and then deduced the velocity and the acceleration. It is useful to pause at this point to ask the question What is the purpose of kinematics? We will see that the answer To obtain future values of position and velocity of a system in terms of its present values of position and velocity and its accelerations exactly reverses the order of the logic just outlined.
Consider the defining equation of average velocity.
reveals the final velocity, vf, at the time tf, providing the initial velocity, vi, initial time, ti, and average acceleration during the time interval t are known. Thus the average acceleration, if known, may be thought of as a quantity that provides future values of velocity.
Kinematics starts with the acceleration of a particle and uses this acceleration to predict the future positions and velocities of the particle. But how do we determine the acceleration of a particle? The dynamic laws of nature contain the answer to this question. In Chapter 6 we will see how the acceleration of a particle is related to the external forces acting on the particle through Newton’s
Frank Fahy, in, 2001
Recommended Reading: How To Add Compounds Chemistry
Dynamics Cart And Track System
are multi-purpose equipment sets that enable educators to demonstrate and teach a variety of complex physics topics in Kinematics and Dynamics.Since their invention, PASCOs dynamics systems have become essential tools in physics labs around the world.Our dynamics systems are complete experiment solutions that enable students to observe, measure and analyze motion through hands-on experimentation.Whether youre new to dynamics systems, or youre looking to enhance your current systems capabilities, we offer a range of customizable dynamics systems to fit your budget and needs.
List the known values.$ \large v_0 = 0 \textrm $$ \large v = 13 \textrm $$ \large x – x_0 = 150 \textrm m $
Start with the first kinematics formula $ \large v^2 = ^2 \normalsize + 2a \Delta x $ and plug $ \large x – x_0 $ in for $ \Delta x $.
$ \Large v^2 = ^2 + 2a $
Rearrange the equation to solve for acceleration and plug in our known values, then solve.
$ \Large a = \frac ^2} = \frac )^2 – ^2} = \large }^2 $
Kinetics In Everyday Life
Kinetics and kinetic energy can be seen and experienced in our everyday lives as well. Certain examples are-
-
It can be seen in hydropower plants, in here due to the kinetic energy of the water the plants can generate electricity.
-
Generation of electricity with the help of windmills which are in motion.
-
Moving cars possess kinetic energy.
-
The motion of a bullet since force is applied via the gun possesses kinetic energy.
-
Cycling as we apply force for the movement of pedals. Pedalling scents the bicycle in kinetic motion.
Also Check: How To Increase Torque Physics
Is Displacement A Vector A Scalar Quantity
There is another key difference between distance and displacement one is a vector and one is a scalar. Because distance accounts for the entire path taken, choosing a direction is not entirely possible. If you consider our race track above, you would have to include different directions for every turn and straightaway. Instead, we only take into account the magnitude of distance traveled, making it a scalar quantity.
Conversely, displacement looks only at starting and ending points. These will have a set distance between them in one direction from a given frame of reference. Because magnitude and direction are both important, displacement is considered a vector quantity.
Point Trajectories In A Body Moving In The Plane
The movement of components of a mechanical system are analyzed by attaching a reference frame to each part and determining how the various reference frames move relative to each other. If the structural stiffness of the parts are sufficient, then their deformation can be neglected and rigid transformations can be used to define this relative movement. This reduces the description of the motion of the various parts of a complicated mechanical system to a problem of describing the geometry of each part and geometric association of each part relative to other parts.
Geometry is the study of the properties of figures that remain the same while the space is transformed in various waysâmore technically, it is the study of invariants under a set of transformations. These transformations can cause the displacement of the triangle in the plane, while leaving the vertex angle and the distances between vertices unchanged. Kinematics is often described as applied geometry, where the movement of a mechanical system is described using the rigid transformations of Euclidean geometry.
The coordinates of points in a plane are two-dimensional vectors in R2 . Rigid transformations are those that preserve the distance between any two points. The set of rigid transformations in an n-dimensional space is called the special Euclidean group on Rn, and denoted SE.
Don’t Miss: Chapter 6 Mid Chapter Test Glencoe Algebra 2
Iaatomic Collisions In The Kiloelectron
The kinematics of atomic collisions in the kiloelectron-volt range is accurately described through classical mechanics by considering the mutual Coulomb repulsion between the colliding atomic cores. The scattered primary atom loses some of its energy to the target atom which, in turn, is recoiled into a forward direction. The energies of the scattered and recoiled atoms and the directions of their trajectories are determined by the masses of the colliding pair and the closeness of the collision.
By applying the laws of conservation of energy and momentum, the TOF of an incident ion of mass M1 and energy E0 which is scattered from a target atom of mass M2 into an angle is given by
t ) for all × SM. For a proof of Liouville’s theorem, compare A. Besse .
We recall some notations and facts from our discussion of geodesic polar coordinates in Section III.1. For a fixed p M, the function c = c, Sp is the distance to the cut point of p along , that is, t = d) for all t is known to be continuous, and inj
James Proudfoot, in, 2003
Introduction To Scalars And Vectors
A vector is any quantity that has both magnitude and direction, whereas a scalar has only magnitude.
learning objectives
- Distinguish the difference between scalars and vectors
What is the difference between distance and displacement? Whereas displacement is defined by both direction and magnitude, distance is defined by magnitude alone. Displacement is an example of a vector quantity. Distance is an example of a scalar quantity. A vector is any quantity with both magnitude and direction. Other examples of vectors include a velocity of 90 km/h east and a force of 500 newtons straight down.
Scalars and Vectors: Mr. Andersen explains the differences between scalar and vectors quantities. He also uses a demonstration to show the importance of vectors and vector addition.
In mathematics, physics, and engineering, a vector is a geometric object that has a magnitude and direction and can be added to other vectors according to vector algebra. The direction of a vector in one-dimensional motion is given simply by a plus or minus sign. A vector is frequently represented by a line segment with a definite direction, or graphically as an arrow, connecting an initial point A with a terminal point B, as shown in.
Vector representation: A vector is frequently represented by a line segment with a definite direction, or graphically as an arrow, connecting an initial point A with a terminal point B.
Scalars vs. Vectors: A brief list of quantities that are either scalars or vectors.
Recommended Reading: What Are The Biological Causes Of Depression
Kinematic Formula For Distance
To find the distance and displacement of different movements, we have two equations to use. For distance, we add up the distances of each segment of a motion. Distance is typically measured in meters and represented in equations by the symbol d.
| Formula for Distanced_=d_+d_+…+d_ |
Here, d_ is the total distance traveled, and d_ and d_ are the first and second segments, respectively. In some problems, you may have only one or two distances to add together while in others you may have more. d_ represents the highest number segment you have to add. If you go back to our race track, there were 10 loops. That means we had 10 segments so, d_ would be d_.
Kinematic Formula For Displacement
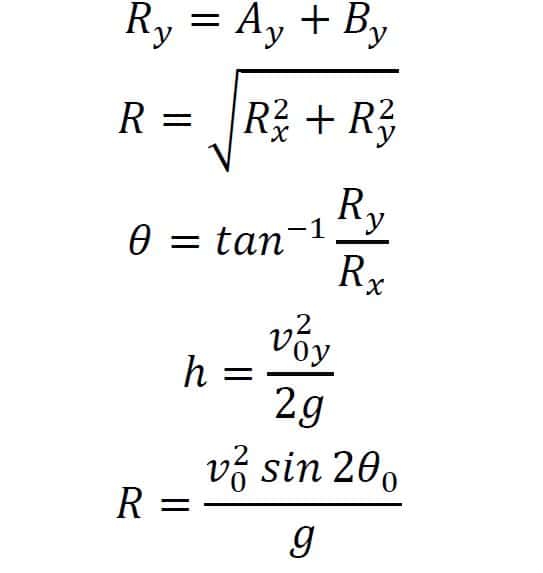
Displacement is still measured in meters, but it is represented by \Delta x. The \Delta symbol is called a delta and can be thought of as meaning change in. In the case of displacement, \Delta x means change in position.
| Formula for Displacement\Delta x=x_-x_ |
Here, \Delta x is the net displacement , x_ is the final position, and x_ is the initial position. It is important to note that if your initial position has a higher value than your final position, your displacement can be negative.
Depending on the level of physics course you are taking and what textbook your course is referencing, you may see only x or x_ to represent overall or total displacement.
Recommended Reading: What Does Cohesion Mean In Biology
Defining A Frame Of Reference
A frame of reference is another important concept when talking about studying the motion of objects. When we talk about a frame of reference, we are talking about what an observer would see from a given position. Consider the van driving down the coast in the image. An observer standing on the left-hand side of the photo by the sign would see the van moving away. Meanwhile, an observer standing on the opposite side would see the van approaching. Being able to utilize a frame of reference allows us to better collect and share accurate data especially when working with other scientists.