How Can I Learn Geometry Easily
The best way to truly master geometry painlessly isnt rote memorization: its looking at principles in practice.
It can be tempting to sit down with a basic list of geometry formulas, memorize them, and brush off your hands. However, to really master geometry, its not just about learning the formulasits about putting them into practice.
With that said, the easiest way to learn geometry is to see how formulas apply to a wide variety of question types. The key to this is to use high-quality materials to do a lot of geometry questions, then reading the answers and explanations after youve answered themeven if youve answered them correctly!
Why would you want to read question explanations if youve answered a question correctly? Because there may be a way to answer the question more quickly and efficiently than you didand yes, this includes the use of geometry formulas!
P.S. If youre looking for a shortcut for solving geometry equations, click here!
Solved Examples Using Geometry Formulas
Example 1: Calculate the circumference and the area and of a circle by using geometry formulas if the radius of the circle is 21 units?
Solution:
To find the area and the circumference of the circle:
Given: Radius of a circle = 21 unitsUsing geometry formulas for circle,Area of circle = ×r2 = 3.142857 × 212Now for the circumference of the circle,Using geometry formulas for circle,Circumference of a Circle = 2r= 2= 131.95
Answer: The area of a circle is 1385.44 sq. units and the circumference of a circle is 131.95 units.
Example 2: What is the area of a rectangular park whose length and breadth are 60m and 90m respectively?
Solution:To find the area of a rectangular park:
Given: Length of the park = 60m
The breadth of the park = 90mUsing geometry formulas for rectangle,
Area of Rectangle =
= m2
= 5400 m2
Answer: The area of the rectangular park is 5400 m2.
Example 3: Using geometry formulas of the cube, calculate the surface area and volume of a cube whose edge is 6 units respectively?
Solution:To Find: The surface area and volume of a cube whose edge is 6 units
Using geometry formulas of cube,Surface area of cube is = A = 6a2A = 6 2A = 6 × 36 = 216 units2Volume of a cube, V = a3V = 3V = 216 units3
Answer: The surface area of the cube is 216 units2. The volume of the cube is 216 units3
List Of Math Area Formulas
The surface Area of a plane covers the plane from side to side on a two dimensional surface. Remember to convert measurements to the same units of measurement. Measurements in one kind of unit give give the answer as that unit squared since unit x unit = u2 u*u=u2 Inches x inches = inches2 in x in = in2
These are the basic geometry formulas for Area:
- Square Area length of side x length of side = Area of a Square s*s=A s2
- Rectangle Area length x width = Area lw=A
- Parallelogram Area base x height = Area bh=A
- Trapezoid Area h/2(b1 + b2
- Circle Area pir2 = Area of a Circle
- Elipse Area pir1r2 = Area of an Elipse
- Triangle Area half of base x height = Area of a Triangle bh/2=A
- Equilateral Triangle Area square root of 3 divided by 4 x side squared = Area of an Equilateral Triangle 3/4
Our printable multiplication and worksheets are a first step in learning regular sided perimeter, area, and volume formulas. Find our multiplication worksheets here.
Maria Miller’s Math Mammoth area workbook is very helpful and you can get it at .
Also Check: What Happened To The Computer Programmer Algebra With Pizzazz
Geometry Formulas: Special Parallelograms
There are three categories of special parallelograms: rhombuses, rectangles, and squares. The BIG FOUR parallelogram properties above apply to all of them.
A rhombus is an equilateral quadrilateral, that is, a quadrilateral with four equal sides.
Most diamond shapes, such as those on playing cards, are simply rhombuses turned sideways, like the one on the right above. If the side is s, then the perimeter is always just 4s. The diagonals of a rhombus are always perpendicular. In fact, any rhombus can be subdivided into four congruent right triangles.
As with a general parallelogram, A = bh, where the b is any side and the h is the length of a perpendicular segment: as with a general parallelogram, the Pythagorean Theorem may play a role in finding one of the lengths that you need.
A rectangle is an equiangular quadrilateral, that is, a quadrilateral with four 90° angles.
Each angle is 90° and the two diagonals are always equal in length: its an old carpenters trick to verify that a doorframe has four right angles simply by checking the lengths of the two diagonals. Of course, its usually easy to find the length of a diagonal using the Pythagorean theorem.
The area of a rectangle is simply A =bh, where the base & height are simply lengths of any two adjacent sides. The perimeter is P = 2b + 2h.
\\ \
Geometry Formulas: Higher Polygons
A polygon is any closed figure with three or more line-segment sides. We have already discussed triangles and quadrilaterals. Here is a handy chart for the names:
| Number of sides |
|---|
| 10 |
For any n-sided polygon, the sum of all the angles in the polygon is given by sum = . Any triangle has a sum of 180°, any quadrilateral has a sum of 360°, any pentagon has a sum of 540°, etc.
Another important idea is the idea of a regular polygon. This is a particularly tricky word: in ordinary speech, regular means ordinary, commonplace. In geometry, it has almost the opposite meaning. The regular polygons are the most elite and symmetrical shapes. A regular polygon is one that has all equal sides and all equal angles. The regular triangle is the equilateral triangle, and the regular quadrilateral is the square. In a regular polygon, because we can compute the sum of the angles, we can divide this by the number of angles to get the individual angle measure.
The regular octagon, of course, is the stop signshape in many countries around the world.
As we saw above, quadrilaterals have two diagonals. Pentagons have five, and higher polygons have many more. See this post about the diagonals of a regular octagon. The diagonals of the regular pentagon trace out the standard five-pointed star, such as the stars on the flag of the United States of America.
You May Like: What Is Configuration In Chemistry
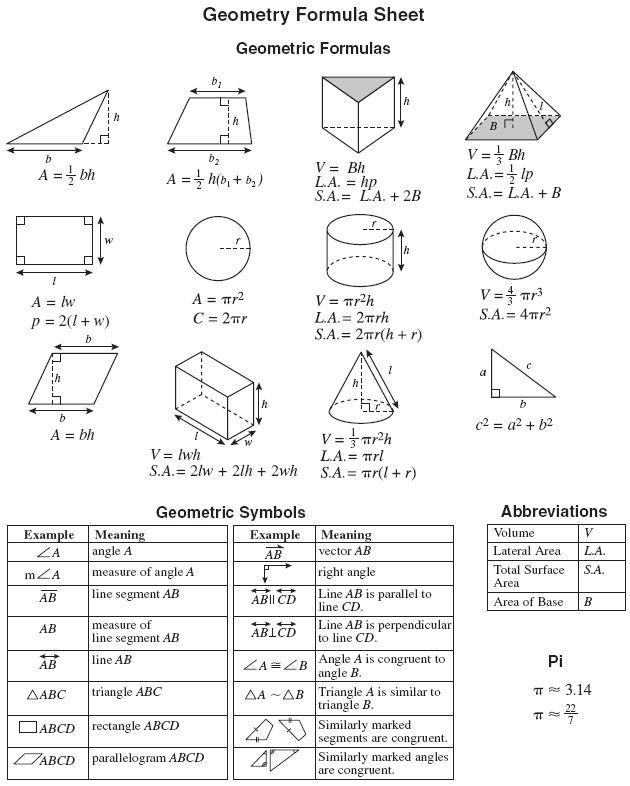
List Of Geometry Formulas
- Area of a Trapezoid = ½× \\) × height
Basic geometry formulas where the mathematical constant is used are,
The formula table depicts the geometry formulas used for different 2-D and 3-D shapes:
| SHAPES | |
|
Pythagoras Theorem: a2 + b2 = c2 Area = ½ ab Perimeter = a + b + Where,c = hypotenuse of a triangle a = altitude of a triangle b = base of a triangle |
|
| 2. Triangle |
Perimeter, P = a + b + c Area, A = ½ bh |
|
l = length of a rectangle w = width of a rectangle |
|
|
a and b are the sides of a parallelogram h = height of a parallelogram |
|
|
a and b are the parallel sides h = distance between two parallel sides |
|
| 6. Circle |
r = radius of a circle |
| 7. Square |
Side, a = A = d/22 Where, a = side of a square |
| 8. Arc |
Here, is the central angle is radians. Where, |
|
a = side of a cube |
|
| 10. Cuboid |
Surface Area, A = 2 Volume, V = lbh Space diagonal, d = Where, |
|
Total Surface Area, A = 2rh + 2r2 Curved Surface Area, Ac = 2rh Volume, V = r2h r= radius of a cylinder h= height of a cylinder |
|
| 12. Cone |
Total Surface Area, A = r = r Curved Surface Area, Ac = rl Volume, V = r2h Slant Height, l = Base Area, Ab = r2 r= radius of a cone h= height of a cone l = slant height |
|
r= radius of a sphere |
Let’s have a look at solved examples to understand geometry Formulas better.
Geometry Rules: All Triangles
A triangle is a shape with three line segment sides.
Facts about all triangles:
In any triangle, the sum of the three angles is 180°.
Thats a big idea that Mr. Euclid , the great geometer, first proved. Heres another important geometry equation:
Theres more to that simple formula than means the eye. The letter b stands for the base: whats the base of a triangle? Naïvely, folks will say the bottom, the horizontal side, is the base, but thats not the whole story. In fact, any of the three sides can be the base. Similarly, the letter h is height: by height, we mean the length of a segment known as an altitude. An altitude is a line that passes through a vertex and is perpendicular to the side we are considering the base. Thus, for any triangle, we potentially have three different b & h combinations that would allow us to calculate the area.
Now, of course, the GRE is unlikely to give you all that information, three side lengths and three altitudes, in the course of a geometry problem. If a GRE geometry question ask for the area of the triangle, it will provide a way to find at least one base and the corresponding height. Keep in mind that the altitude divides the triangle into two little right triangles, so the Pythagorean Theorem may be involved in finding some of the necessary lengths.
The largest side is always opposite the largest angle, and the smallest side is always opposite the smallest angle.
Recommended Reading: What Is Succession In Biology
Geometry Rules: Right Triangles
Any right triangle has two sides touching the right angle: these are called legs. The longest side, always opposite the right angle, is called the hypotenuse.
One geometry rule that applies to all right triangles is theorem named for Mr. Pythagoras , whom some scholars consider the first mathematician.
Notice that the side we call c, the side alone on one side of the equation, has to be the hypotenuse. Also, notice that we can apply this formula unless we know a triangle is a right triangle, and that is not something we can assume simply from looks. If we get the litter perpendicular square, as we have here, then we know its a right triangle and we can apply this geometry equation.
Of course, some or all of the sides of a right triangle can be decimals, but it is possible, in special cases, for all three sides to be integers. These are sets of three integers that satisfy the Pythagorean Theorem. The most common is and its multiples, but other good ones to recognize are , , and .
There are two very special triangles that you have to understand for GRE geometry. The first is the 30-60-90 triangle:
We can multiply these lengths by any multiple, but they are always in this ratio. The short side, opposite the 30° angle, is always half the hypotenuse. The longer leg is always the square root of 3 times longer than the shorter leg. The ratios and angles in this triangle come direction from an equilateral triangle that was cut in half.
Geometry Formulas: Coordinate Geometry
A line in the coordinate plane can be represented in a few ways: the most common is slope-intercept form:
y = mx + b
The b is the y-intercept, the place where the line intersects the y-axis. The m is the slope. Slope is an indication of how tilted a line is. The slope of a horizontal line is zero. A vertical line has infinite slope. A 45° line has a slope of m = 1. To find the slope between two points A & B, draw a slope triangle:
If you do even a rough sketch, you should be able to read the rise and run off the graph, and then slope is just rise over run. Keep in mind, there are a few ways to think about any slope.
A slope of m = +3 means any of the following: to the right one unit, up 3 units
any multiple of
to the left one unit, down 3 units
any multiple of
A slope of m = 5/3 means any of the following:
to the right 1 unit, down 5/3 of a unit
to the right 3 units, down 5 units
any multiple of
to the left 1 unit, up 5/3 of a unit
to the left 3 units, up 5 units
any multiple of
The geometry rules concerning slope are very important to remember.
To find the y-intercept, set x equal to 0 and solve for y.
To find the x-intercept, set y equal to 0 and solve for x.
Parallel lines have equal slopes. Perpendicular lines have slopes that are opposite-signed reciprocals: for example, if the slope of one line is 3, the slope of the perpendicular line is + 1/3 if the slope of one line is +4/7, the slope of the perpendicular line is 7/4.
Recommended Reading: What Is Positive Reinforcement In Psychology
How Important Is Geometry In The Gre As A Whole
Two-dimensional geometry appears in approximately 15% of GRE Quant questions, while coordinate geometry accounts for around 4.4% of the section and three-dimensional geometry rounds this off, comprising 2.2% of questions. Overall, geometry questions account for around 21.6% of your GRE Math score, or about 1 in 5 questions.
For more on where geometry sits in the big picture of GRE Quant, and what other Quant concepts you should study, check out our post What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency.
Sample Gre Geometry Formula Practice Questions
Those are it in a nutshellthe GRE geometry formulas youll need on test day! However, memorizing formulas and putting them into practice are two very different things.
So that you can see the difference, weve pulled two problems from the Magoosh GRE prep course so you can try your hand at them.
Question 1: Multiple Choice1. The hypotenuse of a right triangle is 16 ft longer than the length of the shorter leg. If the area of this triangle is exactly 120 ft2, what is the length of the hypotenuse in feet?
A. 26
Check your answer and view the video explanation here!
Question 2: Numeric Entry2. In the diagram, point D is the center of the medium-sized circle that passes through C and E, and it is also the center of the largest circle that passes through A and G. Each of the diameters of the small circles with centers B and F equals the radius of the medium-sized circle with center D. The shaded area is what fraction of the largest circle?
Don’t Miss: What Does Fg Mean In Physics
Gre Geometry Equations & Formulas Are Good But
Finally, a word of caution. Knowledge of a formula, by itself, does not equal mathematical understanding. The GRE Quant doesnt care about your memorization of formulas: instead, it designs problems specifically to probe your understanding. Yes, its important to be conversant in the formulas, but knowledge of these formulas is less than 10% of what you need to understand on the GRE Quant. For more on this, see this GMAT blog: even if you skip the three hard practice problems at the beginning, the rest of the discussion is quite pertinent to the GRE Quant as well as the GMAT.
What Are Geometry Formulas
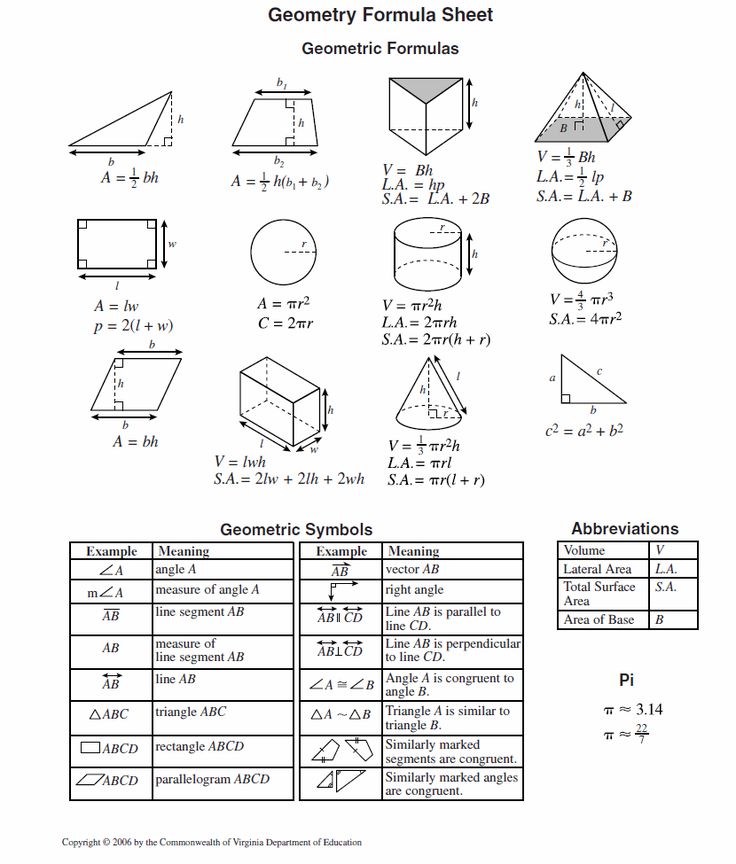
The formulas used for finding dimensions, perimeter, area, surface area, volume, etc. of 2D and 3D geometric shapes are known as geometry formulas. 2D shapes consist of flat shapes like squares, circles, and triangles, etc., and cube, cuboid, sphere, cylinder, cone, etc are some examples of 3D shapes. The basic geometry formulas are given as:
Also Check: What Does The Backwards E Mean In Math
Th Grade Math Reference Sheet
Math compound aids shapes perimeter worksheets area geometry subtracting adding regions worksheet grade shape composite figures algebra volume 5th mathematics. Fabulous in fifth!: mathematical mondays: math reference sheets. Vdoe whro pssa
Staar Formula Chart Algebra 1 – Math Formulas. 9 Pictures about Staar Formula Chart Algebra 1 – Math Formulas : Fabulous in Fifth!: Mathematical Mondays: Math Reference Sheets, Long Division Worksheets for 5th Grade and also Long Division Worksheets for 5th Grade.
What Are The Formulas In Geometry
Put very simply, geometry formulas are basic principles you can use to solve questions.
Of course , its not quite as simple as just plugging numbers blindly into a formula. The key to using geometry formulas is knowing when to use them: what kinds of questions they apply to and where to find the key numbers in the questions themselves.
The best way to master GRE geometry formulas? Practice, practice, practice!
You May Like: What Is Gene Expression In Biology
Geometry Rules: Angles And Lines
A right angle is made up of 90 degrees. A straight line is made up of 180 degrees.
In this diagram, ADC is a straight line. BTW, make sure you dont confuse straight lines with horizontal lines. Any line that doesnt bend or curve is straight, regardless of direction. By contrast, a horizontal line is parallel to the top or bottom of the page, parallel to the distant horizon. Line ADC is straight but not horizontal.
Notice, also, that straightness is one of the very few things we can assume on the GRE. If it looks like theres no bend in the line, then theres no bend: i.e. if it looks straight, it is straight. By contrast, we cannot assume perpendicularity: if we didnt have that special little blue square guaranteeing that the lines were perpendicular, we could not assume that either angle ADB or angle BCD were right angles. That is something we must be told, in one form or another.
If two lines intersect, the sum of the resulting four angles equals 360°. Furthermore, the angles opposite each other have to be equal. These angles meet at just a vertex, so they are called vertical angles .
When a line intersects a set of parallel lines, we get many more angles. We get eight angles: four big angles and four small angles. There are a number of technical names that we dont have to know for GRE geometry. We just have to know that every big angle is equal, every small angle is equal, and any big angle and any small angle are supplementary.