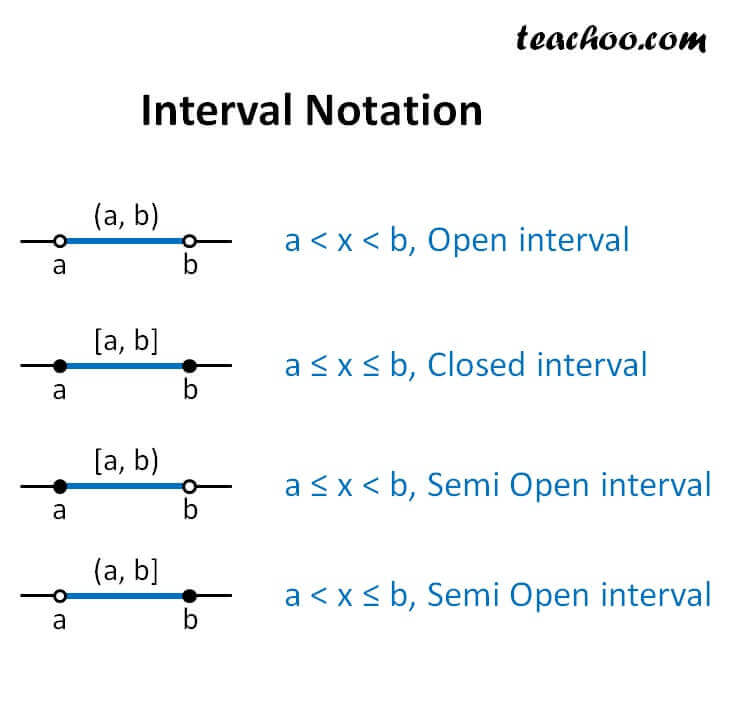
How To Convert Inequality To Interval Notation
We can convert inequality to interval notation using the below-given steps,
- Firstly, we need to graph the solution set of the interval on a number line.
- Then write the numbers in the interval notation with a smaller number appearing first on the number line on the left.
- Use the symbol “-” for the unbounded set on left and if it is unbounded on right, use the symbol “”.
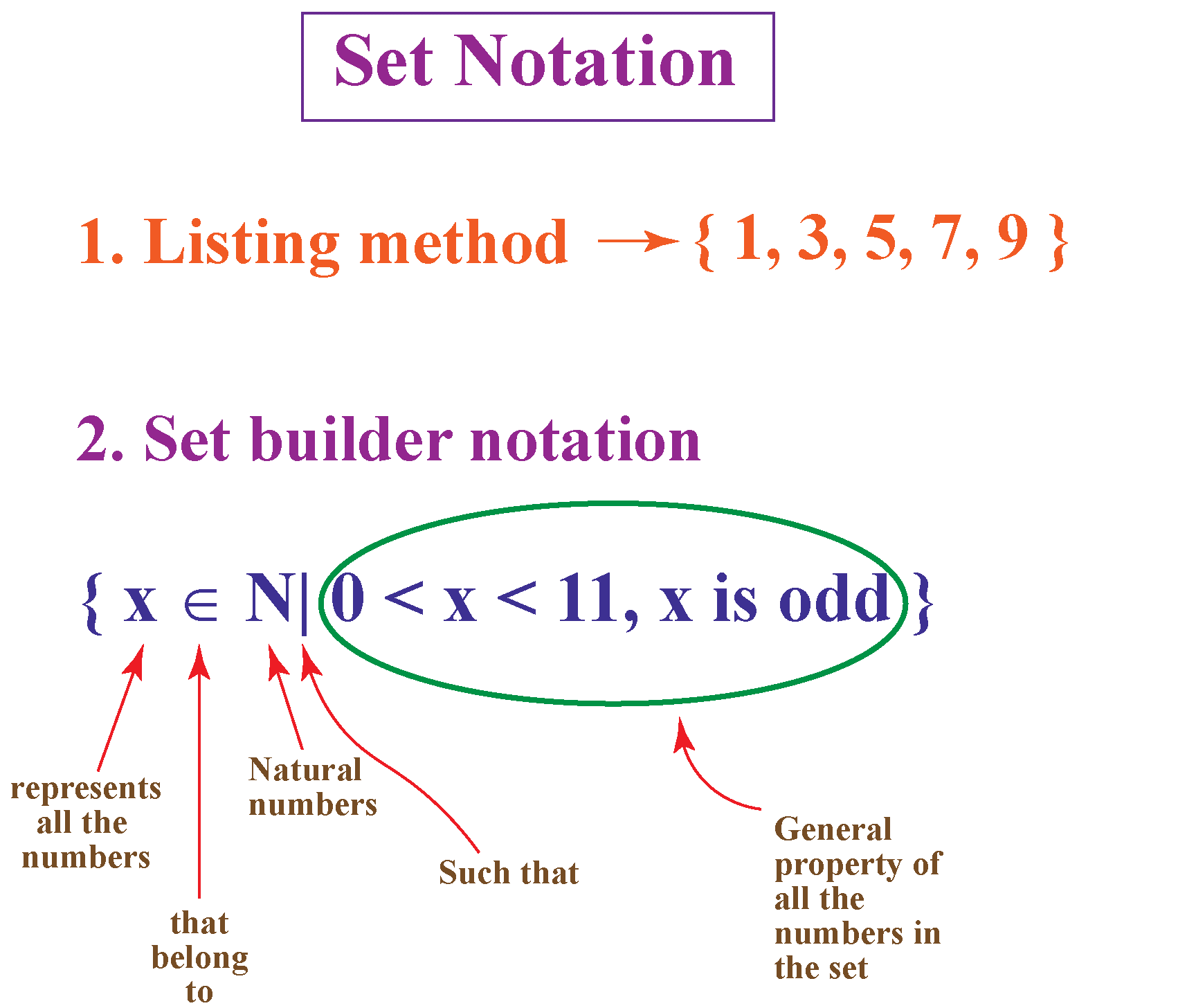
Symbols Used In Set Builder Notation
The set builder form uses various symbols to represent the elements of the set. A few of the symbols are listed as follows.
- | is read as “such that” and we usually write it immediately after the variable in the set builder form and after this symbol, the condition of the set is written.
- is read as “belongs to” and it means “is an element of”.
- is read as “does not belong to” and it means “is not an element of”.
- N represents natural numbers or all positive integers.
- Q represents rational numbers or any number that can be expressed as a fraction of integers.
- R represents real numbers or any number that isn’t imaginary.
What Is Interval Notation And Set Builder Notation Form
- In the Interval notation, the end-point values are written between brackets or parentheses. A square bracket represents that an element is included in the set, whereas a parenthesis denotes exclusion from the set.For example, (8,12]. This interval notation denotes that this set includes all real numbers between 8 and 12 where 8 is excluded and 12 is included.
- The set-builder notation is a mathematical notation for describing a set by representing its elements or explaining the properties that its members must satisfy.For example, For the given set A = , the set builder notation is A = .
Don’t Miss: Glencoe Mcgraw Hill Geometry Workbook Answers
What Are The Types Of Set Notations For Representing Elements
The two important types of set notations for representing the elements are the roster form and the set builder form. The set builder notation represents the elements of a set in the form of a sentence or mathematical expression, and the set builder form represents the elements by writing the elements distinctly. The set builder form of set notation is A = , and the roster of of the same set is A = }2, 4, 6, 8, 10}.
Euler And Venn Diagrams
ABBA
An Euler diagram is a graphical representation of a collection of sets each set is depicted as a planar region enclosed by a loop, with its elements inside. If A is a subset of B, then the region representing A is completely inside the region representing B. If two sets have no elements in common, the regions do not overlap.
A Venn diagram, in contrast, is a graphical representation of n sets in which the n loops divide the plane into 2n zones such that for each way of selecting some of the n sets , there is a zone for the elements that belong to all the selected sets and none of the others. For example, if the sets are A, B, and C, there should be a zone for the elements that are inside A and C and outside B .
Recommended Reading: What Is The Biological Importance Of Photosynthesis For The Ecosystem
Essential Features Of Cantorian Set Theory
At best, the foregoing description presents only an intuitive concept of a set. Essential features of the concept as Cantor understood it include: that a set is a grouping into a single entity of objects of any kind, and that, given an object x and a set A, exactly one of the statements x A and x A is true and the other is false. The definite relation that may or may not exist between an object and a set is called the membership relation.
A further intent of this description is conveyed by what is called the principle of extensiona set is determined by its members rather than by any particular way of describing the set. Thus, sets A and B are equal if and only if every element in A is also in B and every element in B is in A symbolically, x A implies x B and vice versa. There exists, for example, exactly one set the members of which are 2, 3, 5, and 7. It does not matter whether its members are described as prime numbers less than 10 or listed in some order between small braces, possibly .
Set Builder Notation For Domain And Range
Set builder notation is very useful for defining the domain and range of a function. In its simplest form, the domain is the set of all the values that go into a function. For Example: For the rational function, f = 2/ the domain would be all real numbers, except 1. This is because the function f would be undefined when x = 1. Thus, the domain for the above function can be expressed as . Similarly, we can represent the range of a function as well using the set builder notation.
Don’t Miss: What Are The 6 Kingdoms In Biology
Variations On Setbuilder Notation
An expressionmay be used left of the vertical line in setbuilder notation, instead of asingle variable.
Giving the type of the variable
You can use an expression on the left side of setbuilder notation to indicate the type of the variable.
Example
The unit interval $I$ could be defined as \making it clear that it is a set of real numbers rather than, say rational numbers. You can always get rid of the type expression to the left of the vertical line by complicating the defining condition, like this:\
Other expressions on the left side
Other kinds of expressions occur before the vertical line in setbuilder notation as well.
Example
The set\consists of all the squares of integers in other words its elements are 0,1,4,9,16,. This definition could be rewritten as $\left\n\in \mathrm\textm=^} \right\}$.
Example
Let $A=\left\$. Then $\left\=\left\$.
Warning
Be careful when you read such expressions.
Example
The integer $9$ is an element of the set \It is true that $9=^}$ and that $3$ is excluded by the defining condition, but it is also true that $9=^}$ and $-3$ is not an integer ruled out by the defining condition!
Sets Related To Functions
The set of all functions of a real variable, that return a real variable is denoted:\
The domain of a function is the set of all possible inputs.An input is not possible if the function is not defined for thatinput, like in the case of a divide by zero error.
The image set of a function is the set of all possible outputs of the function:\
Don’t Miss: How To Apply For Phd In Psychology
Replacement Set And Solution Set Definition
See the Replacement Set and Solution Set Definitions below.
Replacement Set: Replacement Set is the set where the values of the variable are involved in the inequation.
Solution Set: Solution Set is the set where a number is taken from the replacement set and submitted to satisfy the given inequation. The Solution Set is the subset of the Replacement Set.
Generally, we use the set of natural numbers N or the set of whole numbers W or the set of integers I or the set of real numbers R is the replacement set. When we use one of these replacement sets to prove the inequality we can get the solution set.
Examples of Replacement Set and Solution Set
Let us take the inequation to be m < 5, if: The replacement set = the set of natural numbers N, then the solution set = . If the replacement set = the set of whole numbers W, then the solution set = . If the replacement set = the set of integers Z or I, then the solution set = . The replacement set = the set of real numbers R, then the solution set represents as set-builder form i.e. .
How Do You Write Set Notation
The set notation is generally written using symbols between the sets for set operations, and certain symbols for representing some special kind of sets. The set notation for the union of sets is A U B, for the intersection of sets is A B. And the set notation for representing some important sets is the – universal set, Ø – null set.
You May Like: How To Know If You Have Chemistry With Someone
Examples On Solving Equations By Plugging In Values
Check out all the examples given below and follow the step-by-step procedure to learn the complete procedure of solving problems.
Question 1. If the replacement set is the set of integers , between 6 and 8, find the solution set of 30 6x > 2x 6.
Solution: Given that 30 6x > 2x 6Now, move the 2x on the left side of the above equation.30 6x 2x > -6Now, subtract 30 from both sides of the above equation.30 30 8x > -6 -30-8x > -36Now, divide the above equation with -8 into both sides. The inequality reverses on multiplying pr dividing both sides by -1.x < 4.5
Given that the replacement set is the set of integers between 6 and 8. Therefore, solution set =
Question 2. If the replacement set is the set of real numbers , find the solution set of 10 6x < 22.
Solution: Given that 10 6x < 22.Now, subtract 10 from both sides of the above equation.10 10 6x < 22 10 6x < 12Now, divide the above equation with -6 into both sides. The inequality reverses on multiplying pr dividing both sides by -1.-6x/-6 < 12/-6x > -2
Given that the replacement set is the set of real numbers R. Therefore, solution set =.
Question 3.List the solution set of 100 6 < 50, given that x W. Also, represent the solution set obtained on a number line.
Therefore, the solution set is . The number line is
Question 4.Solve the inequation 74 18x 16 represent the solution set on the number line. x is a whole number.
Giving Our Input And Output Elements A Name
In the interest of establishing a shorthand notation and set of vocabulary for discussing a functions key/value pairs, suppose that \ is the value that \ assigns to \. We can then write \=y\) and this can be read aloud in any of the following ways:
\ maps \ to \ The value of \ under \ is \ When \ acts on \, the resulting value is \ \ of \ equals \
Several combinations of these phrases are common, but the convention is that the word value always refers to the output or result associated with a given input.
In most cases, it is easiest to read the notation \ = y\) as \ of \ equals \.
Sometimes, we may also use the notation \, especially if we do not have a named function such as \.
For example, the function \ is a nameless function whose output is equal to the given input times 7. Note that the input set must be a set of numbers, and if we were to dive deeper into the example wed need to clarify exactly what subset of numbers we are considering.
Also Check: What Is Reproduction In Biology
Which Is The Best Form Of Set Notation For Writing A Set
The best form of set notation is the notation which helps to easily represent the elements of a set. The roster form of set notation makes a simple listing of elements of a set and is the best form of set notation. The roster form of set notation to represent a set of English alphabet vowels is A = .
Subsection111the Notion Of A Set
The term set is intuitively understood by most people to mean a collection of objects that are called elements . This concept is the starting point on which we will build more complex ideas, much as in geometry where the concepts of point and line are left undefined. Because a set is such a simple notion, you may be surprised to learn that it is one of the most difficult concepts for mathematicians to define to their own liking. For example, the description above is not a proper definition because it requires the definition of a collection. Even deeper problems arise when you consider the possibility that a set could contain itself. Although these problems are of real concern to some mathematicians, they will not be of any concern to us. Our first concern will be how to describe a set that is, how do we most conveniently describe a set and the elements that are in it? If we are going to discuss a set for any length of time, we usually give it a name in the form of a capital letter . In discussing set \ if \ is an element of \ then we will write \ On the other hand, if \ is not an element of \ we write \ The most convenient way of describing the elements of a set will vary depending on the specific set.
-
\ the positive integers, \
-
\ the natural numbers, \
-
\ the integers, \
-
\ the rational numbers
-
\ the real numbers
-
\ the complex numbers
Set-Builder Notation. Another way of describing sets is to use set-builder notation. For example, we could define the rational numbers as
Don’t Miss: How To Study Campbell Biology
How Do We Read And Write Set Notation
To read and write set notation, we need to understand how to use symbols in the following cases:
1. Denoting a Set
Conventionally, we denote a set by a capital letter and denote the elements of the set by lower-case letters.
We usually separate the elements using commas. For example, we can write the set A that contains the vowels of the English alphabet as:
We read this as the set A containing the vowels of the English alphabet.
2. Set Membership
We use the symbol is used to denote membership in a set.
Since 1 is an element of set B, we write 1B and read it as 1 is an element of set B or 1 is a member of set B.Since 6 is not an element of set B, we write 6B and read it as 6 is not an element of set B or 6 is not a member of set B.
3. Specifying Members of a Set
In the previous article on describing sets, we applied set notation in describing sets. I hope you still remember the set-builder notation!
We can describe set B above using the set-builder notation as shown below:
We read this notation as the set of all x such that x is a natural number less than or equal to 5.
4. Subsets of a set
We say that set A is a subset of set B when every element of A is also an element of B. We can also say that A is contained in B. The notation for a subset is shown below:
The symbol stands for is a subset of or is contained in. We usually read AB as A is a subset of B or A is contained in B.We use the notation below to show that A is not a subset of B:
What Is Set Builder Notation
Set-builder notation is defined as a representation or a notation that can be used to describe a set that is defined by a logical formula that simplifies to be true for every element of the set. It includes one or more than one variables. It also defines a rule about the elements which belong to the set and the elements that do not belong to the set. Let us read about different methods of writing sets. There are two methods that can be used to represent a set.
- Set builder form
The roster form or listing the individual elements of the sets, and the set builder form of representing the elements with a statement or an equation. The two methods are as follows.
Roster Form or Listing Method
In this method, we list down all the elements of a set, and they are represented inside curly brackets. Each of the elements is written only once and is separated by commas. For example, the set of letters in the word, “California” is written as A = .
Set Builder Form or Rule Method
Set builder form uses a statement or an expression to represent all the elements of a set. In this method, we do not list the elements instead, we will write the representative element using a variable followed by a vertical line or colon and write the general property of the same representative element. For example, the same set above in set builder form can be written as A = A = .
Here is another example of writing the set of odd positive integers below 10 in both forms.
Example:
Example:
You May Like: What Is Qc In Chemistry
Set Notation Or Ways To Define A Set
a. You could define a set with a verbal description: All sets above are described verbally when we say, ” The set of all bla bla bla “
b. You could make a listing of all members separated by commas with braces : A list of set 1. is written as:
c.Set-builder notation:Set 1 and set 4 can be written as and
is read, ” The set of all x such that x is a letter in the modern English alphabet.
Set-builder is an important concept in set notation. You must understand it!
We use capital letters such as A, B, and so forth to denote sets.
For example, you could let A be the set of all positive numbers less than 10.
empty set