Finding The Domain Of A Function Using A Graph
Investigating Domain And Range Using Graphs
We’re going to explore different representations of quadratic functions, including graphs, verbal descriptions, and tables. We’ll determine the domain and range of the quadratic function with these representations.
Let’s first examine graphs of quadratic functions, and learn how to determine the domain and range of a quadratic function from the graph.
A quadratic equation is any equation/function with a degree of 2 that can be written in the form y = ax2 + bx + c, where a, b, and c are real numbers, and a does not equal 0. Its graph is called a parabola. The constants a, b, and c are called the parameters of the equation. The values of a, b, and c determine the shape and position of the parabola.
The domain of a function is the set of all real values of x that will give real values for y. The range of a function is the set of all real values of y that you can get by plugging real numbers into x.
Example 1
The quadratic parent function is y = x2. The graph of this function is shown below.
Example 2
The graph of y = –x2 + 5 is shown below. Determine the domain and range of the function, and check to see if you interpreted the graph correctly.
Example 3
The graph of y = 25x2+ 4 is shown below. Determine the domain and range of this function. Drag the appropriate values into the boxes below the graph.
Domain: < x< , Range: y 0Domain: < x< , Range: y -5Domain: < x< , Range: y 2
How To Find The Domain And Range Without Using A Graph
Its always easier to determine the domain and the range of a function when we have a graph, as long as we make sure to zoom in and out to capture all the necessary details. However, graphing a function is not always possible as we may not have software or calculators to graph at any given time.
To find the domain and range without using a graph, we use what we saw earlier:
- We cannot have negative values within a square root sign.
- We cannot have zeros in the denominator of a fraction.
Don’t Miss: What Does Both Mean In Math
Domain And Range Of The Graph Of The Parabola
Example
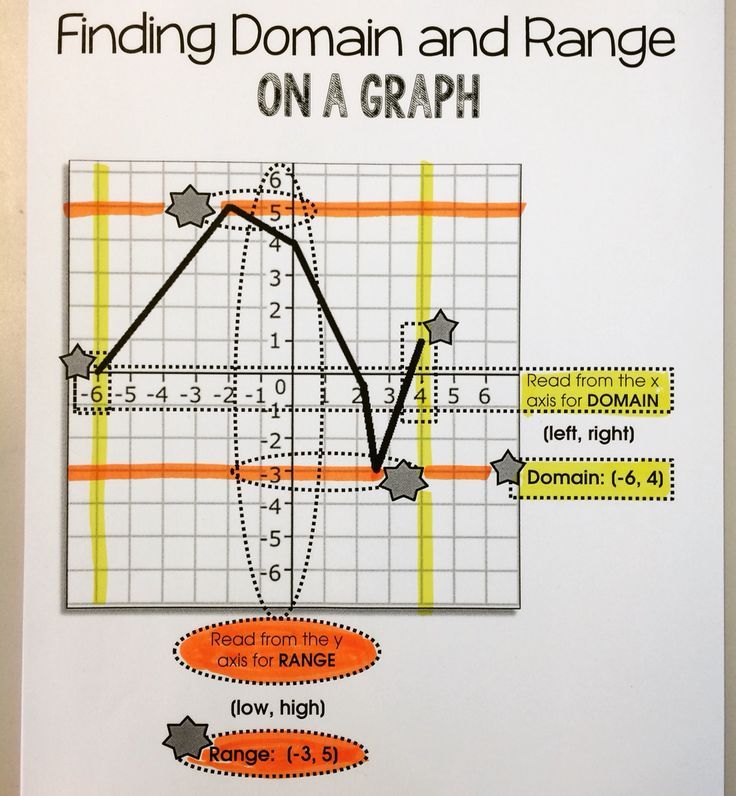
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Lets start with the domain. Remember that domain is how far the graph goes from left to right.
Start by looking at the farthest to the left this graph goes. The ???x???-value at the farthest left point is at ???x=-2???. Now continue tracing the graph until you get to the point that is the farthest to the right. The ???x???-value at this point is at ???2???. There are no breaks in the graph going from left to right which means its continuous from ???-2??? to ???2???.
Domain: ?????? also written as ???-2\leq x\leq 2???
Next, lets look at the range. Remember that the range is how far the graph goes from down to up.
Look at the furthest point down on the graph or the bottom of the graph. The ???y???-value at this point is ???y=1???. Now look at how far up the graph goes or the top of the graph. This is when ???x=-2??? or ???x=2???, but now were finding the range so we need to look at the ???y???-value of this point which is at ???y=5???. There are no breaks in the graph going from top to bottom which means its continuous.
Range: ?????? also written as ???1\leq y\leq 5???
Lets try another example of finding domain and range from a graph.
Remember that The domain is all the defined x-values, from the left to right side of the graph.
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Mcdougal Littell Algebra 2 Chapter 3 31 Section 31 Problem 73 We Can Substitute The X And Y Values Of The Ordered Pairs Into Inequality To Check If They’re Solutions Isbn 9780618595532
- Find 9780618736669 McDougalLittellAlgebra1 Assessment Book by McDougalLittell at over 30 bookstores. Buy, rent or sell.
- Buy McDougalLittellAlgebra1 Michigan Student Edition 2008 08 edition by Ron Larson for up to 90% off at Textbooks.com.
- McDougalLittellAlgebra1 2007 – AlgebraTextbook … If you use the McDougal Littell Algebra 1 textbook in class, this course is a great resource to supplement your studies. The course covers the same important algebra concepts found in the book, but… McDougalLittellAlgebra1: Online Textbook Help Course …
- In some cases, you likewise do not discover the revelation algebra 1 textbook answers mcdougal littell that you are looking for. It will no question squander the time. However below, taking into account you visit this web page, it will be hence certainly simple to acquire as with ease as download guide algebra 1 textbook answers mcdougal …
Don’t Miss: What Is The Difference Between Physical Dependence And Psychological Dependence
Determining Domain And Range
Domain:Range: parenthesis = not inclusive = open dot = < or > brackets = inclusive = closed dot = < or > u = union symbol n = overlap
- closed dot = included in domain = use brackets
- open dot = not included in domain = use parenthesis
“u” means that both pieces of the graph are part of the possible domain.
Finding The Domain Of A Function Using A Relation
You May Like: What Is Basic Research In Chemistry
Domain And Range Of A Function
The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and range is the possible output given by the function. Domain Function Range. If there exists a function f: A B such that every element of A is mapped to elements in B, then A is the domain and B is the co-domain. The image of an element ‘a’ under a relation R is given by ‘b’, where R. The range of the function is the set of images. The domain and range of a function is denoted in general as follows: Domain = and range=
The domain and range of this function f = 2x is given as domain D = , range R =
How To Find The Domain
We can determine the domain of the function by looking for the values of the independent variable , which we can use in the function. Usually, this involves avoiding values that produce a 0 in the denominator of fractions or avoiding having negative values within square roots.
Therefore, to find the domain, the important thing to remember is that:
- The denominator of a fraction cannot be zero.
- The number within a square root must be positive.
You May Like: What Does M M Mean In Chemistry
Domain And Range Of Toolkit Functions
We will now return to our set of toolkit functions to determine the domain and range of each.
For the constant function f\left=c, the domain consists of all real numbers there are no restrictions on the input. The only output value is the constant c, so the range is the set \left\ that contains this single element. In interval notation, this is written as \left, the interval that both begins and ends with c.
For the identity function f\left=x, there is no restriction on x. Both the domain and range are the set of all real numbers.
For the absolute value function f\left=|x|, there is no restriction on x. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
For the quadratic function f\left=^, the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.
For the cubic function f\left=^, the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.
For the cube root function f\left=\sqrt, the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative .
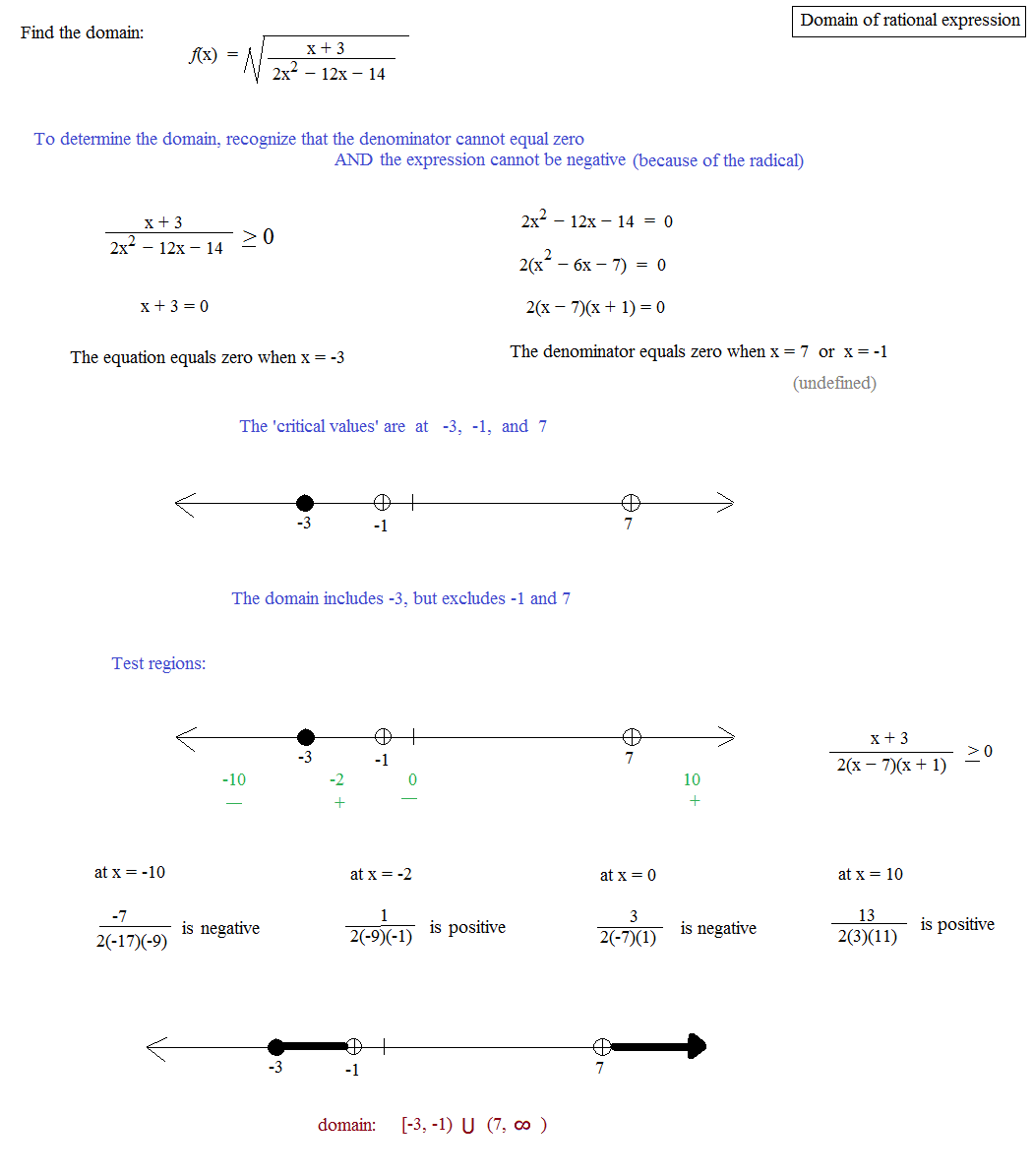
What Is An Example Of Finding The Domain And Range Of A Rational Function
-
Determine the domain and range of the following rational function:
The domain is all the values that x is allowed to take on. The only problem I have with this function is that I need to be careful not to divide by zero. So the only values that x can not take on are those which would cause division by zero. So I’ll set the denominator equal to zero and solve my domain will be everything else.
x2x 2 = 0
x = 2 or x = 1
Then the domain is “all x not equal to 1 or 2″.
The range is a bit trickier, which is why they may not ask for it. In general, though, they’ll want you to graph the function and find the range from the picture. In this case:
As you can see from my picture, the graph “covers” all y-values that is, the graph will go as low as I like, and will also go as high as I like. For any point on the y-axis, no matter how high up or low down, I can go from that point either to the right or to the left and, eventually, I’ll cross the graph. Since the graph will eventually cover all possible values of y, then:
the range is “all real numbers”.
-
Determine the domain and range of the given function:
The domain is all values that x can take on. The only problem I have with this function is that I cannot have a negative inside the square root. So I’ll set the insides greater-than-or-equal-to zero, and solve. The result will be my domain:
2x + 3 0
-
Determine the domain and range of the given function:
y = x4 + 4
Affiliate
the domain is “all x“.
The range is “all y 4″.
Don’t Miss: What Are The Levels Of Math
How Do You Write The Domain And Range
We write the domain and range of a function as the set of all the inputs a function can take and the outputs of the functions respectively. The domain and range are written from the smaller values to the larger values. The domain is written from left to right and the range is written from the top of the graph to the bottom.
Finding Domain And Range Without Using A Graph
It’s always a lot easier to work out the domain and range when reading it off the graph . However, we don’t always have access to graphing software, and sketching a graph usually requires knowing about discontinuities and so on first anyway.
As meantioned earlier, the key things to check for are:
Also Check: What Does V0 Mean In Physics
What Is An Example Of Finding The Domain And Range Of A Set Of Points
-
State the domain and range of the following relation. Is the relation a function?
The above list of points, being a relationship between certain x‘s and certain y‘s, is a relation. The domain is all the x-values, and the range is all the y-values. To give the domain and the range, I just list the values without duplication:
domain:
range:
Affiliate
While the given set of points does indeed represent a relation , the set they gave me contains two points with the same x-value: and . Since x = 2 gives me two possible destinations , then this relation cannot be a function.
And, when the relation they’ve given me is a set of points, all I need to do is check the points’ x-values if any x shows up more than once, then the relation is not a function. This relation has repeates, so it is:
not a function
Note that all I had to do to check whether the relation was a function was to look for duplicate x-values. If you find any duplicate x-values, then the different y-values mean that you do not have a function. Remember: For a relation to be a function, each x-value has to go to one, and only one, y-value.
-
State the domain and range of the following relation. Is the relation a function?
All I have to do for the domain and range parts of this exercise is list the x-values for the domain and the y-values for the range. I remember to use curly-brace set notation for each:
domain:
range:
this relation is indeed a function.
Content Continues Below
What Is The Domain And Range Of Composite Functions
Let the composite function be \. The domain and range of h are determined as follows. The domain of h is either same as f or lies within the domain of f. The range h must lie within the range of g. Let f = x2 and g = x+ 3. We know that f: X Y and g: Y Z. Then fog: X Z. f) = 2. Thus the domain and range are: domain= , range=
Also Check: What Is H2o2 In Chemistry
Finding The Domain Of A Function Defined By An Equation
In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a âholding areaâ that contains âraw materialsâ for a âfunction machineâ and the range as another âholding areaâ for the machineâs products. See Figure 2.
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, they would need to express the interval that is more than 0 and less than or equal to 100 and write (
How To Find The Domain And Range Of Rational Functions
Generally, we tend to define the domain and range of functions on real numbers, so we will do the same here. However, we will use different strategies to find the domain and range of rational functions since obtaining the graphs of these functions is not very easy. Lets consider the following rational function:
$latex f= \frac$
We observe that, for the input of -2, we obtain an output of $latex \frac$.
We know that division by zero is undefined, so the function is undefined at this point. However, any other input will have a real number output, so we conclude that the domain is all real numbers excluding -2. We can write this as:
$latex R- \$
By considering the nature of the function, we can see that any real number of outputs can be achieved with the exception of zero. This is because as x gets larger in magnitude, the output gets smaller, but the output can never equal zero. Therefore, the range of the function is:
$latex R \$
In general, we can calculate the domain of a rational function by identifying any point where the function is undefined. This means finding any point that makes the denominator equal to zero.
To find the range of a rational function, we can identify any point that cannot be reached with any input. This is generally found by considering the limits of the function as the magnitude of the inputs gets larger.
Recommended Reading: How To Find Magnitude In Physics