Properties Of Complementary Angles
Now we have already learned about the types of complementary angles. Let’s have a look at some important properties of complementary angles. The properties of complementary angles are given below:
- Two angles are said to be complementary if they add up to 90 degrees.
- They can be either adjacent or non-adjacent.
- Three or more angles cannot be complementary even if their sum is 90 degrees.
- If two angles are complementary, each angle is called “complement” or “complement angle” of the other angle.
- Two acute angles of a right-angled triangle are complementary.
How To Construct An Angle
Splashlearns vision is to transform education for K-5th grade students. It provides personalized learning for every student according to the 21st century. SplashLearn allows students to study math through a highly engaging and customized program. SplashLearn is available across all digital platforms, and more than 40 million students have used it worldwide.
To know more about angles, click here.
How To Find Complement Of An Angle
We know that the sum of two complementary angles is 90 degrees and each of them is said to be a “complement” of the other. Thus, the complement of an angle is found by subtracting it from 90 degrees. The complement of x° is 90-x°. Let’s find the complement of the angle 57°. The complement of 57° is obtained by subtracting it from 90°, i.e. 90° – 57° = 33°. Thus, the complement of 57° angle is 33°.
Also Check: What Does The Term Geography Mean
What Is A Common Vertex
A common vertex is a vertex that is shared by two angles. A vertex is the point at the intersection of any two linear constructions.
- Line segment
You can mix and match these to create vertices in many ways:
You see vertices in the corners of polygons, as central angles in circles, and when linear constructions, like parallel lines and transversals, cross.
Properties Of Adjacent Angles
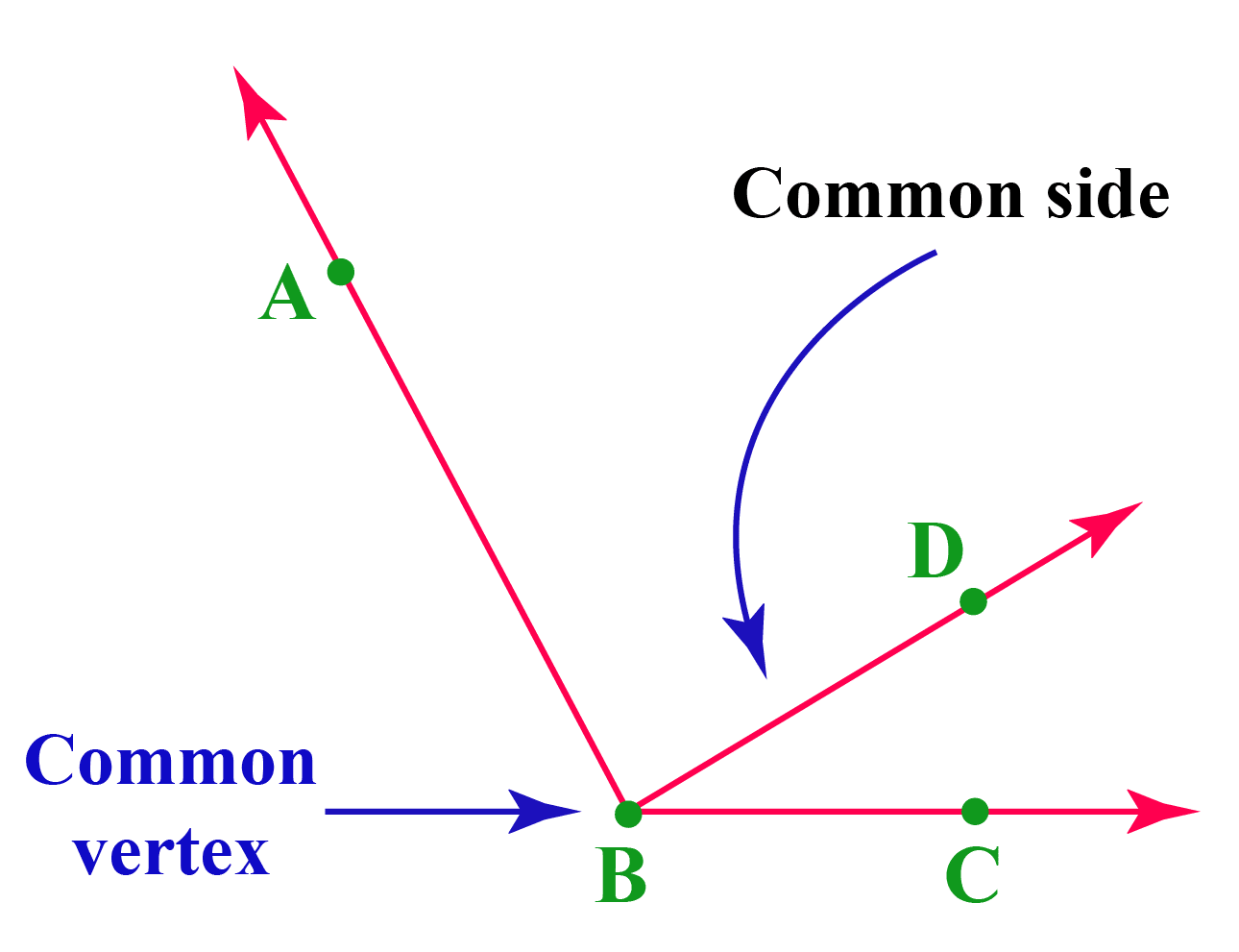
The properties of adjacent angles given below help us identify them easily.
- Adjacent angles always share a common arm.
- They share a common vertex.
- They do not overlap.
- They have a non-common arm on both sides of the common arm.
- Two adjacent angles can be supplementary or complementary based on the sum of the measures of the individual angles.
You May Like: What Is Physics Good For
When Two Lines Intersect Two Vertical Angles Are Always Congruent
This statement is known as the vertical angle theorem. Let us prove that angle 1 is congruent to angle 3.
Since angles 1 and 2 form a linear pair of angles, they are supplementary angles and
m1+m2=180°
Since angles 2 and 3 form a linear pair of angles, they are supplementary angles and
m2+m3=180°
m1+m2=m2+m3
Subtract m2 from both sides of the above equality:
m1=m3
Using the definition of congruent angles,
13
In the same way, we can prove that the remaining two vertical angles are congruent too.
What Are The Properties Of Adjacent Angles
In order to further help you visualize what adjacent angles look like, heres a quick list of their properties:
Also Check: What Is Psychoanalysis In Psychology
What Is The Difference Between Vertical And Adjacent Angles
Identifying the difference between adjacent angles and vertical angles is an important skill to master in geometry. The best way to visualize the difference between these two types of angles is to imagine two straight lines intersecting each other to form a cross.
When a cross is formed, four angles are formed. We know how to identify the adjacent angles, because they have a common side and a common vertex. But how do we identify a vertical angle? Identifying a vertical angle is equally as easy as finding an adjacent angle. Similarly to adjacent angles, a set of vertical angles will share a vertex point. However, they do not need to share a common side.
When thinking about a cross, the vertical angles are the angles that are opposite each other. This is why they are sometimes called vertically opposite angles.
English Books Relating To Adjacent Angles
adjacent anglesadjacent anglesAdjacent angles2008Adjacent anglesadjacent angles2008Adjacent AnglesADJACENT ANGLESadjacent anglesAdjacent Anglesadjacent anglesadjacentanglesadjacent anglesadjacent angles1911adjacent anglesadjacent anglesadjacent anglesadjacent2012Adjacent anglesadjacent angles2007
Don’t Miss: What Counts As Psychological Trauma
Complementary And Supplementary Angles
Supplementary and complementary angles are those angles that exist in pairs. While supplementary angles add up to 180°, complementary angles add up to 90°. These angles have numerous real-time applications, the most common being the crossroads. The following table shows the difference between supplementary and complementary angles.
The supplementary vs complementary angles table.
|
Complementary Angles |
|
|---|---|
|
Two angles are said to be complementary if they add up to 90 degrees. |
Two angles are said to be supplementary if they add up to 180 degrees. |
|
Complement of an angle x is ° |
Supplement of an angle x is ° |
Tips on Supplementary angles vs Complementary angles
Here is a short trick for you to understand the difference between supplementary angles and complementary angles.
- “S” is for “Supplementary” and “S” is for “Straight.” Hence, you can remember that two “Supplementary” angles when put together form a “Straight” angle.
- “C” is for “Complementary” and “C” is for “Corner.” Hence, you can remember that two “Complementary” angles when put together form a “Corner ” angle.
Are Adjacent Angles Complementary Or Supplementary
Adjacent angles can be both complementary and supplementary. When the two angles add up to 90° it is called adjacent complementary angles, whereas when the two angles add up to 180° it is called adjacent supplementary angles. Two adjacent supplementary angles form a linear pair.
See our Complementary and Supplementary Angles article for more details.
Read Also: What Are Dyes In Chemistry
Linear Pair Of Angles
A linear pair of angles is a pair of adjacent angles formed when two lines intersect.
The above diagram shows two intersecting lines AC and BD which form four linear pairs of angles:
- angles 1 and 2
- angles 4 and 1.
When two lines intersect, there are always four linear pairs of angles.
What is the same between a pair of adjacent angles and a linear pair of angles?
How Do You Identify Adjacent Angles
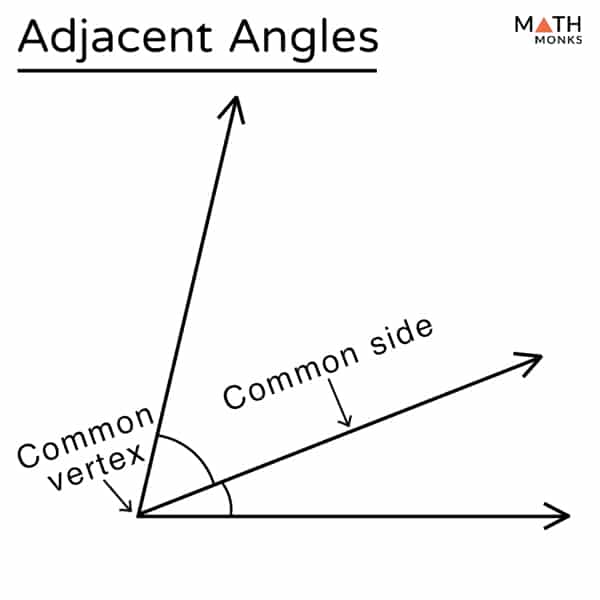
Being able to identify a common side and a common vertex is the simplest way to identify an adjacent angle. If two angles share one side and both derive from the same corner point, then they are adjacent angles.
Its important to remember that adjacent angles must have BOTH a common side and common vertex. Therefore, if you see two angles that are coming from the same corner but there is another angle in the middle, it means that they do not share any sides. This means that they are not adjacent angles as they dont share a side AND a vertex.
Identifying adjacent angles becomes easier with practice and seeing examples will help you understand what you are looking for.
Don’t Miss: Holt Algebra 2 Powerpoint Presentations
Adjacent Angles Linear Pair
Pair of adjacent angles whose measures add up to form a straight angle is known as a linear pair. The angles in a linear pair are supplementary.
Consider the following figure in which a ray
The angles POB and POA are formed at O. POB and POA are adjacent angles and they are supplementary i.e. POB + POA = AOB = 180°
POB and POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form a linear pair of angles.
What Is Different Between A Pair Of Adjacent Angles And A Linear Pair Of Angles
| Pair of adjacent angles | |
| Not necessarily form a straight angle | Form a straight angle |
| The sum of the measures is the measure of the angle formed by the two non-common arms of adjacent angles | The sum of the measures is 180° |
Supplementary angles are two angles whose measures add up to 180°.
Supplementary angles are not necessarily adjacent angles. But every two adjacent angles whose measures add up to 180° are supplementary. Using this fact, we can state that
each linear pair of angles is a pair of supplementary angles
Take an arbitrary linear pair of angles, for example, angles 1 and 2. These two angles together form the straight angle DOB. The measure of a straight angle is always 180°. Therefore, by angle addition postulate,
m1+m2=mDOB
If mDOB=180°, then
m1+m2=180°
Now, we can outline the following basic properties of a linear pair of angles:
- every linear pair of angles is a pair of adjacent angles but an arbitrary pair of adjacent angles is not necessary a linear pair of angles
- every linear pair of angles share a common vertex and a common arm between them
- every linear pair of angles always forms a straight angle
- every linear pair of angles is a pair of supplementary angles.
Note that the interior angle of the triangle and the corresponding exterior angle of the triangle together form a linear pair of angles and are always supplementary.
Don’t Miss: What Is Geography For Kids
Are Adjacent Angles Congruent
Adjacent angles are congruent only when their common side bisects their sum. This happens when:
- A right angle is bisected to from two adjacent angles each measuring 45°
- A straight angle is bisected to from two adjacent angles where each of them is a right angle measuring 90°
Solve to find the adjacent angle marked x. Given that AOB = 120° and AOC = 80°
Solution:
Definition Of Adjacent Angles
The word adjacent means next or neighboring. We can treat adjacent angles as angles that are next to each other.
Adjacent angles are a pair of angles that share a common side and vertex. Three things that need to be done to keep the angles adjacent:
- adjacent angles go in pairs
- adjacent angles share the common arm
- adjacent angles have the same vertex.
The following diagram shows two adjacent angles 1 and 2 with the common arm $\vec$ and common vertex O.
Adjacent angles never overlap
Every angle has one vertex and two arms, so it can have two possible adjacent angles, one attaching to each arm. In the diagram below, angles 2 and 3 are adjacent to angle 1: angles 1 and 2 share the common vertex O and common arm $\vec$, angles 1 and 3 share the common vertex O and common arm $\vec$.
ANGLE ADDITION POSTULATE:
The angle addition postulate states that if point B is in the interior of AOC, then
mAOB+m BOC=m AOC
This postulate can be applied to any pair of adjacent angles.
Are there any restrictions on the measures of the adjacent angles? Let us think. If two adjacent angles never overlap, then their total measure cannot be greater than the measure of a full angle. So, if angles 1 and 2 are adjacent, then
m1+m2360°
Thus, we can obtain the following combinations of adjacent angles:
We already understood what the adjacent angles are. Let us consider the following example. Will the angles AOC and AOB shown in the figure be adjacent? Why?
Also Check: How To Find Volume In Chemistry
Vertical And Adjacent Angle Pairs
When two straight lines intersect at a point, four angles are formed. Pairwise these angles are named according to their location relative to each other.
- A pair of angles opposite each other, formed by two intersecting straight lines that form an “X”-like shape, are called vertical angles or opposite angles or vertically opposite angles. They are abbreviated as vert. opp. s.
- The equality of vertically opposite angles is called the vertical angle theorem. Eudemus of Rhodes attributed the proof to Thales of Miletus. The proposition showed that since both of a pair of vertical angles are supplementary to both of the adjacent angles, the vertical angles are equal in measure. According to a historical note, when Thales visited Egypt, he observed that whenever the Egyptians drew two intersecting lines, they would measure the vertical angles to make sure that they were equal. Thales concluded that one could prove that all vertical angles are equal if one accepted some general notions such as:
- All straight angles are equal.
- Equals added to equals are equal.
- Equals subtracted from equals are equal.
AB
A transversal is a line that intersects a pair of lines, and is associated with alternate interior angles, corresponding angles, interior angles, and exterior angles.
Are Adjacent Angles Equal To 180
This is TRUE in some cases! Supplementary adjacent angles always add up to 180. This is because the two angles sit next to each other on a straight line and all angles on a straight line add up to 180.
However, if the adjacent angles are not linear pairs and another angle is in the mix, the two adjacent angles will not add up to 180.
You May Like: What Is The Concept Of Algebra
How To Find Complementary Supplementary Vertical Adjacent And Congruent Angles
When angles appear in groups of two to indicate a particular geometric property, they are called pairs of angles. In this article, you will be familiar with the types of pairs of angles.
When angles appear in groups of two to display a certain geometrical property they are called angle pairs. There is a special relationship between pairs of angles. Some of the angle pairs contain complementary angles, supplementary angles, vertical angles, and adjacent angles.
Examples Of Adjacent And Not Adjacent Angles

Determining whether two angles are adjacent or not, you should clearly remember three things that these angles should have: be a pair of angles, have a common vertex, and a common arm. It is best to learn to understand whether the angles are adjacent or not on specific examples.
EXAMPLE: In each case determine whether the angles 1 and 2 are adjacent or not.
SOLUTION: a) Pair of angles 1 and 2 share the common vertex O and common arm $\vec$, so these angles are adjacent.
b) Pair of angles 1 and 2 share the common vertex O but do not share the common arm, so these angles are not adjacent.
c) Pair of angles 1 and 2 share the common vertex O and common arm $\vec$, so these angles are adjacent.
d) Pair of angles 1 and 2 share the common arm $\vec$ but do not share the common vertex, so these angles are not adjacent.
e) Pair of angles 1 and 2 share the common vertex O and common arm $\vec$, so these angles are adjacent.
f) Pair of angles 1 and 2 share the common vertex O and common arm $\vec$, so these angles are adjacent.
g) Pair of angles 1 and 2 share the common vertex O but do not share the common arm, so these angles are not adjacent.
Read Also: How To Do Good In Physics
What Are Vertical Angles
When a pair of lines intersect, as shown in the fig. below, four angles are formed. AOD and COB are vertically opposite to each other and AOC and BOD are vertically opposite to each other. These angles are also known as vertical angles or vertically opposite angles.
Thus, when two lines intersect, two pairs of vertically opposite angles are formed i.e. AOD, COB and AOC, BOD.
According to the vertical angle theorem, in a pair of intersecting lines, the vertically opposite angles are equal.
What Are Adjacent Angles
Adjacent angles are angles that share a common vertex and a common side. The point where two sides meet and the angle is located is called the vertex. Adjacent angles can be complementary or supplementary if these angles share a vertex and a side.
Let us consider the following angles. The green angle is formed by the segments OA and OC and is represented as AOC. The pink angle is formed by the segments OC and OB and is represented as COB. This pair of angles are located close to each other and are considered adjacent.
These angles are adjacent since they have a common vertex, the vertex O. In addition, the angles also have a common side, the OC side.
Recommended Reading: How To Do Conversions In Chemistry
Adjacent Angles Sample Questions
Here are a few sample questions going over adjacent angles.
Question #1:
Which angles are not adjacent?
Answer:
C is the correct answer because a and b because although they share a common side, they have two different vertices. Therefore, they are not adjacent. Choices A, B, and D are incorrect because they all show angle pairs with common sides and a common vertex.
Question #4:
Juan is studying leaf veins and notices adjacent angles in the plant structure. He draws the diagram below and records four pairs of adjacent angles. One of Juans adjacent angle pairs is incorrect. Based on the diagram, which pair of angles is not adjacent?
GDI and WDI
Answer:
D is the correct answer because DEO and WDI are not adjacent angles. They do not share a side or a vertex. Choices A, B, and C are incorrect because these answer options list angle pairs with common sides and a common vertex.
Question #5:
Keisha and James are looking at a map of city streets and notice a lot of adjacent angles. James draws the image shown to illustrate the angles they find. Keisha points out that AOE and COD are adjacent because they share a vertex and one side. James disagrees. He says that these angles do not have a common side. Who is correct, and why?
James is correct because both angles share the same vertex but they do not have a common side.
Keisha is correct because both angles share the vertex O and line AD.
James is incorrect because AOE and COD do not have the same vertex.
Answer: