What Are The Powers Of I In Math

History Of The Notation

The term power is a mistranslation of the ancient Greek used by the Greek mathematician Euclid for the square of a line, following Hippocrates of Chios. In The Sand Reckoner, Archimedes discovered and proved the law of exponents, 10a 10b = 10a+b, necessary to manipulate powers of 10. In the 9th century, the Persian mathematician Muhammad ibn Ms al-Khwrizm used the terms for a squarethe Muslims, “like most mathematicians of those and earlier times, thought of a squared number as a depiction of an area, especially of land, hence property”and for a cube, which later Islamic mathematicians represented in mathematical notation as the letters mm and kf , respectively, by the 15th century, as seen in the work of Ab al-Hasan ibn Al al-Qalasd.

In the late 16th century, Jost Bürgi used Roman numerals for exponents.

Nicolas Chuquet used a form of exponential notation in the 15th century, which was later used by Henricus Grammateus and Michael Stifel in the 16th century. The word exponent was coined in 1544 by Michael Stifel.Samuel Jeake introduced the term indices in 1696. In the 16th century, Robert Recorde used the terms square, cube, zenzizenzic , sursolid , zenzicube , second sursolid , and zenzizenzizenzic .Biquadrate has been used to refer to the fourth power as well.

Another historical synonym,involution, is now rare and should not be confused with its more common meaning.

Combining Powers And Roots

The unit fraction notation used for roots previously may have given you the idea that roots are really the same as powers, only with a unit fraction instead of an integer as the exponent. Thus, the fractional notation is actually preferred in higher mathematics, although the root symbol is still used occasionally, especially for square roots.

How To Use The Mathematics Power Calculator

How did you solve exponents in school? The teacher simply asked you, “what is 3 raised to the power 4?” And you simply multiplied 3 by itself 4 times, right? iCalculator developed the mathematics power calculator using the same concept.

You simply need to enter the value of the base number, enter the value of how much you want it to raise to the power of, and that’s it. This online calculator will give you the right answer every time. Just make sure the value of power must be a positive integer.

If the value of the base is a negative number, the value entered in the exponent field will determine whether the answer will be a positive integer or a negative one.

For example, if you enter the base as -5, its square will be 25, its cube will be -125, -54 is 625, and so on.

Recommended Reading: Which Founding Contributors To Psychology Helped Develop Behaviorism

Bases And Exponents Of One And Zero

Any number raised to an exponent of one equals itself. So, for example, 51 = 5.

Any non-zero number raised to an exponent of zero equals one. So, for example, 50 = 1.

Zero raised to any positive exponent is still zero. So, for example, 05 = 0.

One raised to any exponent is still one. So, for example, 15 = 1.

Zero raised to an exponent of zero is not defined.

Higher Powers Of Iota

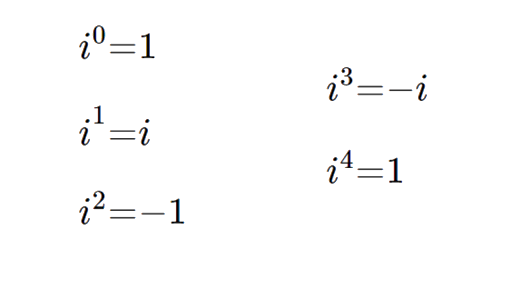
Higher powers of iota can be calculated by decomposing the higher exponents \ into smaller ones and thus evaluating the expression. Finding value if the power of iota is a larger number using the previous procedure, will take quite some time and effort. If we observe all the powers of iota and the pattern in which it repeats its values in the above equations, we can calculate the value of iota for higher powers as given below,

• Step 1: Divide the given power by 4.
• Step 2: Note the remainder for the division in Step 1, and use it as the new exponent/power of iota.
• Step 3: Calculate the value of iota for this new exponent/power using the previously known values, \ = 1 \2 = -1 and \3 = -\.

Example: Find the value of \20296.

• We first divide 20296 by 4 and find the remainder.
• The remainder is 0 .
• Thus, using the above rules, \20296 = \0 = 1
• Therefore, \20296 = 1

We just have to remember that \2 = -1 and \3 = -\. We will find some other higher powers of iota using these and the above rules.

Recommended Reading: Holt Pre Algebra Homework And Practice Workbook Answer Key

What Is Power In Mathematics

Power can be defined as a mathematical expression that can be used to represent exactly how many times a number should be used in a multiplication process. In simple words, it is an expression that describes repeated multiplication of the same given number. Power in mathematics is written as raising a number to the power of any other number.

Lets consider the following example:

3 × 3 × 3 × 3 this is equal to 81. This can also be written in this manner 34 = 81. This is an exponential notation and it simply means the number the number 3 is to be multiplied four times by itself to get the number 81 or in other words we can say 3 raised to the power of 4 or 3 raised to the 4th power gives us 81. The number 3 is known as the base number and 4 is known as the power or exponent.

How To Input Power Symbols

Choose your system to find out.

CharMap allows you to view and use all characters and symbols available in all fonts installed on your computer. You can input power signs using it.

Emoji on iOS

Character Palette

Character Palette allows you to view and use all characters and symbols, including power signs, available in all fonts installed on your computer.

Read Also: Eoc Fsa Warm Ups Algebra 1 Answers

The Interesting World Of Mathematics Power Calculator

Mathematics power, or simply exponent, is the method of multiplying a number by itself. The number in the exponential portion is the number of times you’ll need to multiply the number. The mathematics power calculator is a simple maths calculator that tells you how much a number equals in its exponential form. We are talking about squares, cubes and higher exponential powers here.

For example: if you are asked to find out the square of 5, 5², you’ll simply need to multiply 5 by itself:

Similarly, the cube of 5 will be:

These numbers may look easy to calculate, some numbers really are. Like the square of 15 , or square of 25 , or cube of 4 , or 34 .

But as the numbers go higher and the exponential power increases, finding the right answer starts becoming more and more difficult.

This is where a mathematics power calculator comes into the picture. But before we talk about this math calculator in detail let’s take a look at the exponential function in detail.

Can $n$ Be Expressed As The Sum Of $n$ Powers Of 2

New here, so this question may be a little bit messy.

Also, I don’t know if this has been asked yet, so sorry if this is a duplicate of another question.

Yesterday, I received the following question:

Prove, that for any positive integer $n$, $n!$ can be expressed as the sum of $n$ powers of $2$.

For example, $9!=2^+2^+2^+2^+2^+2^+2^+2^+2^$

I tried proving this question last night, but I just can’t seem to prove it . Any help would be greatly appreciated.

• 1$\begingroup$Hint: argue that, is a number $N$ can be written as a sum of $n$ powers of $2$, then the base $2$ expression for $N$ must contain no more than $n$ $1’s$.$\endgroup$ luluyesterday
• $\begingroup$Note: you’ll get a better response if you show some effort. How many $n’s$ did you check? Why do you imagine that this claim is true? Can you find some $N> n$ which can’t be written as the sum of $n$ powers of $2$?$\endgroup$yesterday
• 2$\begingroup$Please edit your post to show how you write $10!$ as a sum of $10$ powers of $2$.$\endgroup$yesterday
• 3$\begingroup$If one knows that $10!$ has at most $10$ bits equal to $1$, then one could repeatedly replace some terms $2^k$ with $2^+2^$ until the number of terms is finally equal to $10$.$\endgroup$

As stated by others,the number of 1 bitsin $n!$ exceeds $n$ for$n=10, 15, 16, 17, 18, 20$and,seemingly,all larger $n$.

Here is a heuristic estimate,

$n!$ has about$\dfrac$bits.Of these,about the last $n$ bitsare $0$’s,which leaves$\dfrac-n=\dfrac$.

Read Also: How Many Subfields Of Psychology Are There

Uses Of Mathematics Power In Real Life

The area of a geometric shape is in squares, while the volume is in cubes. To understand it better, suppose your bedroom is 12 feet by 12 feet. So you now simply need to know how big your room really is. So what do you do? You multiply 12 by 12, which as 12² = 144 square feet.

If we ask you how fast your mobile is, you say it has a 2 GHz processor, right? Here, GHZ means giga hertz. Do you recall how much is a Giga equal to? Giga is 109, that’s 1 followed by 9 zeros. The smaller unit, mega, is 1 followed by 6 zeros, which equals a million.

We Will Discuss Exponent Vs Power

Powers and exponents are tools to rewrite long multiplication problems easily in mathematics, especially in algebra. Algebra is known to be one of the key branches of mathematics which deals primarily with the concept of number theory. It can also be referred to as the study of mathematical symbols. You might have noticed superscript in mathematical relationships superscripts can be defined as the one that is placed above to the right of a number. This is known as an exponent and the whole expression can be called as exponentiation.

The operation involves two numbers that can be written in this way xa, where x is equal to the base number and a can be defined as the exponent. The exponent can be basically known as a superscript that is used to simplify larger mathematical problems. The whole expression is known as power and written as x to the power of a where a is any positive integer.

Don’t Miss: Who Are Paris Jackson’s Biological Parents

Powers Of Iota Calculator

Here is the “Powers of Iota Calculator”.You can enter any exponent of \ and see the result in a step-by-step manner.

Important Notes

• The value of iota is \ = 1
• The value of the square of iota is, i2 = 1
• The value of the square root of iota is, \ = 2/2 + \2/2

Tips and Tricks

• To find any power of iota, say \n, just divide n by 4 and find the remainder, r. Then just apply \n = \r. Here, you just need to remember two things \2 = 1 and \3 = \.
• To calculate the negative powers of iota, we use the rule 1/\ = \

Negative And Noninteger Powers

A base may also be raised to a negative, fractional, or decimal power. These will be covered later in this lesson

5 }=25^=5}

Note, however, that most square roots don’t yield integers, and many don’t even produce rational numbers.

Manually finding a square root

One method for manually taking square roots is to repeatedly do long division. Let’s take the square root of 10 in this example. We would start by estimating the answer. Since 32 = 9 and 42 = 16, we know the answer lies between 3 and 4. Furthermore, since 10 is only one away from 9, but is 6 away from 16, we could estimate that the answer is one-seventh of the way between 3 and 4. This won’t give an exact answer, and a seventh is ugly to work with, so let’s use a fifth, instead. This gives us 3 1/5 or 3.2 as a starting estimate.

Now do long division to divide 10 by 3.2. We get 3.125. The average of 3.2 and 3.125 is /2 = 6.325/2 = 3.1625, so that will be our next estimate.

Now do long division to divide 10 by 3.1625. We get 3.162055… . The average of 3.1625 and 3.1621 is 3.1623, so that will be our next estimate.

Now do long division to divide 10 by 3.1623. We get 3.162255…

So, this method can be repeated to get the desired level of accuracy. The actual square root of 10 is 3.16227766…

Note that calculators or computers are used for most square root calculations, but knowing how to manually calculate a square root can be quite useful when no calculator is available.

You May Like: Geometry Segment Addition Postulate Worksheet

Properties Of An Exponential Function

The properties of the exponential function are better understood by the operations we can do on powers:

Exponent Example 1

When multiplying two or more powers with the same base simply, you simply need to add the exponents:

Exponent Example 2

A power raised to a power multiplies the exponents:

Exponent Example 3

Raising the power of a product increases the powers of the involved numbers by the same power.

Exponent Example 4

Dividing powers with the same base leads to subtraction of the exponents.

xa/xb2³/2²

Exponent Example 5

A non zero bases with exponent = 0 is always yields 1 as answer.

Negative exponents can be written in fractional form.

1/x1/21/4

Exponent Example 6

Exponents with fractional are the roots.

and so on

Powers Of I When N < 0

i-1 = 1/i = / = i/i2 = i/-1 = -i

i-2 = 1/i2 = 1/-1 = -1

i-3 = 1/i3 = 1/-i = / = i/1 = i

i-4 = 1/i4 = 1/1 = 1

i-7 = i

i-8 = 1

Notice the pattern -i, -1, i, 1, … repeats after the first four complex numbers. In general, if n is an integer smaller than zero, the value of in can be found by dividing n by 4 and examining the remainder.Did you make the following observations?

• For i-4 and i-8, the remainder is 0 when we divide 4 and 8 by 4.
• For i-3 and i-7, the remainder is -3 when we divide -3 and -7 by 4.
• For i-2 and i-6, the remainder is -2 when we divide -2 and -6 by 4.
• For i-1 and i-5, the remainder is -1 when we divide 1 and 5 by 4.

Let n < 0 and R is the remainder

If R = -1, in = -i

If R = -2, in = -1

If R = -3, in = i

If R = 0, in = 1

Also Check: Do You Capitalize Bachelor’s Degree In Psychology

Questions To Be Solved:

Question 1) Find the value of the 25.

Solution) To find the value of 25We need to multiply the base that is equal to 2 , and the exponent tells us how many times the number needs to be multiplied by itself.

25 = 2 × 2 × 2 × 2 × 2 equals 32.

Question 1)What is an Exponent and What is Power in Math?

Answer) Lets know about exponent and power.An expression that represents repeated multiplication of the same factor is known as a power. For example, 52 here, the number 5 is known as the base, and the number 2 is known as the exponent. The exponent is 2 that correspond to the number of times the base is used as a factor.

Question 2) What is Power in Math?

Answer) The power of a number basically defines how many times to use the number in the multiplication process. It is written as a small number to the right and above the base number whose power we need to find.

Question 3) What are the 7 Laws of Exponents?

Answer)Here are the seven laws of exponents :

• Multiplying the powers that have the same Base.

• Dividing Powers having the same Base.

• Power of a Power.

• Multiplying Powers that have the same Exponents.

• The concept of Negative Exponents.

• Power with Exponent equal to Zero.

• Fractional Exponent.

A Few Examples Showing How To Find The Powers Of I

Example #1:

67 divided 4 gives a remainder of 3. Since n is positive, i67 = -i

Example #2:

-67 divided 4 gives a remainder of -3. Since n is negative, i-67 = i

Example #3:

36 divided 4 gives a remainder of 0. Since n is positive, i36 = 1

Example #4:

Also Check: Eoc Fsa Warm Ups Algebra 1 Answers

Efficient Computation With Integer Exponents

Computing bn using iterated multiplication requires n 1 multiplication operations, but it can be computed more efficiently than that, as illustrated by the following example. To compute 2100, apply Horner’s rule to the exponent 100 written in binary:

100

by using exponentiation by squaring, where n denotes the number of 1 in the binary representation of n. For some exponents , the number of multiplications can be further reduced by computing and using the minimal addition-chain exponentiation. Finding the minimal sequence of multiplications for bn is a difficult problem, for which no efficient algorithms are currently known , but many reasonably efficient heuristic algorithms are available. However, in practical computations, exponentiation by squaring is efficient enough, and much more easy to implement.

Power Of Maths Of Powers

Exponentiation is a mathematical operation, written as b, involving two numbers, the base b and the exponent n. When n is a positive integer, exponentiation corresponds to repeated multiplication in other words, is product of a number b multiplied by itself n times.

The exponent is usually shown as a superscript to the right of the base. The exponentiation b can be read as: b raised to the n-th power, b raised to the power of n, or b raised by the exponent of n, most briefly as b to the n. Some exponents have their own pronunciation: for example, b² is usually read as b squared and b³ as b cubed.

The power b can be defined also when n is a negative integer, for nonzero b. No natural extension to all real b and n exists, but when the base b is a positive real number, b can be defined for all real and even complex exponents n via the exponential function ex.

Also this index symbols are used in chemistry to denote chemical elements .

Also Check: The Branch Of Chemistry That Involves The Study Of Substances