A Deliciously Simple Application Of Algebra In Real Life
Imagine that youre going to a big holiday feast, and youre in charge of buying the groceries and cooking the meal. You have decided that the main course for the meal will be a nice juicy turkey. As you look around the supermarket to choose a turkey, you are disappointed to find only one remains.
The weight on the package says that the turkey weighs 18 lbs. How can you determine how many people this turkey will feed so that nobody goes hungry at dinner?
As a general rule of thumb, you need approximately 1.5 lbs of turkey for each person. You pull out a piece of paper and a pen and write down the following algebraic equation:
What you have just performed is one of the most basic, real-life uses for algebra. A variable value, x, represents the number of people who can be fed with an 18 pound turkey if we assume that 1.5 lbs are needed for each person. In this case, we have solved for x to determine that our 18 pound turkey can feed a total of 12 people.
While this example may seem trivial, it illustrates that we often use algebra without realizing it. Thanks to experience, we often do these quick computations in our heads, but at the root of what we are solving is an algebraic equation. Now, look ahead to the next part of our holiday dinner preparation for another application of algebra that you can use in real life.
What Are The Applications Of Linear Equations In Real Life
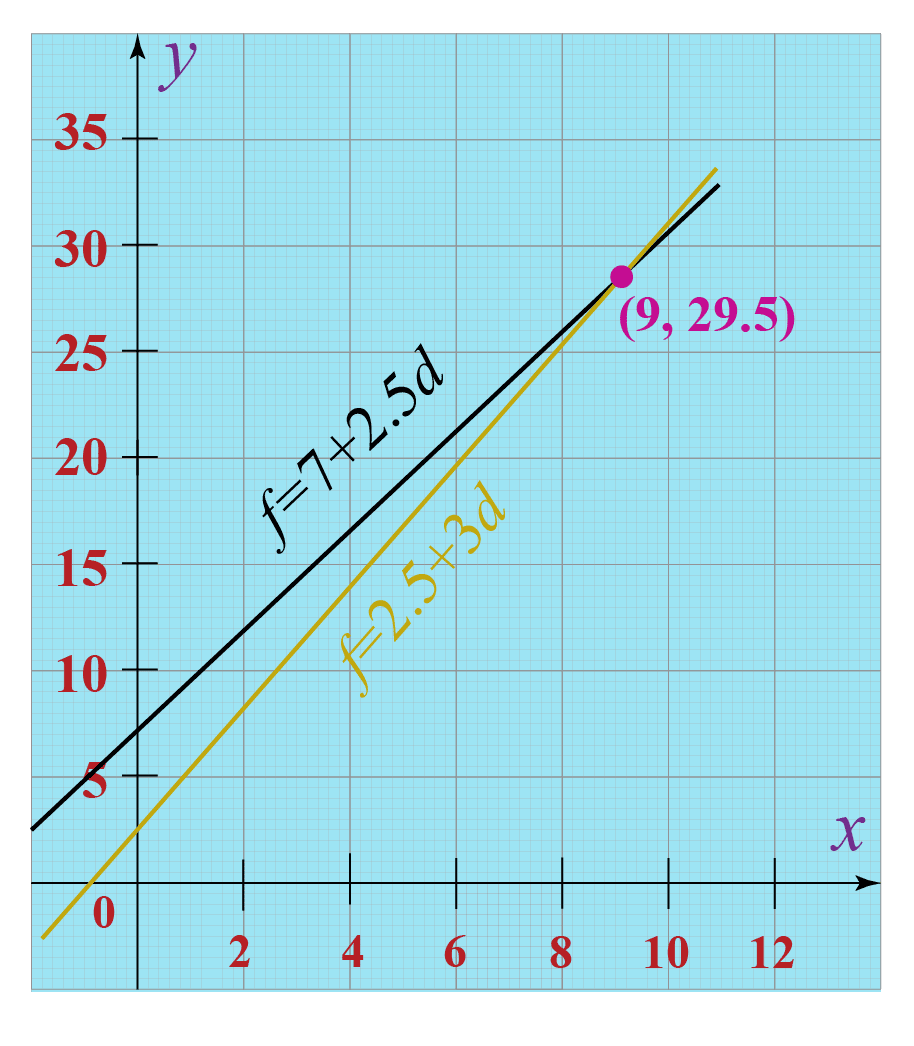
In real-life situations where there is an unknown quantity or identity, the use of linear equations comes into play, for example, figuring out income over time, calculating mileage rates, or predicting profit. Most of the time mental calculations are used in some real-life situations without drawing a line graph.
Why Study Linear Algebra
I have come across this question way too many times. Why should you spend time learning Linear Algebra when you can simply import a package in Python and build your model? Its a fair question. So, let me present my point of view regarding this.
I consider Linear Algebra as one of the foundational blocks of Data Science. You cannot build a skyscraper without a strong foundation, can you? Think of this scenario:
You want to reduce the dimensions of your data using Principal Component Analysis . How would you decide how many Principal Components to preserve if you did not know how it would affect your data? Clearly, you need to know the mechanics of the algorithm to make this decision.
With an understanding of Linear Algebra, you will be able to develop a better intuition for machine learning and deep learning algorithms and not treat them as black boxes. This would allow you to choose proper hyperparameters and develop a better model.
You would also be able to code algorithms from scratch and make your own variations to them as well. Isnt this why we love data science in the first place? The ability to experiment and play around with our models? Consider linear algebra as the key to unlock a whole new world.
Don’t Miss: How To Learn Psychology Fast
Algebra In Computer Programming
As we have seen, algebra is about recognising general patterns. Rather than looking at the two equations 3x+1=5 and 6x+2=3 as two completely different things, Algebra sees them as being examples of the same general equation ax+b=c. Specific numbers have been replaced by symbols.
Computer programming languages, like C++ or Java, work along similar lines. Inside the computer, a character in a computer game is nothing but a string of symbols. The programmer has to know how to present the character in this way. Moreover, he or she only has a limited number of commands to tell the computer what to do with this string. Computer programming is all about representing a specific context, like a game, by abstract symbols. A small set of abstract rules is used to make the symbols interact in the right way. Doing this requires algebra.
An Algebraic Recipe For Tasty Results
You have finished your grocery trip and returned home from the supermarket to prepare the big feast. The turkey is stuffed and ready to go in the oven, and the potatoes are cooked, but you still have to make your famous homemade cranberry sauce.
As you are about to begin following your recipe, you notice that it only makes enough cranberry sauce for four servingsbut you will have a total of twelve people to feed. Before the anxiety kicks in you rely on math to save the day.
You know that you need to make a larger batch, which means using more of each ingredient. Glancing over your recipe, you notice that it calls for 3 cups of cranberries to be used for four servings. So, how do you determine how much you need to use to feed all twelve people?
Using a pen, you jot down the following on the back of the recipe card:
This time you decided to write an equation using two variables. The variable y represents the total number of cups of cranberries you should use in your recipe. It is the target variable in this equation.
The variable x represents the number of diners that you are trying to feed. The beauty of this equation is that any time you need to cook your recipe for more than four people, you can always change the value of x to the number of people for whom you are cooking. This will allow you to determine how many cups of cranberries to use on that occasion.
Cool, huh?
Read Also: How To Calculate Standard Deviation Chemistry
Support Vector Machine Classification
Ah yes, support vector machines. One of the most common classification algorithms that regularly produces impressive results. It is an application of the concept of Vector Spaces in Linear Algebra.
Support Vector Machine, or SVM, is a discriminative classifier that works by finding a decision surface. It is a supervised machine learning algorithm.
In this algorithm, we plot each data item as a point in an n-dimensional space with the value of each feature being the value of a particular coordinate. Then, we perform classification by finding the hyperplane that differentiates the two classes very well i.e. with the maximum margin, which is C is this case.
A hyperplane is a subspace whose dimensions are one less than its corresponding vector space, so it would be a straight line for a 2D vector space, a 2D plane for a 3D vector space and so on. Again Vector Norm is used to calculate the margin.
But what if the data is not linearly separable like the case below?
Our intuition says that the decision surface has to be a circle or an ellipse, right? But how do you find it? Here, the concept of Kernel Transformations comes into play. The idea of transformation from one space to another is very common in Linear Algebra.
Lets introduce a variable z = x² + y². This is how the data looks if we plot it along the z and x-axes:
What Are The Top Applications Of Linear Algebra
A spy detective game is one of my favorite games in my childhood. And I think you are not an exception who never play this game. In my childhood age, I always imagined how detectives decode secret messages? And I was always curious to know about it.
When I grow up, I am able to find out the method to decode the message. What is that? Well, it is one of the applications of linear algebra called Cryptography. Below, I have explained the exciting applications of linear algebra in detail. So, lets move to the details of one more concept of mathematics.
You May Like: What Math Do You Take In 11th Grade
Definition Of Linear Equations
An equation with degree 1 is considered a linear equation. In other words, a linear equation is an equation that is written for two different variables. This equation will be a linear combination of these two variables, and a constant can be present. The standard form is ax + by = c, where a and b are coefficients, x and y are variables, and c is the constant. A linear equation can also be plotted on a graph where it is a straight line. The image below shows a few examples of linear equations.
Application Of Linear Algebra In Real Life: Where It Is Used
Linear algebra is widely used in the fields of Math, Science, and Engineering. Basically, it plays a vital role in determining unknown quantities. Below are some of the linear algebra concepts that are used in real life.
- Linear Algebra is used to check the distribution of microwave energy in a microwave oven.
- It is used to create ranking algorithms in search engines such as Google, Yahoo, etc.
- Used to recover the codes that have been tampered with during processing or transmission.
- Used for space studies.
- It is used for projecting a three-dimensional view into a two-dimensional plane, handled by linear maps.
- Used to examine the digital signals and encode or decode them. These can be the signals of audio or video.
- It is used to optimize in the field of linear programming.
- Used to check the energy levels of atoms.
Suppose you are interested in computer science and want to know where linear algebra applications are used in computer science. We listed six linear algebra applications that are used in computer science.
Recommended Reading: What Does The Word Psychology Mean
Practical Applications Of Algebra
Home/Practical Applications of Algebra
Its easy to think of algebra as an abstract notion that has no use in real life. Understanding the history and the practical applications of algebra that are put into use every day might make you see it a little differently.
The main idea behind algebra is to replace numbers by symbols. This makes things a lot simpler: instead of saying Im looking for a number so that when I multiply it by 7 and add 3 I get 24, you simply write 7x+3=24, where x is the unknown number.
Algebra is a huge area in mathematics, and there are many mathematicians who spend their time thinking about what you can do with collections of abstract symbols. In real life, however, algebra merges into all other areas as a tool. Whenever life throws a maths problem at you, for example when you have to solve an equation or work out a geometrical problem, algebra is usually the best way to attack it. The equations you are learning about now are the ones that youre most likely to come across in everyday life. This means that knowing how to solve them is very useful. If youre planning to go into computer programming, however, the algebra youll need is more complicated and nows the time to make sure you get the basics.
Did you know? The word algebra comes from the ancient Arabic word al jebr, which means the reunion of broken parts.
Convolution And Image Processing
2D Convolution is a very important operation in image processing. It consists of the below steps:
The function can seem a bit complex but its widely used for performing various image processing operations like sharpening and blurring the images and edge detection. We just need to know the right kernel for the task we are trying to accomplish. Here are a few kernels you can use:
You can download the image I used and try these image processing operations for yourself using the code and the kernels above. Also, try this Computer Vision tutorial on Image Segmentation techniques!
Amazing, right? This is by far my most favorite application of Linear Algebra in Data Science.
Now that you are acquainted with the basics of Computer Vision, it is time to start your Computer Vision journey with 16 awesome OpenCV functions. We also have a comprehensive course on Computer Vision using Deep Learning in which you can work on real-life Computer Vision case studies!
You May Like: What Is The Difference Between Organic And Inorganic Chemistry
Applications Of Linear Equations
Applications of linear equations are used by people on a daily basis even without using a line graph because the situations faced by them might have an unknown quantity that can be represented as a linear equation such as calculating mileage rates, income over time, etc. The important aspect here is the four main arithmetic operations – addition, subtraction, multiplication, and division. Let us learn more about the applications of linear equations in this article and solve some real-life examples.
| 1. |
| FAQs on Application of Linear Equations |
Real World Applications Of Linear Algebra

I watched 3blue1brown’s excellent series of linear algebra, which shows the visual intuition behind linear algebra and matrices. In short, matrices are a compact representation of linear transformations applied to a vector space, so that all points in that space are stretched and skewed from their starting position in some way.
I understand that much. But it’s far too abstract for me because I cannot think of a single real-world problem that is modeled like this.
When I google around for real-world applications of matrices, I run into unhelpful descriptions like this that basically give you a table of values and treats the table like an excel spreadsheet. In the linked article, the author gives an example of how to compute sales of pies by representing flavors pies as rows, and quantity of pies sold as columns. This is not intuitive because I can’t mentally connect sales of pie to linear algebra. How could you possibly model sales of pie as a set of linear transformations of vector space?
I’d like to connect the theory of linear algebra to something concrete and practical.
What is a real-world application of linear algebra and matrices? More specifically, how is that real-world application modeled as a set of linear transformations applied to vector space?
Recommended Reading: What Does The Backwards E Mean In Math
Forming An Equation To Find The Unknown
Translating verbal descriptions into algebraic expressions is an essential initial step in solving word problems. So lets see another real-life example in the form of a puzzle.
Detailed Solution:
Our first supposition is that Uma buys at least one ball of each kind. Now lets say she buys x footballs, y cricket balls, and z table-tennis balls.
The question requires x + y + z = 100
It also requires 15 x + 1y + z/4 = 100 Since we have 3 variables but only 2 equations well have to use the trial and error method to get at the solution.
Lets vary x the number of footballs and see what we get:
Suppose x = 1, then
y + z =99 and y + z/ 4 = 83z/4 = 14 3z = 56 z = 56/3 which is not a whole number.
Trying for x = 2 also fails and now
If x = 3, then z = 97 and y + z / 4 = 55 3z/4 =42 3z= 168 z = 168/3 = 56 which is a whole number!
And if z = 56 then y = 97 – z = 97 – 56 = 41
So the set of balls Uma buys is
What Is The Application Of Linear Equations
The main objective for the applications of linear equations or linear systems is to solve various problems using two variables where one is known and the other is unknown, also dependent on the first. Some of these applications of linear equations are:
- Geometry problems by using two variables.
- Money problems by using two variables
- A mixture of problems by using two variables.
- Distance-Rate-Time problems by using two variables.
- Application of linear equation in business and economics
Recommended Reading: Specialized Body Geometry Xct Lock On
Dataset And Data Files
In machine learning, you fit a model on a dataset.
This is the table-like set of numbers where each row represents an observation and each column represents a feature of the observation.
For example, below is a snippet of the Iris flowers dataset:
| 1 | 5.0,3.6,1.4,0.2,Iris-setosa |
This data is in fact a matrix: a key data structure in linear algebra.
Further, when you split the data into inputs and outputs to fit a supervised machine learning model, such as the measurements and the flower species, you have a matrix and a vector . The vector is another key data structure in linear algebra.
Each row has the same length, i.e. the same number of columns, therefore we can say that the data is vectorized where rows can be provided to a model one at a time or in a batch and the model can be pre-configured to expect rows of a fixed width.
For help loading data files as NumPy arrays, see the tutorial:
Read The Problem Again
You must read the problem carefully to understand what is given, what kind of application of linear system it is, and what is to be found. If required read it as many times as it takes.It is imperative for you to completely understand and identify all the given information and what you are being asked to find. Be mindful as at times one word can completely change how the application of a linear system is worked.
Read Also: What Are All The Laws Of Physics
Examples Of Linear Algebra In Machine Learning
Jason BrownleeLinear AlgebraTweet
Linear algebra is a sub-field of mathematics concerned with vectors, matrices, and linear transforms.
It is a key foundation to the field of machine learning, from notations used to describe the operation of algorithms to the implementation of algorithms in code.
Although linear algebra is integral to the field of machine learning, the tight relationship is often left unexplained or explained using abstract concepts such as vector spaces or specific matrix operations.
In this post, you will discover 10 common examples of machine learning that you may be familiar with that use, require and are really best understood using linear algebra.
After reading this post, you will know:
- The use of linear algebra structures when working with data, such as tabular datasets and images.
- Linear algebra concepts when working with data preparation, such as one hot encoding and dimensionality reduction.
- The ingrained use of linear algebra notation and methods in sub-fields such as deep learning, natural language processing, and recommender systems.
Kick-start your project with my new book Linear Algebra for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Lets get started.
10 Examples of Linear Algebra in Machine LearningPhoto by j. Barbosa, some rights reserved.