Mean Average Vs Average Deviation From The Mean
Calculating the mean average is also a crucial step in determining what the average deviation from the mean is. The mean average is simply the sum of all values included in the data set, divided by the total number of values. Calculating the mean average helps you determine the deviation from the mean by calculating the difference between the mean and each value. Next, divide the sum of all previously calculated values by the number of deviations added together and the result is the average deviation from the mean.
How To Calculate Relative Standard Deviation
The formula for calculating the relative standard deviation is as follows:
/x = relative standard deviation
In this formula, S stands for the standard deviation and x stands for the mean of the data being used. Following are the steps to calculate this formula to determine the relative standard deviation:
Calculate the mean of the numbers in the data you are working with.
Subtract the mean from each number in the data to determine the deviation for each number.
Square the deviations for each number.
Add together the squared deviations.
Divide the sum of the squared deviations by the total number of values used to get the variance.
Find the square root of the variance to get the standard deviation of the data.
Multiply the standard deviation by 100 and then divide this number by the mean.
Related:
Examples Of Relative Standard Deviation Formula
Lets take an example to understand the calculation of Relative Standard Deviation in a better manner.
Relative Standard Deviation Formula Example #1
Calculate the Relative Standard Deviation for the following set of numbers: 48, 52, 56, 60 where the standard deviation is 2.48.
Solution:
Sample Mean is calculated as:
- Sample Mean = /4
- Sample Mean = 216/4
Relative Standard Deviation is calculated using the formula given below
Relative Standard Deviation = / x¯
- Relative Standard Deviation = / 54
- Relative Standard Deviation = / 54
- Relative Standard Deviation = 4.6
Thus, the RSD for the above number is 4.6.
Relative Standard Deviation Formula Example #2
Calculate the Relative Standard Deviation for the following set of numbers: 10, 20, 30, 40 and 50 where the standard deviation is 10.
Solution:
Sample Mean is calculated as:
- Sample Mean = /5
- Sample Mean = 150 / 5
Relative Standard Deviation is calculated using the formula given below
Relative Standard Deviation = / x¯
- Relative Standard Deviation = / 30
- Relative Standard Deviation = 1000 / 30
- Relative Standard Deviation = 33.33
Thus, the RSD for the above number is 33.33.
Relative Standard Deviation Formula Example #3
Calculate the Relative Standard Deviation for the following set of numbers: 8, 20, 40 and 60 where the standard deviation is 5.
Solution:
Sample Mean is calculated as:
- Sample Mean = /4
- Sample Mean = 128 / 4
Relative Standard Deviation = / x¯
Read Also: Holt Geometry Lesson 4.5 Practice B Answers
Uncertainty In The Regression Analysis
As shown in Figure 5.4.4, because indeterminate errors in the signal, the regression line may not pass through the exact center of each data point. The cumulative deviation of our data from the regression linethat is, the total residual erroris proportional to the uncertainty in the regression. We call this uncertainty the standard deviation about the regression, sr, which is equal to
where yi is the ith experimental value, and \ is the corresponding value predicted by the regression line in Equation \ref. Note that the denominator of Equation \ref indicates that our regression analysis has n 2 degrees of freedomwe lose two degree of freedom because we use two parameters, the slope and the y-intercept, to calculate \.
Did you notice the similarity between the standard deviation about the regression and the standard deviation for a sample /04%3A_Evaluating_Analytical_Data/4.04%3A_The_Distribution_of_Measurements_and_Results#equation4.4.1″ rel=”nofollow”> Equation 4.1.1)?
A more useful representation of the uncertainty in our regression analysis is to consider the effect of indeterminate errors on the slope, b1, and the y-intercept, b0, which we express as standard deviations.
We use these standard deviations to establish confidence intervals for the expected slope, \, and the expected y-intercept, \
Example 5.4.2
| 60.562 | 0.0202 |
Finally, the 95% confidence intervals , 4 degrees of freedom) for the slope and y-intercept are
When To Calculate Standard Deviation
You can use standard deviation for more than just statistics, probability theory, chemistry and mathematics. It has real-world applications in many fields, especially in finance. Standard deviation is one of the fundamental measurements of risk that analysts, portfolio managers and investment advisors use. Here are some examples:
-
You can use the standard deviation formula to find the annual rate of return of an investment or study an investment’s historical volatility.
-
Investment firms can use standard deviation to report on their mutual funds and other products as it shows whether the return on funds is deviating from normal expectation.
-
You can use it to predict performance trends or help with trading strategies in the market.
-
It can help portfolio managers differentiate between aggressive growth funds which have a high standard deviation or more stable growth funds with a lower standard deviation.
In real-world applications, you rarely solve the standard deviation formula with pencil and paper. Calculating the formula by hand is very time-consuming and there is a high risk of making a mistake. With today’s technology, you usually solve standard deviation calculations through computer programs or spreadsheets.
However, when you’re first learning about the standard deviation formula, it helps to solve a few problems by hand to gain insight and understanding about how the formula actually works.
Related:
The formula for calculating standard deviation is:
Such that:
Related:
Read Also: What Does Competition Mean In Biology
How A Linear Regression Works
To understand the logic of a linear regression consider the example shown in Figure 5.4.2, which shows three data points and two possible straight-lines that might reasonably explain the data. How do we decide how well these straight-lines fit the data, and how do we determine the best straight-line?
Lets focus on the solid line in Figure 5.4.2. The equation for this line is
where b0 and b1 are estimates for the y-intercept and the slope, and \ is the predicted value of y for any value of x. Because we assume that all uncertainty is the result of indeterminate errors in y, the difference between y and \ for each value of x is the residual error, r, in our mathematical model.
Figure 5.4.3 shows the residual errors for the three data points. The smaller the total residual error, R, which we define as
the better the fit between the straight-line and the data. In a linear regression analysis, we seek values of b0 and b1 that give the smallest total residual error.
The reason for squaring the individual residual errors is to prevent a positive residual error from canceling out a negative residual error. You have seen this before in the equations for the sample and population standard deviations. You also can see from this equation why a linear regression is sometimes called the method of least squares.
yy yi
The Equation Defining Variance
Now that you know how the summation operator works, you can understand the equation that defines the population variance :
The variance , is defined as the sum of the squared distances of each term in the distribution from the mean , divided by the number of terms in the distribution .
There’s a more efficient way to calculate the standard deviation for a group of numbers, shown in the following equation:
You take the sum of the squares of the terms in the distribution, and divide by the number of terms in the distribution . From this, you subtract the square of the mean . It’s a lot less work to calculate the standard deviation this way.
It’s easy to prove to yourself that the two equations are equivalent. Start with the definition for the variance . Expand the expression for squaring the distance of a term from the mean .
Now separate the individual terms of the equation . In the final term, the sum of 2/N, taken N times, is just N2/N.
Next, we can simplify the second and third terms in Equation 3. In the second term, you can see that X/N is just another way of writing , the average of the terms. So the second term simplifies to 22 . In the third term, N/N is equal to 1, so the third term simplifies to 2 .
Finally, from Equation 4, you can see that the second and third terms can be combined, giving us the result we were trying to prove in Equation 5.
As an example, let’s go back to the two distributions we started our discussion with:
| Data Set | |
|---|---|
| 11.00 | 3.32 |
Don’t Miss: Figure Ground Psychology
Exercise : Calculating The Mean
The sample mean is the average value for a finite set of replicatemeasurements on a sample. It provides an estimate of the population mean for the sample using the specific measurement method. The sample mean, denoted , is calculated using the formula:
Suppose we use atomic absorbance spectroscopy to measure the total sodium content a can of soup we perform themeasurement on five separate portions of the soup, obtainingthe results 108.6, 104.2, 96.1, 99.6, and 102.2 mg. What isthe mean value for the sodium content of the can of soup?
You have already used the relevant Excel functionsfor this calculation in . Set up a new worksheet and calculatethe mean value, using the COUNT and SUM functions, and the AVERAGEfunction you should get the same values.
Skip to Reporting Results
Standard Deviation V/s Variance
The list of standard deviation v/s variance is given below in tabulated from
|
Variance |
Standard Deviation |
|
Variance is simply stated as the numerical value, which mentions how variable in the observation are. |
Standard deviation is simply stated as the observations that are measured through a given data set. |
|
Variance is nothing but average taken out from the standard deviation. |
Standard deviation is stated as the root of the mean square deviation. |
|
It is defined using squared units |
It is defined using the same units of the data available |
|
Mathematically, variance is denoted as |
Mathematically, variance is denoted as |
|
Variance is the accurate estimate of the individuals spread out in the group |
Variance is the accurate estimate of the observations in a given data set. |
Also Check: Geometry Segment Addition Postulate Worksheet
Why Is Standard Deviation A Useful Measure Of Variability
Although there are simpler ways to calculate variability, the standard deviation formula weighs unevenly spread out samples more than evenly spread samples. A higher standard deviation tells you that the distribution is not only more spread out, but also more unevenly spread out.
This means it gives you a better idea of your datas variability than simpler measures, such as the mean absolute deviation .
The MAD is similar to standard deviation but easier to calculate. First, you express each deviation from the mean in absolute values by converting them into positive numbers . Then, you calculate the mean of these absolute deviations.
Unlike the standard deviation, you dont have to calculate squares or square roots of numbers for the MAD. However, for that reason, it gives you a less precise measure of variability.
Lets take two samples with the same central tendency but different amounts of variability. Sample B is more variable than Sample A.
| Values |
|---|
Different Ways To Calculate Standard Deviation
There are two main ways to calculate standard deviation: population standard deviation and sample standard deviation. If you collect data from all members of a population or set, you apply the population standard deviation. If you take data that represents a sample of a larger population, you apply the sample standard deviation formula. The equations/calculations are nearly the same with two exceptions: for the population standard deviation, the variance is divided by the number of data points , while for the sample standard deviation, it’s divided by the number of data points minus one .
You May Like: What Is The Formula Of Volume In Physics
What Does Standard Deviation Tell You
Standard deviation is a useful measure of spread fornormal distributions.
In normal distributions, data is symmetrically distributed with no skew. Most values cluster around a central region, with values tapering off as they go further away from the center. The standard deviation tells you how spread out from the center of the distribution your data is on average.
Many scientific variables follow normal distributions, including height, standardized test scores, or job satisfaction ratings. When you have the standard deviations of different samples, you can compare their distributions using statistical tests to make inferences about the larger populations they came from.
The mean ratings are the same for each group its the value on the x-axis when the curve is at its peak. However, their standard deviations differ from each other.
The standard deviation reflects the dispersion of the distribution. The curve with the lowest standard deviation has a high peak and a small spread, while the curve with the highest standard deviation is more flat and widespread.
How Can The Standard Deviation For A Set Of Experimental Value Be Interpreted In Terms Of Precision

I have read from many websites that the sample standard deviation can be used to measure the precision of experimental values. I understand that the lower the standard deviation the better, as it would mean that the values are close together . But what standard deviation is small enough to be considered precise?
As an example, in a redox titration experiment I obtained titrant values of $16.3$, $16.4$, $16.5$ and $\pu$.
From these four measurements, I thus calculate an average of $\pu$ and a standard deviation of $\pu$. The uncertainty of the burette is $\pm\,\pu$.
From this standard deviation, would this experiment’s results be considered precise?
If not, why not, and how would I interpret it?
Is there a better method for quantifying precision?
- MithoronApr 29 ’17 at 14:08
- $\begingroup$One std dev corresponds to obtaining data that is within $\approx 68 $ % of the mean, this means that $32$ %of the time results will be outside this range by random chance and you seem to have observed one of these. If you calc 2 std dev then your values should be outside this range only $\approx 5$ % of the time. Of course your results may not be accurate but that is a different matter.$\endgroup$
But what standard deviation is small enough to be considered precise?
“Sufficiently precise,” ironically enough, is something that can’t really be defined precisely in general terms.
In other words, a level of precision that is perfectly fine in one context might be unacceptably low in others.
Recommended Reading: Which Founding Contributors To Psychology Helped Develop Behaviorism
Explore Our Science Videos
| How Do Viruses React To Soap?How Do Viruses React To Soap? | Magic Triangles – Fun Math Puzzles with Increasing DifficultyMagic Triangles – Fun Math Puzzles with Increasing Difficulty | Popsicle Stick Chain Reaction -STEM activityPopsicle Stick Chain Reaction -STEM activity |
You can find this page online at: https://www.sciencebuddies.org/science-fair-projects/science-fair/variance-and-standard-deviation
You may print and distribute up to 200 copies of this document annually, at no charge, for personal and classroom educational use. When printing this document, you may NOT modify it in any way. For any other use, please contact Science Buddies.
The Uncertainty Of The Slope:
The slope of the regression line is obviously important, as it determinesthe sensitivity of the calibration function that is, the rateat which the signal changes with concentration. The higher theslope, the easier it is to distinguish between concentrations which areclose to one another. The uncertainty in the slope is expressed as thestandard error of the slope, sb,and is calculated in terms of the standard error of the regression as:
The corresponding confidence interval for the slope is calculated usingthe t-statistic for degress of freedom as:
b±tn2sb
Skip to Using Excels functions
Don’t Miss: Kendall Hunt Middle School Math Answer Key
Mean Standard Deviation And Standard Uncertainty
Brief summary: the lecture explains calculation of mean and standard deviation . Illustrates again the 68% probability of s. Explains how the standard uncertainty of repeatability u can be estimated as standard deviation of parallel measurement results. Stresses the importance of standard uncertainty as the key parameter in carrying out uncertainty calculations: uncertainties corresponding to different sources and to different distribution functions are converted to standard uncertainties when uncertainty calculations are performed.
Mean, standard deviation and standard uncertainty
One of the most common approaches for improving the reliability of measurements is making replicate measurements of the same quantity. In such a case very often the measurement result is presented as the mean value of the replicate measurements. In the case of pipetting n times with the same pipette volumes V1, V2, , Vn are obtained and the mean value Vm is calculated as follows:
As explained in section 3.1, the mean value calculated this way is an estimate of the true mean value .
The scatter of values obtained from repeated measurements is characterized by standard deviation of pipetted volumes, which for the same case of pipetting is calculated as follows:
Two important interpretations of the standard deviation:
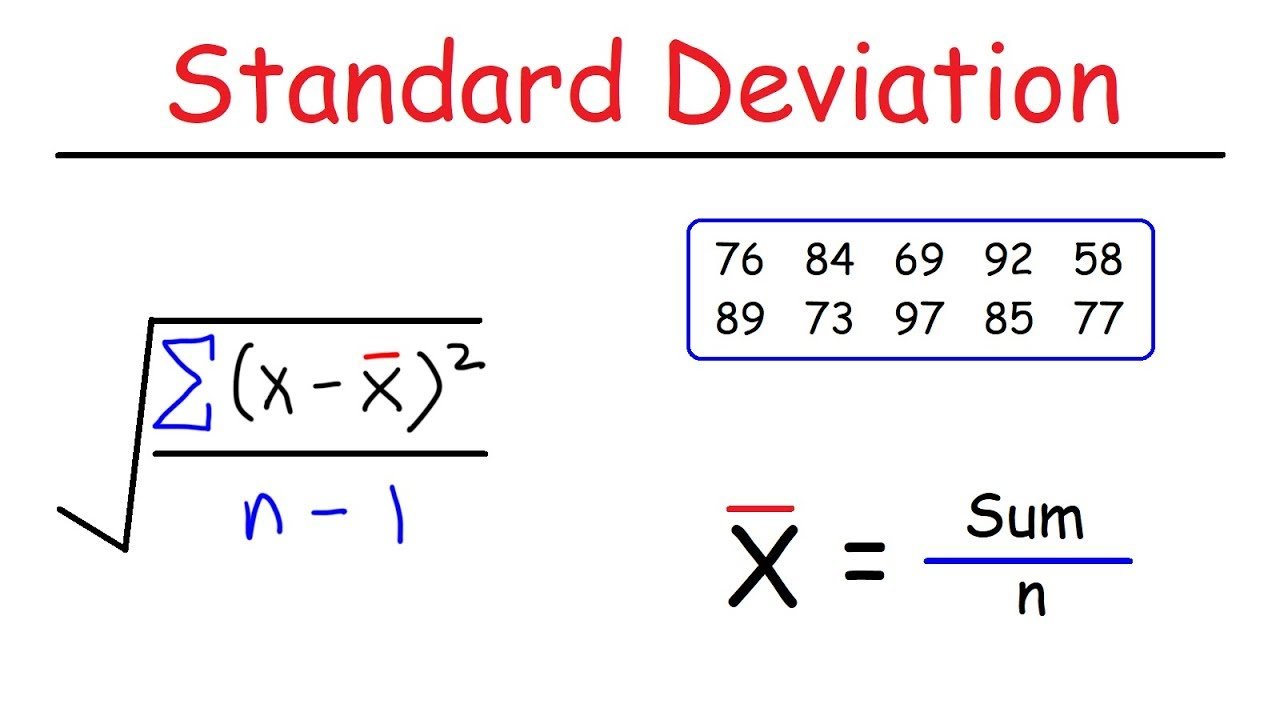
Calculating The Standard Deviation
Also Check: Who Are Paris Jackson’s Biological Parents